6 Begriffsbildung
Lernziele
- Sie kennen Kriterien für das Verständnis von Begriffen.
- Sie kennen Wege der Begriffseinführung und wählen diese zielgerichtet aus – auch abhängig von der didaktischen Funktion des jeweiligen Begriffs.
- Sie können geeignete Beispiele und Gegenbeispiele auswählen und anordnen, um Begriffsbildungsprozesse zu unterstützen.
Material
6.1 Begriffsverständnis
6.1.1 Begriffsbegriff
Angenommen, Sie würden eine Schülerin oder einen Schüler auffordern, den Begriff Quader zu definieren. Die Person äußert sich, dass es sich dabei um ein Viereck mit vier gleich langen Seiten und vier rechten Winkeln handelt. Wie würden Sie da als Lehrkraft reagieren? Hat diese Person tatsächlich nicht verstanden, was ein Quader ist? Was können Sie als Lehrkraft tun, um herauszufinden, welche Wissens- oder Verständnislücken vorliegen?
Derartige Gedanken werden Ihren Schulalltag prägen, denn die Bildung von Begriffen ist eine der wesentlichen Aufgaben des Mathematikunterrichts. Nach Zech (1998, S. 165) bietet sich folgende Definition an:
Definition 6.1 (Begriff) Man spricht allgemein von einem »Begriff«, wenn eine Anzahl von Objekten oder Ereignissen aufgrund gewisser übereinstimmender Merkmale mit einem gemeinsamen Namen belegt wird (vgl. Weinert 1974, S. 664).
Damit werden zwei Dimensionen von Begriffen sichtbar, nämlich der Bezeichner und das Bezeichnete. Während der Bezeichner das Wort bzw. der Name ist, mit dem das zu betrachtende Objekt oder Ereignis belegt wird, ist das Bezeichnete die Idee hinter dem Objekt, also das Gefüge an übereinstimmenden Merkmalen. Weder Bezeichner noch Bezeichnetes sind jedoch das Objekt oder Ereignis selbst. Äquivalente, und auch in den Sprachwissenschaften bedeutsame Bezeichnungen sind Signifikant für den Bezeichner und Signifikat für das Bezeichnete (vgl. auch Rembowski, 2015, S. 13 ff.; Wikipedia, 2021d, 2021c).
Im obigen Beispiel hat die Schülerin oder der Schüler für den Bezeichner Quader das Bezeichnete eines Quadrates definiert. Es kann sich hier also durchaus um eine Wortverwechslung handeln, die nicht zwingend mit einem inhaltlichen Fehlverständnis einhergehen muss.
Was heißt es nun, einen Begriff verstanden zu haben?
Zunächst einmal müssen »Kenntnisse, Vorstellungen über sowie Fähigkeiten im Umgang mit Merkmalen oder Eigenschaften eines Begriffs und deren Beziehungen untereinander« entwickelt werden (Weigand, 2015, S. 264). Dies wird als ein Verständnis über den Begriffsinhalt bezeichnet, zu dem natürlich auch die Definition des Begriffs gehört, aber eben nicht ausschließlich.
Weiterhin ist der Begriffsumfang Bestandteil des Begriffsverständnisses, was heißt, »einen Überblick über die Gesamtheit aller Objekte [zu] erhalten, die unter einem Begriff zusammengefasst werden« (Weigand, 2015, S. 264).
Hinzu kommt das Begriffsnetz, über das »Beziehungen des Begriffs zu anderen Begriffen« aufgezeigt werden können (Weigand, 2015, S. 264).
Wenn dann noch »Kenntnisse hinsichtlich der Anwendungen des Begriffs sowie Fähigkeiten im Umgang mit dem Begriff« ausgeprägt sind und die Schülerinnen und Schüler in der Lage sind, die »Begriffsbildungen kritisch zu reflektieren« (Weigand, 2015, S. 264), kann von einem weitreichenden Begriffsverständnis gesprochen werden.
6.1.2 Verständnistiefe
Die verschiedenen mathematischen Begriffe haben eine unterschiedliche Bedeutsamkeit innerhalb der mathematischen Bildung in der Schule (und darüber hinaus). So ist offenbar der Zahlbegriff derart fundamental und vielschichtig, dass er in allen Jahrgängen in verschiedenen Ausprägungen trägt (und nicht umsonst eine der fünf Leitideen nach den Bildungsstandards ist), während beispielsweise der Begriff Bruchstrich als Bestandteil eines Bruches kaum weitergehende Bedeutung hat und vielmehr einer erleichternden Kommunikation dient.
Vollrath (o. J., S. 2) unterscheidet dahingehend in verschiedene Didaktische Funktionen eines Begriffs und formuliert (Hervorhebungen im Original kursiv, hier fett):
»Begriffe können als Leitbegriffe eines Themenstrangs dienen, der sich über mehrere Jahrgangsstufen erstreckt. Man denke etwa an die Begriffe Zahl, Funktion, Figur oder Abbildung.
Begriffe können als Schlüsselbegriffe eine Unterrichtssequenz strukturieren. Das kann etwa der Begriff des Bruchs für die Bruchrechnung sein, der Begriff der proportionalen Zuordnung für die Schlussrechnung, der Begriff der Symmetrie für die Lehre von den Dreiecken und Vierecken.
Ein Begriff kann zentraler Begriff einer Unterrichtseinheit sein, der in ihr erarbeitet wird. Hier ist an Begriffe zu denken wie Primzahl, Quadratwurzel, Potenzfunktion, gleichseitiges Dreieck, Kreis, Tangente, Scherung, Prisma usw.
Schließlich dienen Begriffe als Arbeitsbegriffe dazu, beim Arbeiten bestimmte Sachverhalte griffig zu formulieren, um über sie sprechen zu können. Hier ist an Begriffe wie Zähler, Nenner, Klammer, Grundzahl, Hochzahl, Ecke, Seite, Kante usw. zu denken.«
Offensichtlich benötigen Begriffe mit einer langfristigeren Perspektive, wie Leitbegriffe, auch ein tieferes Verständnis und damit mehr Aufmerksamkeit bei der Begriffsbildung. Vollrath (1984, S. 215 f.) schlägt für Leitbegriffe daher einen mehrstufigen Aufbau der Verständnistiefe vor (vgl. auch Lechner, o. J., S. 10):
Intuitives Begriffsverständnis (Begriff als Phänomen)
Die Schülerinnen und Schüler entwickeln eine grundlegende Idee des Begriffs, ohne dass er für sie schon mathematisch greifbar sein muss. Der Begriff wird bspw. als Phänomen in der Umwelt erkannt oder sich ihm durch Handlungserfahrungen genähert. Diese Stufe ist also auch wesentlich, um Grundvorstellungen aufzubauen.
Inhaltliches Begriffsverständnis (Begriff als Träger von Eigenschaften)
Der Begriff wird über seine Eigenschaften erfasst, ohne dass diese explizit benannt werden müssten. So können z. B. Vorschulkinder Dreiecke und Vierecke erkennen, ohne dass ihnen eine mathematische Definition bewusst wäre. Auf dieser Stufe ist es auch schon möglich, Probleme mithilfe der Begriffseigenschaften zu lösen (z. B. das Einsetzen entsprechender Figuren in geometrische Puzzle), ohne dass der Bezeichner des Begriffs zwingend verwendet werden muss.
Integriertes Begriffsverständnis (Begriff als Teil eines Begriffsnetzes)
Der Begriff kann nun in Zusammenhang mit anderen Begriffen eines Begriffsnetzes gebracht werden. So können bspw. Gemeinsamkeiten und Unterschiede verwandter Begriffe identifiziert werden.
Formales Begriffsverständnis (Begriff als formales Objekt)
Auf dieser Stufe ist für den Begriff eine mathematische Definion bekannt. So können Eigenschaften des Begriffs erläutert werden und es kann begründet werden, ob und warum einzelne Objekte zum Begriff gehören oder nicht. Der Begriff kann somit auch in Beweisen genutzt werden.
Strukturelles Begriffsverständnis (Begriff als strukturierbares Objekt)
Der Begriff kann nun als Strukturobjekt aufgefasst werden, so dass er selbst wieder Anlass für mathematische Untersuchungen ist. Beim Funktionsbegriff heißt dies z. B., dass Verknüpfungen zwischen Funktionen hergestellt werden oder Darstellungsformen miteinander in Bezug gebracht werden können.
Zumindest die ersten drei Stufen sind auch für kurz- und mittelfristig auszuprägende Begriffe relevant (vgl. Weigand, 2015, S. 273 ff.).
6.2 Wege zum Begriff
6.2.1 Arten der Begriffseinführung
Die Einführung von Begriffen kann stets als Wechselspiel zwischen Beispielen/Gegenbeispielen und der Begriffsfestlegung aufgefasst werden. Je nachdem, in welcher Richtung und Qualität dieser Zusammenhang erbracht wird, spricht man von einer ostensiven, induktiven oder deduktiven Begriffseinführung (siehe Abbildung 6.1).
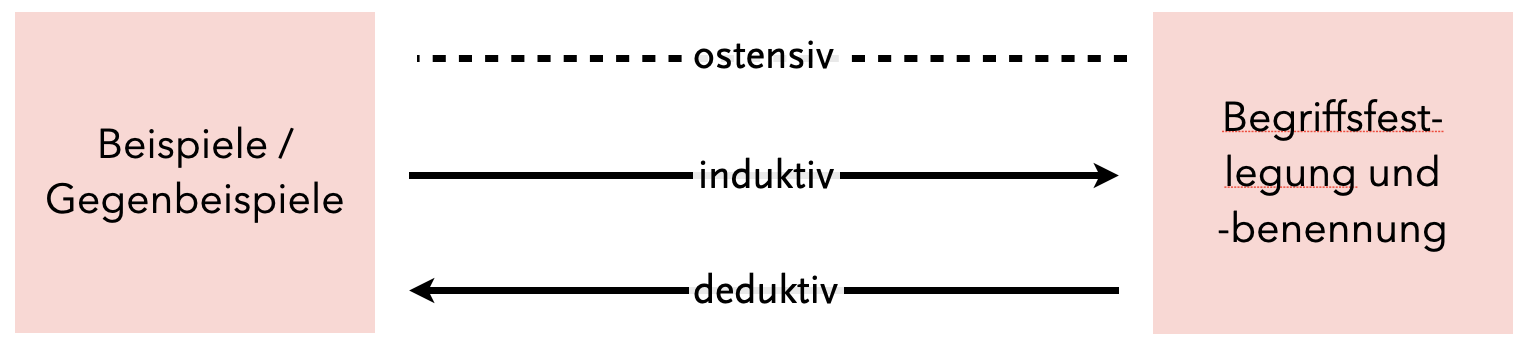
Abb. 6.1: Möglichkeiten der Begriffseinführung
Neben diesen drei Grundformen gibt es auch noch Abwandlungen und Abweichungen, wie z. B. das Aufsteigen vom Abstrakten zum Kokreten (siehe Abschnitt 7.1.3) oder die Operative Genese in der Geometrie (siehe Abschnitt 6.4).
6.2.1.1 Ostensive Begriffseinführung
Bei der ostensiven Begriffseinführung wird das Lernen eines Begriffs als Erfassen der Gestalt als einprägsames Ganzes angenommen. Das heißt, der Begriff wird gar nicht formal definiert, sondern nur über Beispiele dargestellt. Dies wird insbesondere bei Arbeitsbegriffen so gehandhabt (z. B. Bruchstrich) oder bei der Begriffseinführung in der Grundschule, wenn deren Gestalt leicht eingänglich ist (z. B. Kreis).
Dabei muss jedoch die wahrgenommene Gestalt dem Wesentlichen des Begriffs entsprechen und der Gestalteindruck ist häufig abhängig von der Lage. Es ist also darauf zu achten, nicht ausschließlich Spezialfälle zu präsentieren, die dann zu einer Untergeneralisierung des Begriffs führen. Werden z. B. zwei zueinenander senkrechte Strecken präsentiert, sollten diese also nicht gleich lang sein, sich nicht in der Mitte schneiden und auch nicht parallel zu den Tafel-/Blatt-/Bildschirmrändern ausgerichtet sein (siehe Abbildung 6.2).
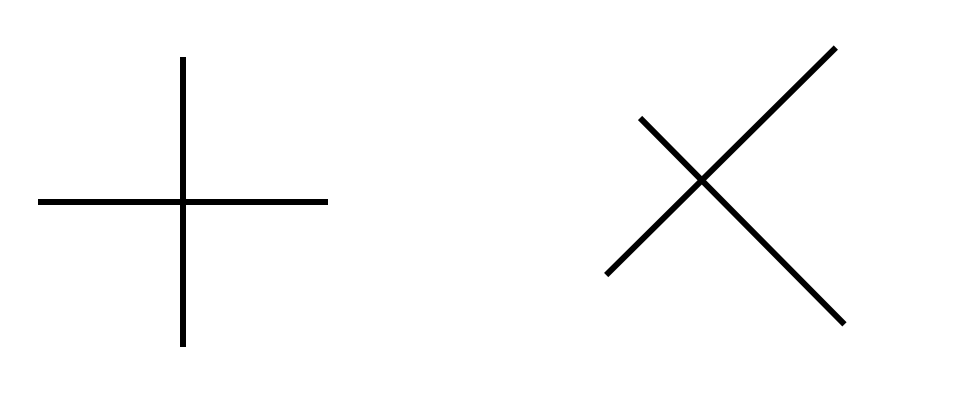
Abb. 6.2: Ungeeignete und geeignete ostensive Darstellung des Begriffs senkrecht zueinander
6.2.1.2 Induktive Begriffseinführung
Bei der induktiven Begriffseinführung wird zunächst eine Vielzahl an Beispielen präsentiert. Aus diesen heraus wird dann das Wesentliche des Begriffs extrahiert. Dafür werden die Objekte zunächst beschrieben und anschließend gemeinsame Eigenschaften entdeckt. Dies kann passieren, indem die ungeordneten Beispiele nach Merkmalen sortieren werden oder bereits in Teilmengen aufgeteilt präsentiert werden. Daran wird nun der Begriffsinhalt herausgearbeitet.
Dieses Vorgehen ist relativ natürlich, da es auch der Begriffsbildung im Vorschulalter bzw. im Alltag entspricht. Allerdings benötigt es sehr viel Zeit. Hinzu kommt, dass das Erkennen der gemeinsamen Merkmale in der Unterrichtssituation nicht selten zu einem Ostereiersuchen verfällt, indem die Lehrkraft so lange nachfragt, bis die gewünschte Eigenschaft gefunden wird. Oder noch kritischer formuliert: »Die Lernenden jedoch haben noch keine Ahnung von diesem Wesen und können sie auch nicht gewinnen, da sie keinerlei Mittel dafür besitzen.« (Giest & Lompscher, 2004)
Beim Einsatz der induktiven Begriffseinführung müssen also insbesondere geeignete Impulsfragen im Vorhinein bedacht werden, um die Schülerinnen und Schüler durch gezielte Fragestellungen das Wesentliche des Begriffs entdecken lassen zu können.
6.2.1.3 Deduktive Begriffseinführung
Die deduktive Begriffseinführung geht den Weg von der Definition zu den Beispielen. Dieses Vorgehen ist das übliche in der Hochschulmathematik und sollte – um zum Beispiel wissenschaftspropädeutisch tätig zu sein – auch im Schulunterricht schon vermittelt werden.
Typische Lernhandlungen im Zusammenhang mit deduktiver Begriffseinführung sind das Identifizieren (d. h. anhand existierender Objekte die Begriffszugehörigkeit entscheiden) und Realisieren (d. h. Herstellen) von Repräsentanten9 des Begriffs und das Begründen der Begriffszugehörigkeit.
Typische Impulsfragen für den Unterricht, um die deduktive Begriffseinführung nach Gabe der Definition zu unterstützen, können sein:
- Ist das ein …?
- Stelle ein … her.
- Welche Teile der Definition sind nicht erfüllt?
- Was muss an dem … verändert werden, damit es ein … ist?
- Wie prüft man, ob das ein … ist?
- Warum entsteht ein …, wenn man das so und so herstellt?
6.2.2 Beispiele und Gegenbeispiele
Unabhängig davon, auf welche Art und Weise man Begriffe einführt, ist stets ein Zusammenspiel aus Beispielen, Gegenbeispielen und verbalen Erläuterungen notwendig – und das in allen Altersklassen! Bei entsprechenden Verbalisierungen sind ggf. weniger Beispiele/Gegenbeispiele nötig, da damit das Wesen des Begriffs besser herausgearbeitet werden kann (Zech, 1998, S. 260).
Bei der Auswahl von Beispielen und Gegenbeispielen bieten sich das Variationsprinzip und das Kontrastprinzip an. Die folgenden Überlegungen stammen hauptsächlich von Zech (1998, S. 260 ff.).
6.2.2.1 Variationsprinzip
Beispiele sollten breit variiert werden, es darf nicht zu einer Untergeneralisierung kommen. Im Alltag als Gegenbeispiele empfundene Beispiele müssen mit angebracht werden. Wichtig erscheinende irrelevante Merkmale sollten mindestens einmal variiert werden.
Für den Rechtecktbegriff kann dies eine Variation in Größe, Seitenverhältnis, Ausrichtung und Farbe, aber auch die Präsentation von Spezialfällen (z. B. eines Quadrates) bedeuten (siehe Abbildung 6.3).
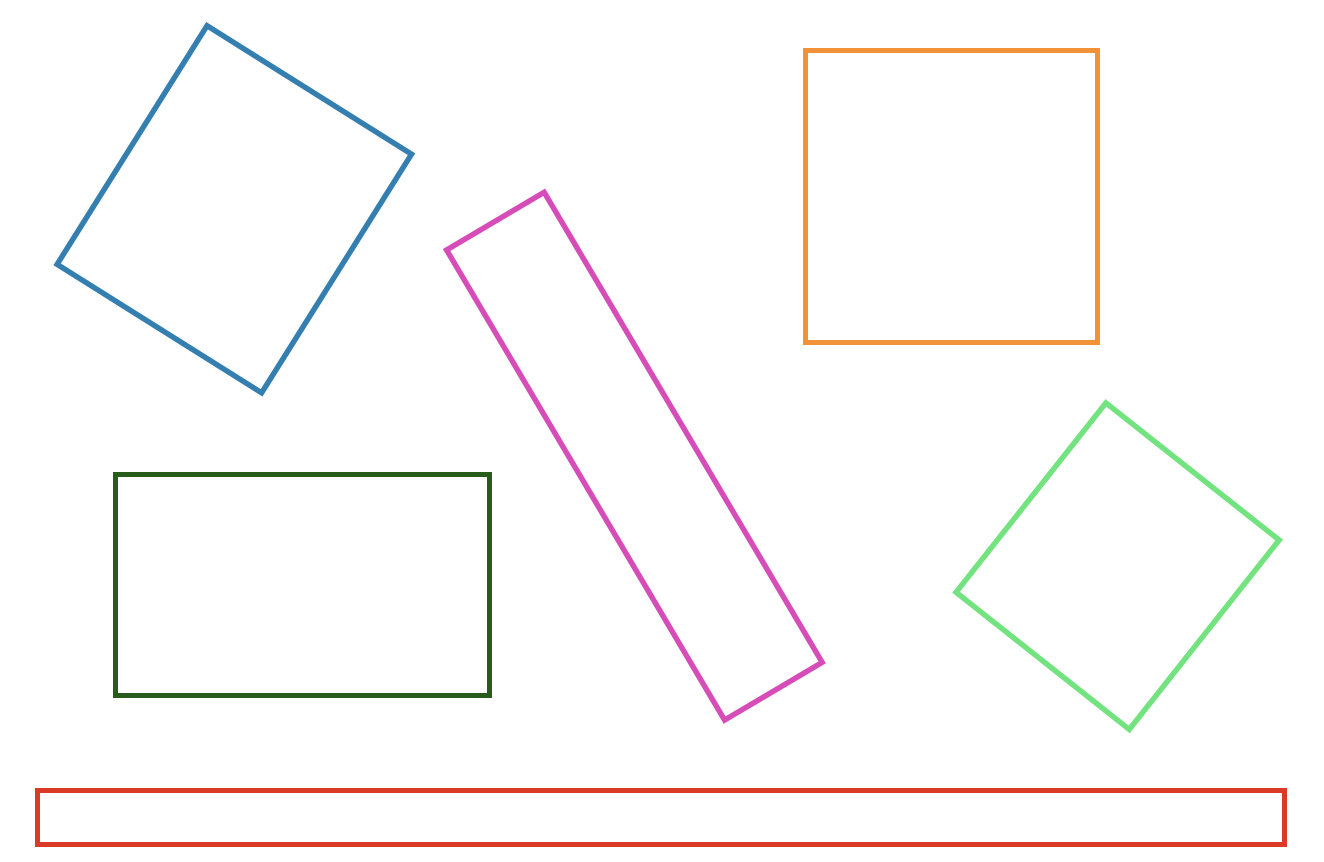
Abb. 6.3: Variationsprinzip beim Begriff Rechteck
Um dieses Prinzip für einen Begriff zu realisieren, muss man sich als Lehrkraft also Gedanken über die mathematisch relevanten und irrelevanten Eigenschaften machen. Auch eine explizite Diskussion mit den Schülerinnen und Schüler, warum diese Eigenschaften variiert werden durften (und andere nicht), kann hilfreich für das Begriffsverständnis sein.
6.2.2.2 Kontrastprinzip
Gegenbeispiele dürfen nicht für Beispiele gehalten werden, es darf nicht zu einer Übergeneralisierung kommen. Im Alltag als Beispiele empfundene Gegenbeispiele (sogenannte Fastbeispiele) müssen diskutiert werden. Relevante Merkmale müssen mindestens einmal fehlen.
Für den Rechteckbegriff relevant sind etwa die rechten Winkel (was bei Beibehaltung der gleich langen, parallelen Seiten zu einem Parallelogramm führt). Auch die Ecken-Eigenschaften und die Tatsache, dass es sich um eine Figur (und nicht um einen Körper) handelt, sind relevant (siehe Abbildung 6.4).

Abb. 6.4: Kontrastprinzip beim Begriff Rechteck
6.2.2.3 Darbietung von Beispielen und Gegenbeispielen
Zech (1998, S. 261) fasst zusammen: »Beispiele und Gegenbeispiele sind dann am effektivsten, wenn sich die Beispiele möglichst stark in den irrelevanten Merkmalen unterscheiden und die Gegenbeispiele in möglichst wenigen relevanten Merkmalen unterscheiden.«
Eine simultane Darbietung zweier stark kontrastierender Beispiele (Abbildung 6.5) oder eines Beispiels mit einem sehr ähnlichen Gegenbeispiel (Abbildung 6.6) kann weiterhin den Fokus auf die relevanten Merkmale des Begriffs lenken.

Abb. 6.5: Simultane Darbietung zweier Beispiele zum Begriff Quadrat

Abb. 6.6: Simultane Darbietung von Beispiel und Gegenbeispiel zum Begriff Achsensymmetrie
6.2.3 Begriffsfestlegung
Nach Abbildung 6.1 ist neben der Präsentation und Diskussion geeigneter Beispiele und Gegenbeispiele die Festlegung und Benennung des zu vermittelnden Begriffs von Bedeutung. Hierfür gibt es wieder vielfältige Möglichkeiten:
Spezifizieren aus Oberbegriff
Der Begriff wird als eine Besonderheit eines bereits bekannten Begriffs festgelegt, z. B. ein Parallelogramm (neuer Begriff) als ein Viereck (bekannter Oberbegriff) mit zwei Paar zueinander paralleler Seiten.
Sammeln unter neuem Oberbegriff
Dies entspricht dem umgekehrten Vorgehen: Bereits bekannte Begriffe werden unter einem Oberbegriff zusammengeführt, so können z. B. die Rationalen und Irrationalen Zahlen unter dem neuen Begriff der Reellen Zahlen gesammelt werden.
Erklären durch Konstruktionsvorschrift
Der (in der Regel) geometrische Begriff wird über seine Konstruktionsvorschrift erklärt, z. B. eine zentrische Streckung eine Figur, die entsteht, indem von einem Streckungszentrum aus Strahlen entlang der Eckpunkte einer Figur gezeichnet werden und anschließend diese Punkte mit einem festen Verhältnis entlang der Strahlen abgetragen werden.
genetische Definition
Diese Art der Begriffseinführung ähnelt der Konstruktionsvorschrift, kann sich aber auch auf eine gedankliche Entstehung eines Begriffs beziehen. So entsteht beispielsweise ein Kreis, indem von einem Mittelpunkt aus alle Punkte einer Ebene mit festem Abstand markiert werden.
rekursive Definition
Bei dieser Art von Definition wird der neue Begriff selbst genutzt, um ihn besser zu erklären. Dies kann hilfreich sein, um schwer zugängliche Begriffe zu definieren, z. B. den Begriff Term: Zahlen und Variablen sind Terme. Verknüpfungen von Termen über die Grundrechenoperationen (und daraus abgeleitete Verknüpfungen) sind wieder Terme.
Umschreibung
Nicht immer ist eine fachlich bzw. formal korrekte Definition im Schulunterricht möglich oder sinnvoll. Dann kann auf eine Umschreibung zurückgegriffen werden, z. B. der Begriff der Menge als Zusammenfassung mehrerer Elemente.
Bestandteil der Festlegung ist in der Regel auch eine konkret formulierte und meist auch notierte Definition des Begriffs. Dabei können verschiedene Anforderungen an eine Definition gestellt werden.
- Neben der fachlichen Korrektheit (die natürlich immer gegeben sein muss) ist eine möglichst einfach verständliche Formulierung von hoher Relevanz. Das heißt zum Beispiel, dass der typische mathematisch Konjunktiv (Es sei …) im Schulunterricht vermieden werden sollte.
- Weiterhin können wesentliche Eigenschaften wichtiger als die mathematische Vollständigkeit sein, sofern dies nicht zu exlatanten fachlichen Fehlern führt. Wenn beispielsweise der Kreis als Menge aller Punkte, die von einem Mittelpunkt denselben Abstand haben definiert wird, fehlt hier der Vollständigkeit halber der Zusatz, dass diese Punkte in einer Ebene liegen müssen (weil es sich sonst auch um eine Kugel handeln kann). Je nach Lerngruppe müssten Sie hier als Lehrkraft überlegen, ob diese Eigenschaft Bestandteil der Definition sein sollte oder nicht.
- Die Definition sollte an Vorwissen anknüpfen und mehrere Darstellungsebenen aufgreifen und miteinander vernetzen.
Eine in dem Sinne gelungene Definiton zeigt Abbildung 6.7. So werden die enaktive (Bastelanleitung), ikonische (Darstellung der Geraden) und symbolische Ebene (Schreibweise) miteinander verknüpft.
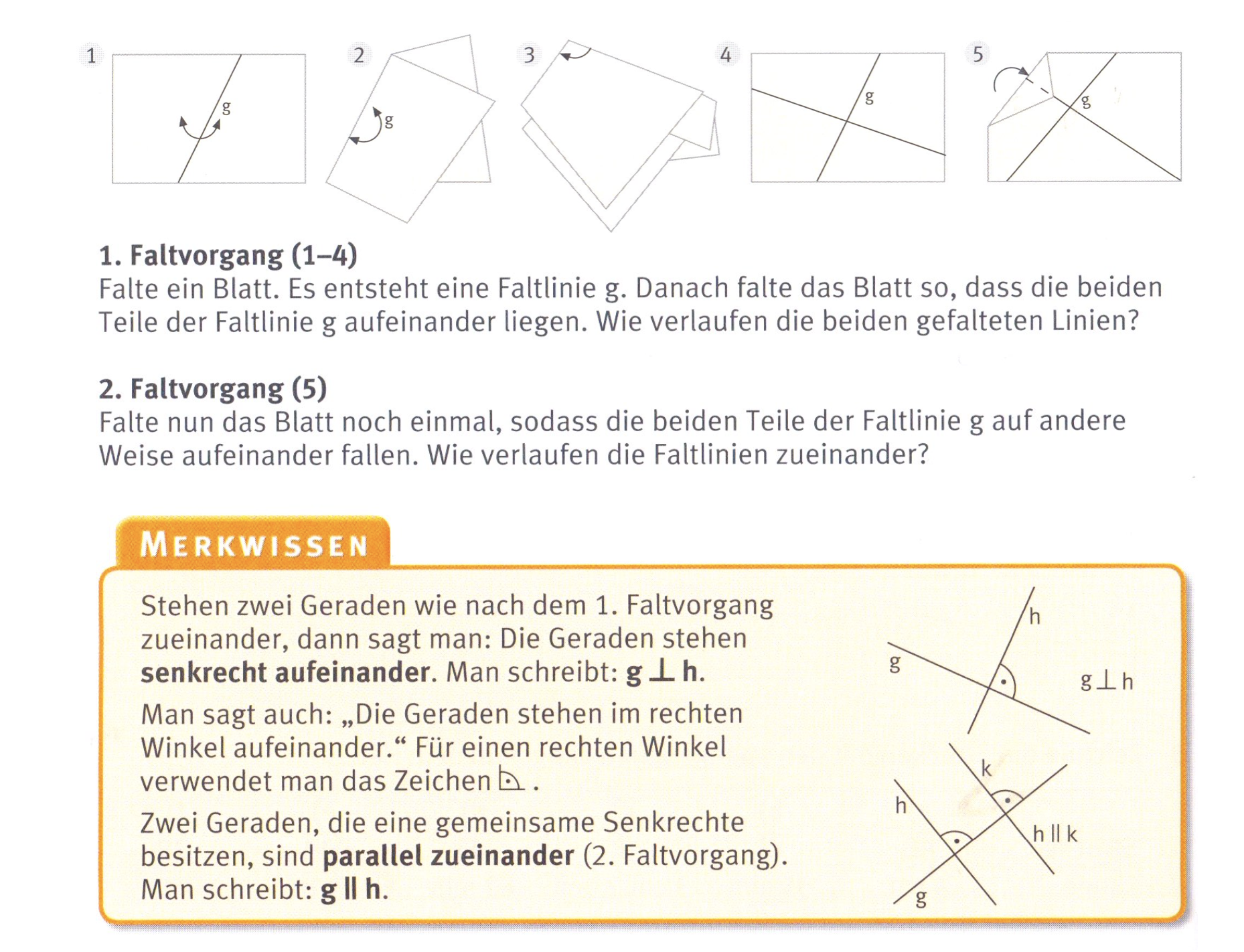
Abb. 6.7: Definition zu den Begriffen senkrecht zueinander und parallel zueinenader (Kleine, 2011, S. 78)
6.3 Zum Nachbereiten
- Lesen Sie das Kapitel zur Begriffsbildung von Weigand (2015).
- Wählen Sie einen Begriff und sammeln Sie geeignete Beispiele und Gegenbeispiele nach dem Variations- und Kontrastprinzip.
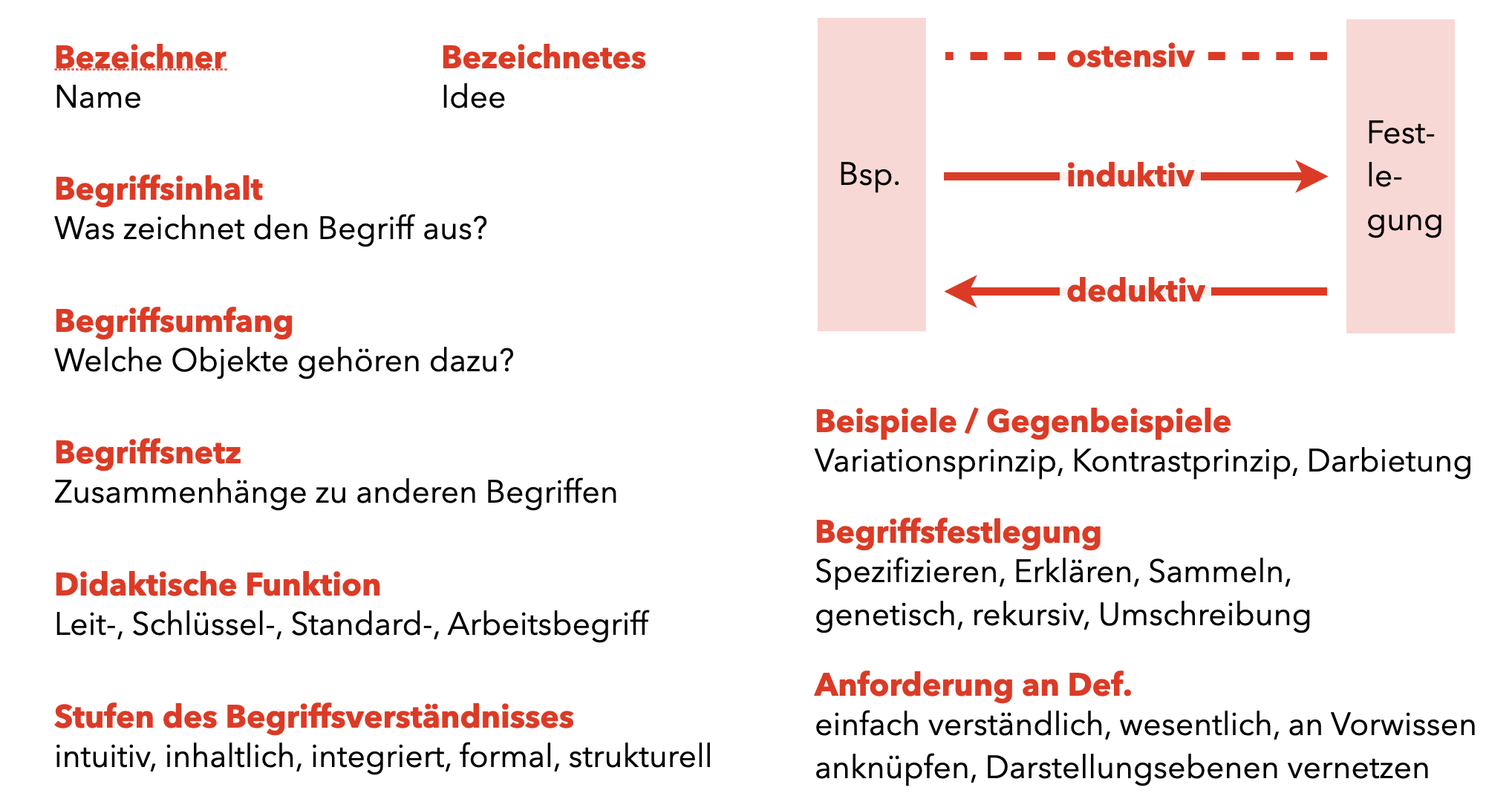
Abb. 6.8: Zusammenfassung zur Begriffsbildung
6.4 Bonus: Operative Genese
Eine weitere Möglichkeit der Begriffseinführung ist die Umwelterschließung im Geometrieunterricht durch operative Begriffsbildung nach Bender (1978). Dabei geht man davon aus, dass sich die Begriffe der Mathematik an Phänomenen aus der Umwelt orientieren.
Orientierung heißt, dass reale Objekte dahingehend analysiert werden, welchen Zweck sie erfüllen. Betrachtet man zum Beispiel Ziegelsteine, erfüllen diese den Zweck, eine Mauer bauen zu können. Um dies zu ermöglichen, müssen die Steine eine bestimmte Funktion erfüllen, im konkreten Fall das Übereinanderstapeln handlicher Objekte zu einem i. d. R. rechtwinkligen Gesamtobjekt im Raum. Aus diesen Funktionen heraus kann nun das Objekt idealisiert werden, woraus sich Bedingungen ergeben, die es erfüllen muss. Der Ziegelstein muss also aus »ebenen, paarweise parallelen Seitenflächen und rechten Kantenwinkeln« bestehen (Bender, 1978, S. 36), was zum Begriff des Quaders führt. Daraus abgeleitet kann nun wieder das Realisat hergestellt werden, also echte Quader.
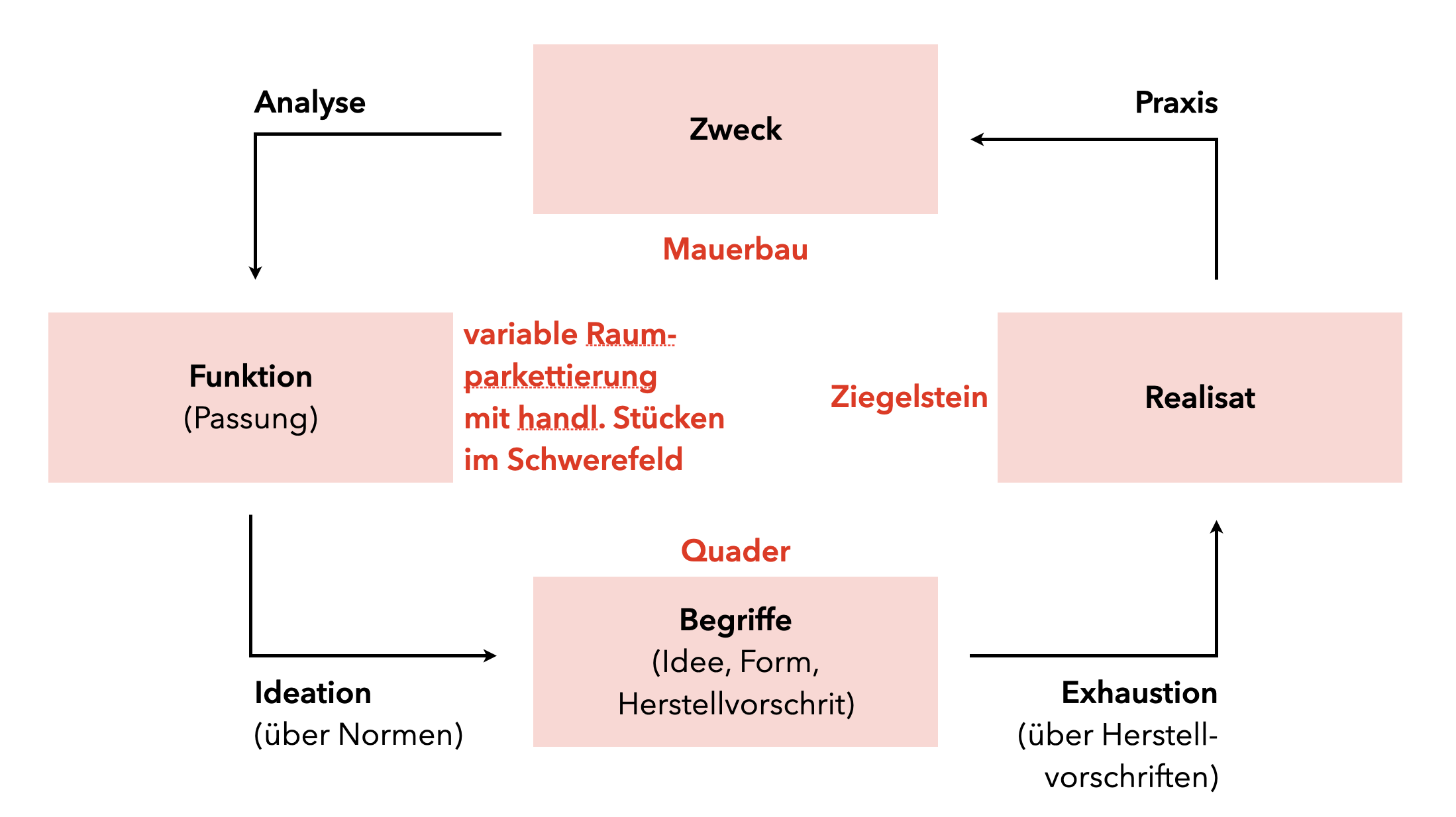
Abb. 6.9: Operative Genese in der Geometrie nach Bender (1978, S. 35)
In dem Beispiel heißt die Orientierung an der Umwelt nicht, dass Quader das Ergebnis eines Abstraktionsprozesses sind (in dem Sinne, dass man echte Ziegelsteine nimmt, ansieht und feststellt, dass sie bestimmte Eigenschaften haben), sondern genau andersrum: Echte Quader sind die Ergebnisse, denen die mathematische Idee schon (über ihre Anwendung in der Umwelt) zugrunde liegt. Ggf. ist auch ein mehrmaliges Durchlaufen des Schemas notwendig, wobei der Bau von Modellen als Zwischenschritt zwischen Idee und Realisat dienen kann.
References
Diese Repräsentanten eines Begriffs sind nicht mit dessen Repräsentationen im Sinne der Grundvorstellungsidee zu verwechseln! Die Repräsentanten sind konkrete (reale oder ideelle) Objekte, Repräsentationen dagegen Darstellungen, die ein operatives Arbeiten ermöglichen. Beides kann aber natürlich sehr ähnlich aussehen oder sogar zusammenfallen.↩︎