3 Fundamentale Ideen
Lernziele
- Sie können Fundamentale Ideen über ihre Kriterien definieren.
- Sie kennen Beispiele für Fundamentale Ideen, auch über die in den Bildungsstandards beschriebenen Kompetenzen hinaus.
- Sie können bei einzelnen Unterrichtsinhalten den Zusammenhang zu zugehörigen Fundamentalen Ideen herstellen.
Material
3.1 Begriffsklärung
Die Entwicklung Fundamentaler Ideen beruft sich auf Bruners Annahme, dass »jedes Kind […] auf jeder Entwicklungsstufe jeder Lehrgegenstand in einer intellektuell ehrlichen Form erfolgreich gelehrt werden« kann (vgl. Bruner, 1976, S. 77). Voraussetzung dafür ist, dass die Struktur eines Inhaltsbereichs in einer Art und Weise präsentiert wird, dass sie dem Kind zugänglich wird. Diese hinter den Dingen liegende Struktur hebt sich vom konkreten Inhaltsbereichen ab, ist allgemeinerer Natur und kann daher über Fundamentale Ideen beschrieben werden.
Ziel der Orientierung des Unterrichtens an Fundamentalen Ideen besteht v. a. darin, die (oftmals) isolierten Stoffelementen einzuordnen und in einem größeren Ganzen zu sehen. Im Umkehrschluss heißt dies aber auch, dass die Auswahl des konkreten Stoffes daran orientiert sein muss, wie dieser dazu beitragen kann, den dahinter liegenden mathematischen Kern und die zugehörigen Fundamentalen Ideen zu vertreten.
Die dazu seit den 1960er Jahren in Gang gesetzte Forschung führte zu vielfältigen Vorschlägen Fundamentaler Ideen der Mathematik – jedoch bisher nicht zu einem allgemeingültigen Katalog. Dieser Vielfalt in den Formulierungen und Kategorisierungen kann begegnet werden, indem Fundamentale Ideen über Eigenschaften charakterisiert werden. Im Rahmen dieser Veranstaltung wird folgende Definition genutzt, zitiert aus Schwill (1994).
Definition 3.1 (Fundamentale Idee) Eine Fundamentale Idee bzgl. eines Gegenstandsbereichs (Wissenschaft, Teilgebiet) ist ein Denk-, Handlungs-, Beschreibungs- oder Erklärungsschema, das
- in verschiedenen Gebieten des Bereichs vielfältig anwendbar oder erkennbar ist (Horizontalkriterium),
- auf jedem intellektuellen Niveau aufgezeigt und vermittelt werden kann (Vertikalkriterium),
- in der historischen Entwicklung des Bereichs deutlich wahrnehmbar ist und längerfristig relevant bleibt (Zeitkriterium),
- einen Bezug zu Sprache und Denken des Alltags und der Lebenswelt besitzt (Sinnkriterium).
Überblick zur historischen Entwicklung Fundamentaler Ideen
- von der Bank (2016, S. 37 ff.): Fundamentale Ideen der Mathematik: Weiterentwicklung einer Theorie zu deren unterrichtspraktischer Nutzung
3.2 Auswahl fundamentaler Ideen
3.2.1 Kategorisierung
Das Fehlen eines allgemeingültigen Katalogs sollte nicht davon abhalten, bestehende Auflistungen und Strukturierungen Fundamentaler Ideen zu betrachten. Angelehnt an von der Bank (2013, S. 103) und Lambert (2012), die unterschiedliche Kategorisierungen analysiert haben, sollen an dieser Stelle drei grobe Bereiche festgehalten werden.
3.2.1.1 Inhaltsideen
Inhaltsideen beziehen sich auf konkrete Inhaltsbereiche der Mathematik, die die Kriterien Fundamentaler Ideen erfüllen können. Nicht ganz zufällig spiegeln diese sich in den Leitideen der Bildungsstandards wider (Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, 2012, 2004).
Beispiele:
- Zahl
- Algorithmus
- Maß
- Raum und Form
- Funktion
- Zufall
3.2.1.2 Schnittstellenideen
Schnittstellenideen haben die Eigenschaft, dass durch sie die »Mathe(matik) wirkt« und »auch für andere Fächer in ihrer je spezifischen Weise relevant sind« (Lambert, 2012). Damit korrelieren sie mit den prozessbezogenen Kompetenzen der Bildungsstandards.
Beispiele:
- Kommunizieren
- Modellieren
- Argumentieren
- Problemlösen
- Darstellen
- Fragen
3.2.1.3 Tätigkeitsideen
Tätigkeitsideen beziehen sich insbesondere auf innermathematische Tätigkeiten, die sich über verschiedene Inhaltsbereiche hinweg zeigen. Lambert (2012) betont, dass es diese (über die Bildungsstandards hinaus) ebenfalls zu beachten gilt, wenn man einen reichhaltigen Mathematikunterricht bewirken möchte.
Beispiele:
- Approximierung
- Optimierung
- Linearität/Linearisierung
- Symmetrie
- Invarianz
- Rekursion
- Vernetzung
- Ordnen
- Strukturierung
- Formalisierung
- Exaktifizierung
- Verallgemeinern
- Idealisieren
Im Rahmen des Projektmoduls Erweitertes Fachwissen für den schulischen Kontext in Mathematik2 werden Sie insbesondere Bezüge zwischen Schul- und Hochschulmathematik auf Basis Fundamentaler Ideen herstellen, wofür die Inhalts- und Tätigkeitsideen von hoher Relevanz sind.
Diskussion Fundamentaler Ideen in den Stoffgebieten der Sekundarstufe II
- Analysis: Tietze et al. (2000a)
- Lineare Algebra/Analytische Geometrie: Tietze et al. (2000b)
- Stochastik: Tietze et al. (2002)
3.2.2 Beispiel Linearität
3.2.2.1 Horizontal- und Vertikalkriterium
Linearität ist ein wesentliches Konzept über die gesamte Schullaufbahn hinweg (und darüber hinaus). Dies spiegelt sich in vielfältigen Themenbereichen wider, die sowohl die Breite (Horizontalkriterium) als auch Tiefe (Vertikalkriterium) von Linearität und (später) auch Linearisierung zeigen. Dieser Abschnitt orientiert sich an den Darstellungen von Danckwerts (1988).
- Linearität als Phänomen tritt schon im Geometrieunterricht der Grundschule mit Geraden als essentielle geometrische Objekte auf. In der euklidischen Geometrie sind Geraden neben Punkten die Basisobjekte eines axiomatischen Aufbaus.
- Das Distributivgesetz \(a\cdot (b+c) = a\cdot b + a\cdot c\), ebenfalls bereits in der Grundschule behandelt, beschreibt einen linearen Vorgang und bietet die Grundlage für die halbschriftliche Multiplikation. Über die Schulmathematik hinaus dient es z. B. als eines der Vektorraumaxione (Skalarmultiplikation).
- Das Bestimmen eines Rechteckflächeninhalts ist ein linearer Vorgang: Ein Rechteck, das doppelt so breit ist, hat (bei gleicher Höhe) einen doppelt so großen Flächeninhalt. Betrachtet man diese Eigenschaft nicht als Phänomen, sondern als Forderung an eine Flächeninhaltsformel, so kann aus den Bedingungen \(A(a_1+a_2,b) = A(a_1,b) + A(a_2,b)\) und \(A(a,b_1+b_2) = A(a,b_1)+A(a,b_2)\) sowie der Stetigkeit in \(\mathbb{R}^+\) die Formel \(A(a,b) = a\cdot b\) abgeleitet werden.
- Lineare Zuordnungen der Art \(f(x+y) = f(x)+f(y)\) werden zu Beginn der Sekundarstufe I als proportionale Zuordnungen behandelt. Dies wird fortgeführt bei linearen Funktionen der Art \(f(x) = mx+n\), in der Fachmathematik als affin-lineare Abbildungen bezeichnet.
- Lineare Gleichungen und Gleichungssysteme sind ebenfalls bedeutsamer Bestandteil des Mathematikunterrichts. Überhaupt baut die gesamte Lineare Algebra auf lineare und affin-lineare Abbildungen auf.
- Die Strahlensätze beschreiben ebenfalls ein lineares Verhalten: Geradenabschnitte in \(c\)-facher Entfernung sind \(c\) mal so lang.
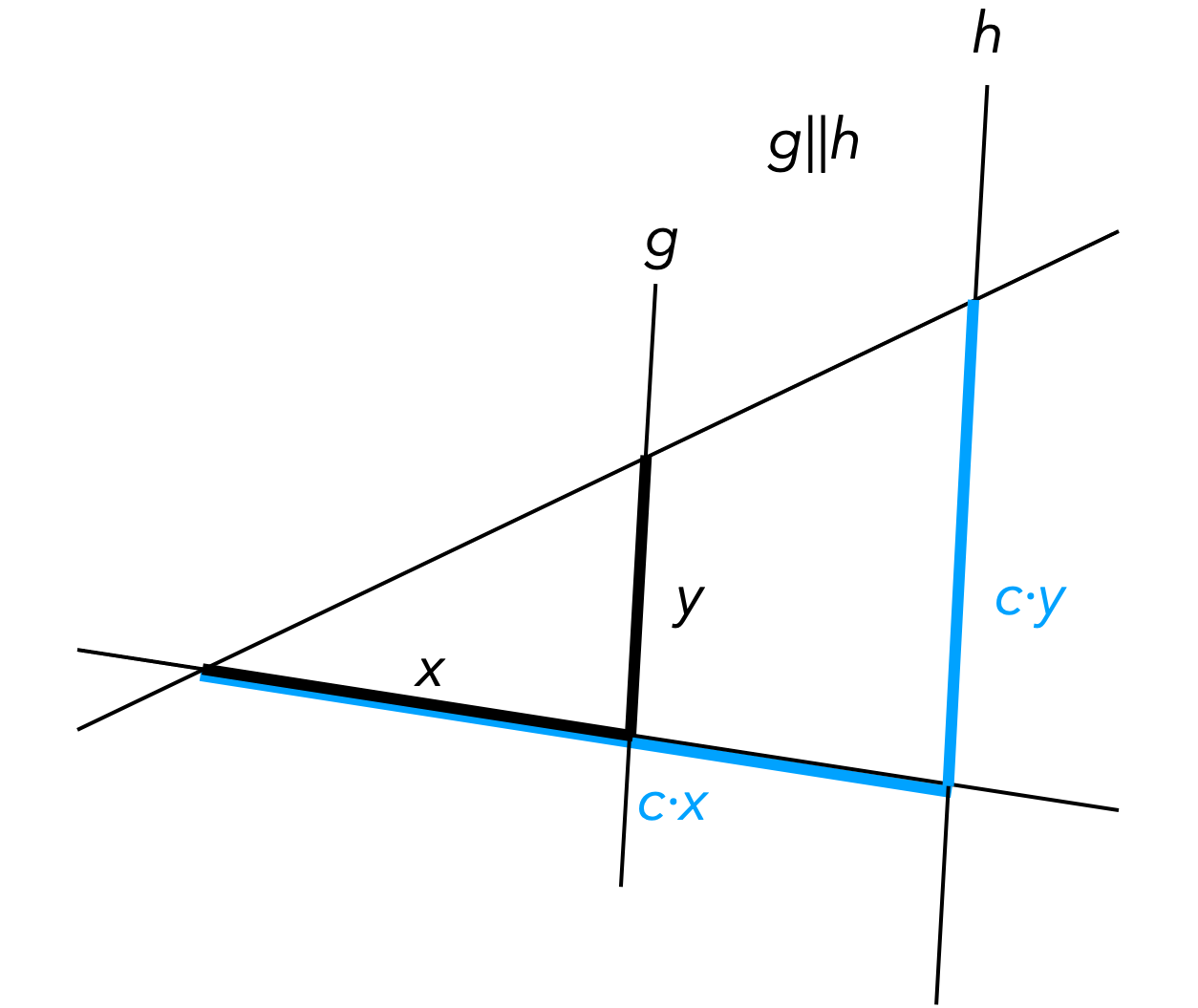
Abb. 3.1: Strahlensatzfigur
- Beim Ableitungsbegriff ist eine wesentliche Vorstellung, dass die Funktion in der Umgebung der zu betrachtenden Stelle linearisiert wird. Insbesondere bei höherdimensionalen Funktionen wird der Linearisierungsansatz weiterverfolgt. Die ebenfalls vorherrschende Tangentenvorstellung ist auf beliebige Dimensionen nicht übertragbar – der Linearisierungsansatz aufgrund seiner algebraischen Beschreibung schon.
- Eng an den Linearisierungsansatz angelehnt ist die lineare Approximation von Funktionen (z. B. \(sin(x)\approx x\) für \(x\approx 0\)). Die führt sich in der Hochschulmathematik fort, beispielsweise bei Taylor-Reihen.
- Das Bedürfnis der Linearisierung, insbesondere aus der Physik heraus, zeigt sich auch bei der Nutzung spezifisch skalierter Diagrammachsen, z. B. von Logarithmuspapier. Wegen der Äquivalenz von \(y = c\cdot a^x\) und \(\ln y = (\ln a )\cdot x + \ln c\) lassen sich beliebige Exponentialfunktionen auf Logarithmuspapier als lineare Funktionen darstellen.
- Verschiedene Näherungsverfahren, wie das Newton-Verfahren, bedienen ebenfalls sich der Linearisierung.
An dieser Stelle sei darauf hingewiesen, dass Linearität derart fundamental ist, dass selbst nicht-lineare Zusammenhänge häufig fälschlicherweise als linear angenommen werden. Dies zeigt sich zum Beispiel an den Fehlannahmen \((x+y)^2 \overset{?!}{=} x^2+y^2\), \(\sqrt{x+y} \overset{?!}{=} \sqrt{x}+\sqrt{y}\) oder \(\sin(x+y) \overset{?!}{=} \sin(x)+\sin(y)\). Derartige Fehler können Sie als Lehrkraft besser einordnen (und korrigieren), wenn Sie sich der Fundamentalen Idee Linearität (die hier eben nicht gilt) bewusst sind. Insbesondere spricht dies auch für ein Explizitmachen der Fundamentalen Idee Ihren Schülerinnen und Schülern gegenüber, so dass Sie derartigen Fehlern nicht nur mit Gegenbeispielen entgegen treten können, sondern auch eine strukturelle Einordnung sichtbar machen können.
Gerade wegen der genannten Fehlannahmen und der für die Schülerinnen und Schüler i. d. R. nicht in Zusammenhang gebrachten Dualität aus geradlinig und additiv und homogen sehen Tietze et al. (2002, S. 39) die Linearität dagegen nicht als eine im Mathematikunterricht etablierte Fundamentale Idee, »die die Schüler erkennen und die ihr Denken ordnet und anregt«.
3.2.2.2 Zeit- und Sinnkriterium
Linearität zeigt sich auch in der historischen Entwicklung der Mathematik als eine prägende Leitlinie, womit sie das Zeitkriterium Fundamentaler Ideen erfüllt. In der Linearen Algebra sei beispielsweise das Lösen linearer Gleichungssysteme im 18. Jahrhundert bis hin zum Gauß-Algorithmus im 19. Jahrhundert oder die Darstellung linearer Vorgänge mit Matrizen im 17./18. Jahrhundert erwähnt (vgl. Tietze et al., 2000b, S. 73 ff.). In der Analysis spiegelt sich die Linearität bzw. Linearisierung in der gesamten Differenzialrechnung wider, von der Interpolation nach der Jahrtausendwende über Taylors Linear perspective von 1715 (vgl. Brückler, 2018, S. 39, 119) bis in die Gegenwart der linearen Modellierung nichtlinearer Zusammenhänge.
Historische Originalausgabe
Auch Alltagssituationen bzw. die Alltagssprache ist von Linearität geprägt. Beispielsweise treten proportionale Zuordnungen unmittelbar beim Einkaufen auf, wenn Waren abgewogen und der Preis bestimmt wird. Auch reale Messvorgänge, wie z. B. die Geschwindigkeitsmessung, beziehen sich in der Regel auf die Messung von (sehr kurzen) Zeitintervallen, in denen ein lineares Verhalten angenommen wird. Das Sinnkriterium zeigt sich aber auch in Begriffen wie lineares Fernsehen oder lineare Erzählungen. Dies ist zwar keine mathematische Linearität im Sinne der Formel \(f(x+y) = f(x) +f(y)\), aber der Begriff findet in einer verwandten Bedeutung in der Alltagssprache Verwendung.
3.2.3 Gegenbeispiele
Zur Verständnisförderung sollen noch ein paar Gegenbeispiele für Fundamentale Ideen angebracht werden.
- Das bereits erwähnte Distributivgesetz an sich ist zwar elementar, aber ihm fehlt die Weite, womit es nicht das Horizontalkriterium erfüllt. Die Linearität als dahinterliegende Idee ist dagegen weit genug (vgl. ähnliche Argumentation zum Kommutativgesetz und der dahinterliegenden Idee der Invarianz bei Schubert & Schwill, 2011, S. 63).
- Der Umkehrfunktion fehlt das Sinnkriterium, da dieser Begriff in der Lebenswelt außerhab der Mathematik kaum von Relevanz ist. Dahinter liegt vielmehr die Idee der Reversibilität als »Umkehrbarkeit von Operationen mit Wiederherstellung des Ausgangszustandes« (Schubert & Schwill, 2011, S. 63).
3.3 Fund. Ideen und Stoffdidaktik
Fundamentale Ideen haben zwar ihren Ursprung in der Fachstruktur, aber sie »sind nicht Elemente der Wissenschaft an sich, sondern Produkte unseres Verstandes, die wir der Wissenschaft aufprägen. Folglich können sie nur relativ zum Menschen objektiviert werden« (Schubert & Schwill, 2011, S. 62). Hinsichtlich des Vier-Ebenen-Ansatzes liegen sie auf der semantischen Ebene mit starken Bezügen zur formalen Ebene.
Für Ihre stoffdidaktische Analyse können Fundamentale Ideen insbesondere hilfreich für die Dekonstruktion des Fachwissens und anschließende Rekonstruktion des Schulwissens sein.
Wenn sie also beispielsweise eine stoffdidaktische Analyse zur Flächeninhaltsberechnung durchführen, setzen Sie sich mit der Fundamentalen Idee des Messens auseinander. Dabei verstehen Sie Messvorgänge als Vergleiche zu einem Standardmaß (z. B. Kästchen auszählen), erkennen Zerlegungs- und Ergänzungsgleichheit als notwendige Prinzipien zur präziseren Beschreibung, sehen Dreiecke als bedeutsame Basisfiguren für Flächeninhaltsberechnungen an und haben den Blick für die Integralrechnung als verallgemeinerbare Methode zur Flächeninhaltsbestimmung krummliniger Figuren (vgl. Vohns, 2000, S. 98 ff.). Sie dekonstruieren (zerlegen) damit Ihr eigenes mathematisches Fachwissen.
Nun sind Sie in der Lage, das Wissen zur Flächeninhaltsberechnung für Schülerinnen und Schüler neu aufzubauen, also zu rekonstruieren und (unter Hinzunahme der Betrachtung von Grundvorstellungen und den restlichen Ebenen des Vier-Ebenen-Ansatzes) einen Lernpfad zu entwickeln. Im Zusammenhang mit der Integralrechnung kann dies z. B. heißen, dass Sie parallel zum Bilden von Ober- und Untersummen noch einmal eine krummlinig begrenzte Fläche durch Kästchen auszählen lassen – ggf. mit unterschiedlicher Feinheit und einer Abschätzung nach oben und nach unten. Die Fundamentalen Ideen haben für Sie damit auch eine ordnende Funktion des Unterrichtsstoffes.
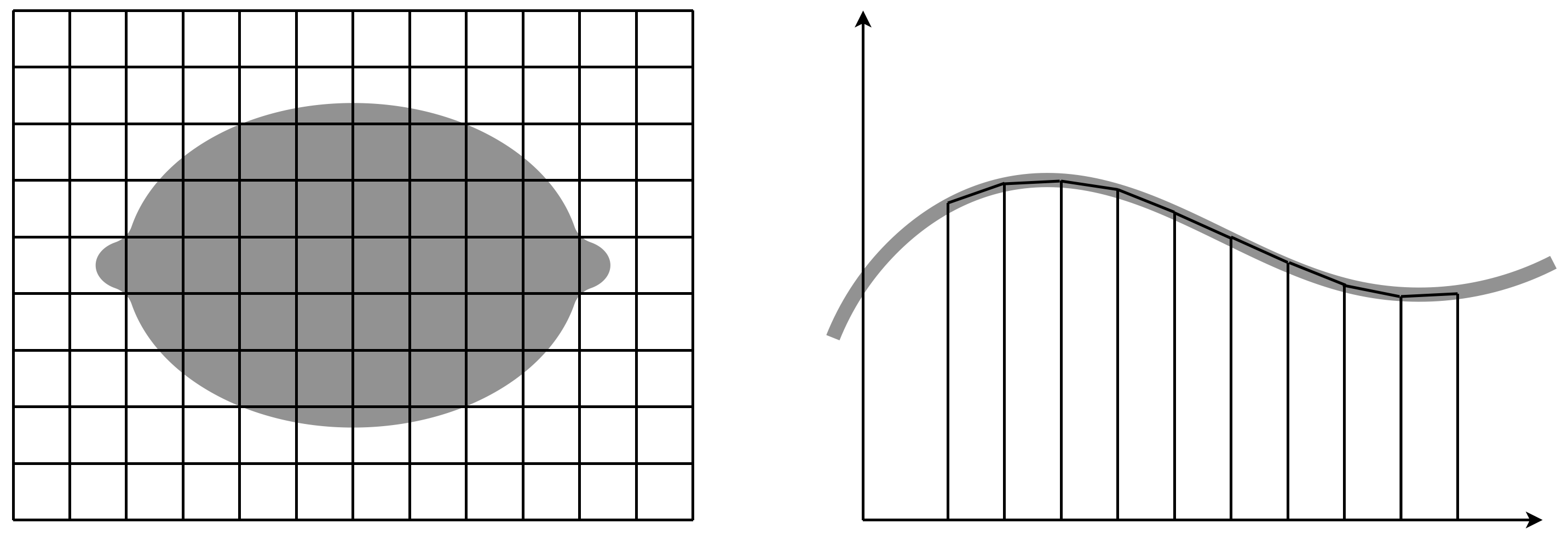
Abb. 3.2: Flächeninhaltsbestimmung
3.4 Zum Nachbereiten
- Lesen Sie das Kapitel 3.2.2 Der Begriff der Fundamentalen Ideen in der Pädagogik bei Schubert & Schwill (2011, S. 59–65).
- Wählen Sie ein Unterrichtsthema aus und stellen Sie den Bezug zu Fundamentalen Ideen her, indem Sie die zugehörigen Fragen der semantischen Ebene beantworten.