E Leitidee Daten und Zufall
Bedeutsame Lerngegenstände
- Zufallsversuch
- Wahrscheinlichkeit
- Kombinatorik
- Lage- und Streumaße
- Bedingte Wahrscheinlichkeit
- Binomialverteilung
- Normalverteilung
- Hypothesentest
Literaturempfehlungen
- Krüger et al. (2015): Didaktik der Stochastik in der Sekundarstufe I
- Tietze et al. (2002): Mathematikunterricht in der Sekundarstufe II. Band 3: Didaktik der Stochastik
E.1 Strukturierung der Leitidee
Das LISUM (o. J.-b) hat für die Primarstufe und Sekundarstufe I ein Konzeptbild herausgegeben (siehe Abbildung E.1), ergänzt durch einen didaktischen Kommentar von Kortenkamp & Kuzle (o. J.-a) und Materialien zur Diagnose und Förderung (LISUM, o. J.-a).
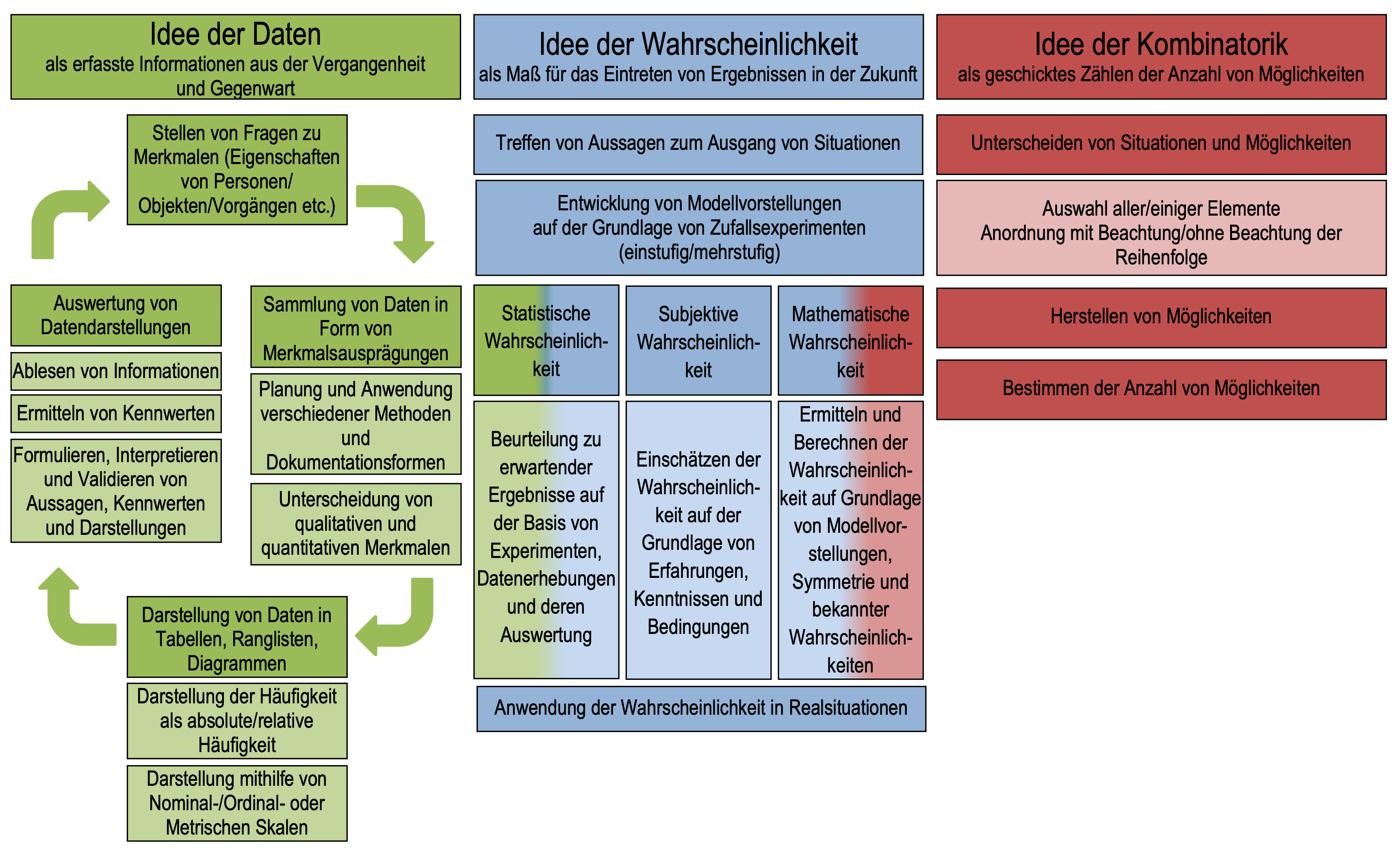
Abb. E.1: Konzeptbild zur Leitidee Daten und Zufall (LISUM, o. J.-b)
In Konzeptbild wird sichtbar, dass der Wahrscheinlichkeitsbegriff die verschiedenen Ideen miteinander in Bezug bringt, was die Bedeutsamkeit von stochastischen Vorgängen für die Leitidee hervorhebt.
E.2 Stochastische Vorgänge
Krüger et al. (2015, S. 219 f.) argumentiert, dass der häufig verbreitete Begriff des Zufallsexperiments aus fachlicher wie didaktischer Sicht ungeeignet für den Unterricht erscheint. Er begründet dies u. a. mit der Nichtnotwendigkeit des Begriffs in der Fachmathematik und damit, dass es sich nicht um ein Experiment im naturwissenschaftlichen Sinne der Hypothesenüberprüfung unter kontrollierten Bedingungen handele – die oftmals formulierte Regel der »beliebige[n] Wiederholbarkeit unter gleichen Bedingungen« sei letztlich schon ein Modell mit der Annahme der stochastischen Unabhängigkeit (Krüger et al., 2015, S. 219). Spiele, in denen der Zufall eine Rolle spielt, sind für den Mathematikunterricht höchst relevant – sollten aber nicht als Experimente aufgefasst werden. Stattdessen werden für die Grundschule der Begriff Vorgang mit mehreren möglichen Ergebnissen und für die weiterführenden Schulen der Begriff stochastischer Vorgang vorgeschlagen (Krüger et al., 2015, S. 220)
Für die tatsächliche Unterrichtsausführung ist dies insofern problematisch, da der Begriff Zufallsexperiment i. d. R. Bestandtteil der Lehrpläne ist (siehe z. B. Ministerium für Bildung, Jugend und Sport des Landes Brandenburg, 2015b, S. 59, 61) und damit unterrichtet werden muss. Sie als Lehrkraft sollten also stets die an der Verwendung des Begriffs vorgebrachte Kritik im Hinterkopf haben und dies sensibel bei Ihrer Unterrichtsgestaltung beachten. Dies kann etwa bedeuten, dass Sie dennoch eine übliche Definition des Begriffs Zufallsexperiment nutzen (siehe Abbildung E.2), aber im Unterricht die Unterschiede zu echten Experimenten thematisieren und über geeignete Beispiele und Gegenbeispiele den Begriff ausschärfen.

Abb. E.2: Schulbuchdefinition des Begriff Zufallsexperiment (Adam & Kleine, 2016, S. 18)
Grundsätzlich ist es Aufgabe der Stochastik, reale Prozesse zu modellieren, um diese mit mathematischen Mitteln greifbar (und bearbeitbar) zu machen. Dazu ist es normalerweise notwendig, die reale Situation zu vereinfachen und in ein Realmodell überzuführen (siehe Abbildung E.3. Der Begriff stochastischer Vorgang ist dann »auf der Ebene der Realmodelle angesiedelt«, mit der Verwendung des Begriffs Zufallsexperiment dagegen »verwischt man die Grenzen zwischen Realität und Modellebene« (Krüger et al., 2015, S. 219 f.).
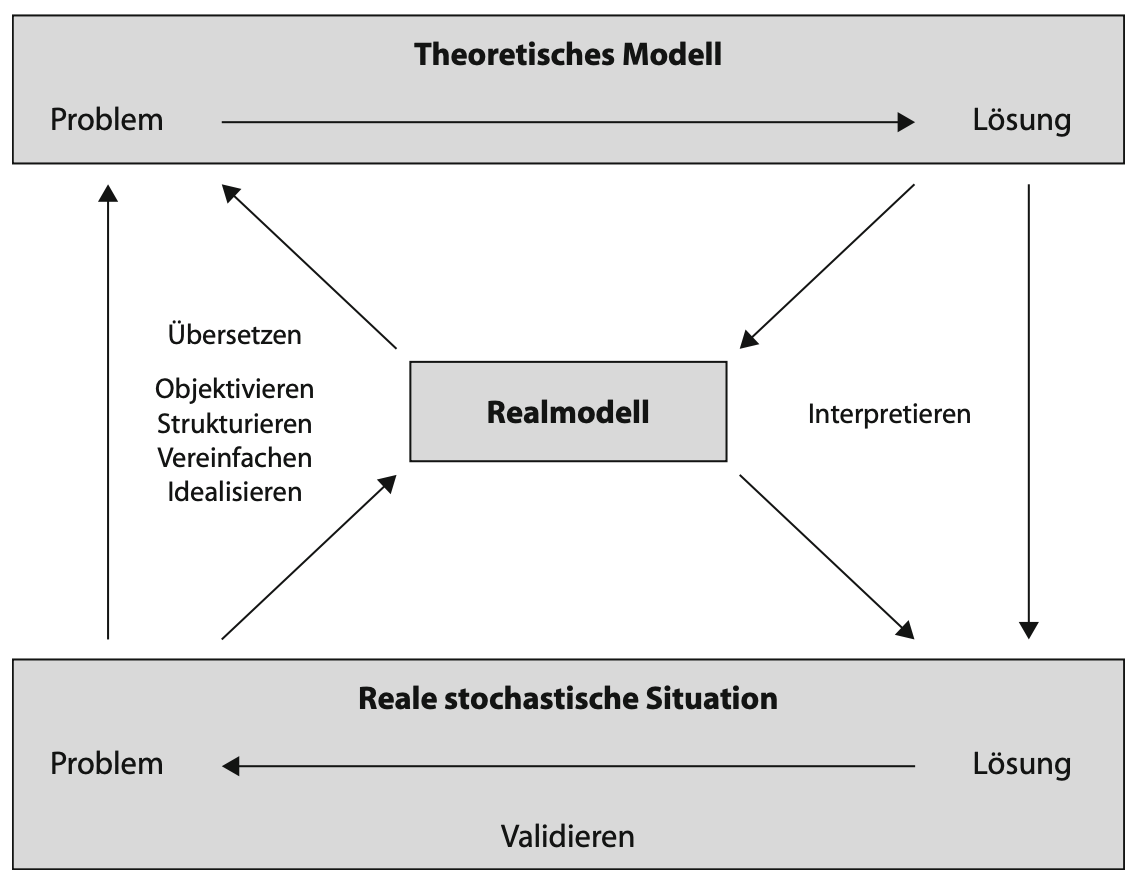
Abb. E.3: Modellierungsstruktur in der Stochastik (Krüger et al., 2015, S. 13)
Aufbauend auf diese Struktur (die »nicht als expliziter Gegenstand des Stochastikunterrichts aufzufassen« ist, Krüger et al., 2015, S. 13) können Sie Ihre Diskussionen im Unterricht leiten und Schwierigkeiten der Schülerinnen und Schüler besser einordnen, z. B.:
Wenn ein Würfel geworfen wird (reale Situation) und man die Wahrscheinlichkeit für eine Augenzahl angibt (theoretisches Modell), geht man davon aus, dass der Würfel aus sechs identischen Seiten besteht und in sich homogen ist (Realmodell). Mögliche Fragen, die auf eine solche Denkweise hinarbeiten, könnten sein: Welche Annahmen triffst du? Welche Eigenschaften muss der Würfel haben, damit du so rechnen darfst?
Wenn erstmals Zufallsgeräte (übrigens auch ein Begriff auf der Ebene der Realmodelle) genutzt werden, muss eine Untergeneralisierung vermieden werden, es sollten also frühzeitig auch nicht-Laplace-Geräte eingesetzt werden, wie Reißzwecken, Quader, sogenannte Riemer-Würfel (Riemer, 1988) oder auch Würfel-Schweine (Wikipedia, o. J.).
Wenn eine Schülerin oder ein Schüler nicht in der Lage ist, für das Ziehen einer Herz-Karte aus einem Skatblatt die Wahrscheinlichkeit anzugeben, sollten Sie als Lehrkraft herausfinden, auf welcher Ebene Schwierigkeiten bestehen. Wird die reale Situation nicht verstanden (weil z. B. die Spielkartenfarben oder der Begriff Skatblatt unbekannt sind)? Bestehen Schwierigkeiten im Aufstellen eines Realmodells (dass also das Ziehen jeder Karte mit derselben Wahrscheinlichkeit verbunden ist und dafür die Anzahl der relevanten Karten bestimmt werden muss)? Oder sind Defizite in der Theorie verortet (weil etwa nicht die Laplace-Formel für die Berechnung der Wahrscheinlichkeit angewandt werden kann oder gar Schwierigkeiten bei der Division bestehen)?
E.3 Lagemaße
Während der Vorlesungsveranstaltung wurde ein virtuelles Arbeitsmittel21 mit Cinderalla und CindyScript (vgl. Richter-Gebert & Kortenkamp, 2012) zur Erkundung von arithmetischem Mittel und Median erstellt. Abbildung E.4 zeigt einen Screenshot des virtuellen Arbeitsmittels, das auch als Cinderella-Datei zur Verfügung steht.
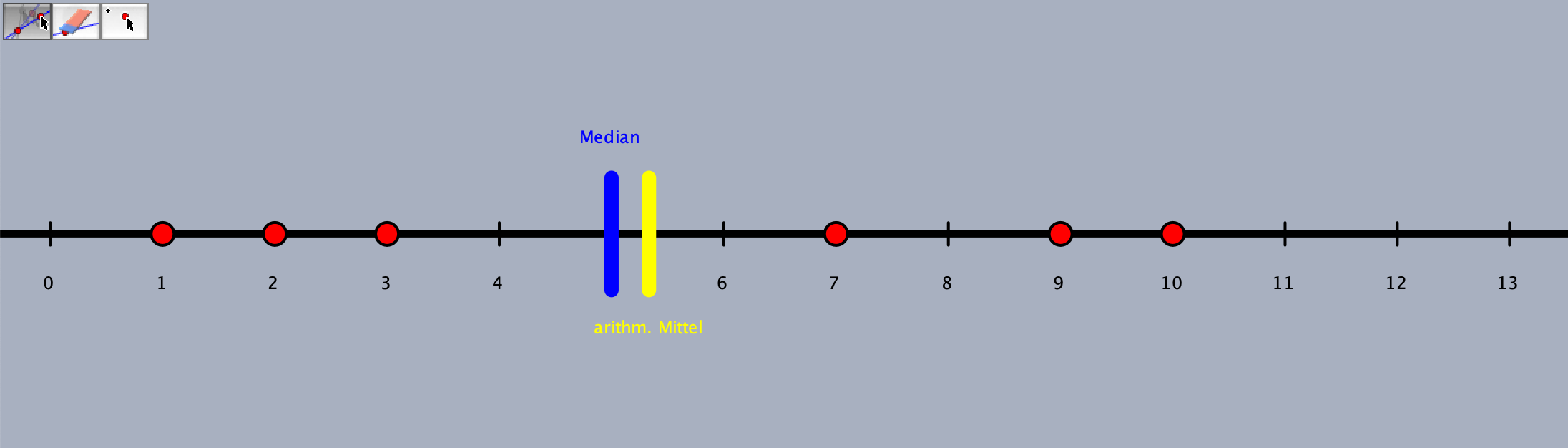
Abb. E.4: Screenshot des virtuellen Arbeitsmittels zu Lagemaßen
Anregungen für Aufgabenstellungen, die zu einer vertiefenden Beschäftigung mit den beiden Lagemaßen unter Zuhilfenahme des Arbeitsmittes führen können, sind zum Beispiel:
- Verändere die Punkte so, dass Median und arithmetisches Mittel gleich sind.
- Kannst du Punkte verschieben, so dass Median oder arithmetisches Mittel unverändert bleiben? Bei welchen Punkten geht das (nicht) und warum (nicht)?
- Wie verändert sich das beobachtete Verhalten von arithmetischem Mittel und Median bei ungerader Anzahl an Punkten?
- Zeige mit dem Arbeitsmittel, dass der Median stabil gegenüber Ausreißern ist, das arithmetische Mittel jedoch nicht.
References
zum Begriff des Arbeitsmittels siehe Kapitel zu Lernumgebungen↩︎