A Leitidee Zahl
Bedeutsame Lerngegenstände
- Zahlbereiche
- Prozente
- Kombinatorik
- Grenzwert
- Tupel, Matrizen
Literaturempfehlungen
- Padberg & Büchter (2015): Einführung Mathematik Primarstufe – Arithmetik
- Padberg & Wartha (2017): Didaktik der Bruchrechnung
A.1 Strukturierung der Leitidee
In den Bildungsstandards für die allgemeine Hochschulreife lautet diese Leitidee »Algorithmus und Zahl« (Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, 2012, S. 11), in denen für den Primarbereich »Zahlen und Operationen« (Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, 2005, S. 9).
Das LISUM (2021) hat für die Primarstufe und Sekundarstufe I ein Konzeptbild herausgegeben (siehe Abbildung A.1), ergänzt durch einen didaktischen Kommentar von Schulz (o. J.) und Materialien zur Diagnose und Förderung (LISUM, o. J.-g).
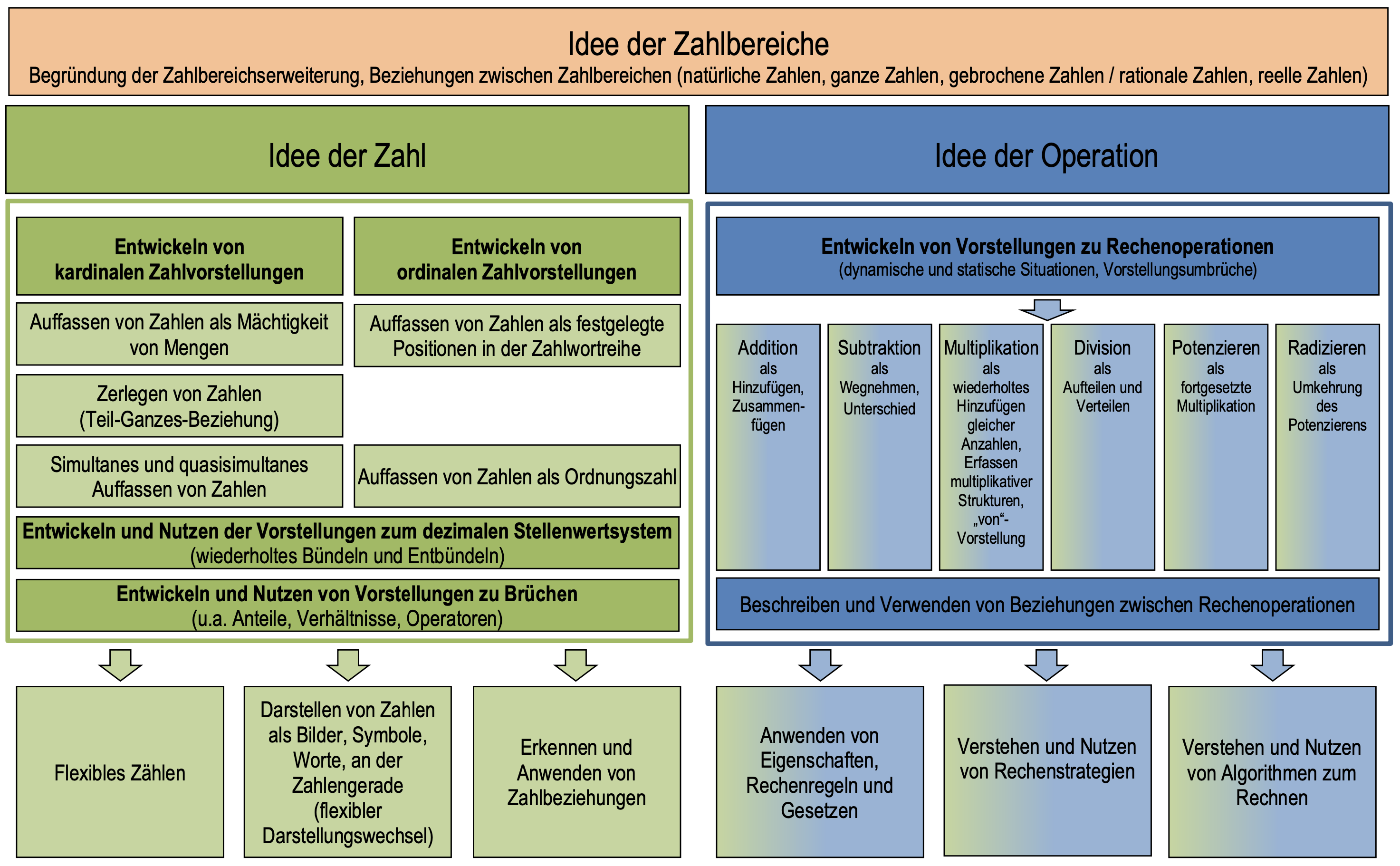
Abb. A.1: Konzeptbild zur Leitidee Zahlen und Operationen (LISUM, 2021)
A.2 Aufbau der Zahlbereiche
Die Einführung der Zahlbereiche unterscheidet sich deutlich zwischen Schule und Universität. Dies beginnt schon bei der Reihenfolge: Während in der Schule nach den Natürlichen Zahlen i. d. R. die Bruchzahlen eingeführt werden, folgt in der Hochschulmathematik normalerweise erst die Einführung der negativen Zahlen.

Abb. A.2: Zahlbereiche im Laufe der Schulzeit
Aus Abbildung A.2 wird weiterhin sichtbar, dass über einen sehr langen Zeitraum ausschließlich mit Natürlichen Zahlen gearbeitet wird, was Vorstellungen verfestigt, die dann ggf. in den weiteren Zahlbereichen nicht mehr tragfähig sind (vgl. Abschnitt 4.3.2 und die dortige Fußnote zu Fehlvorstellungen).
A.2.1 Hochschulperspektive
In universitären Veranstaltungen ist als Aufbau der Zahlbereiche üblich:
- Definition der Natürlichen Zahlen als Ordinalzahlen über die Peano-Axiome.
- Definition der Natürlichen Zahlen als Kardinalzahlen über die Anzahl der Elemente eine Menge. Dabei werden Bijektionen zwischen gleichmächtigen Mengen betrachtet und eine Zahl \(n\) kann als Äquivalenzklasse aufgefasst werden, die für alle Mengen der entsprechenden Mächtigkeit steht.
- Definition der Ganzen Zahlen, ebenfalls über Äquivalenzklassen von geordneten Paaren Natürlicher Zahlen, wobei \((n,m)\) und \((k,l)\) in Relation zueinander stehen, wenn \(n+l = k+m\) gilt. Es ist hier notwendig, über die Addition zu definieren (und nicht etwa über die Relation, wenn \(n-m = k-l\) gilt), da die Existenz eines Ergebnisses \(n-m\) ja für \(n,m\in\mathbb{N}\) noch gar nicht gesichert ist.
- Definition der Rationalen Zahlen als Äquivalenzklassen von geordneten Paaren Ganzer Zahlen, wobei \((r,s)\) und \((u,v)\) in Relation zueinander stehen, wenn \(r\cdot v = s\cdot u\) gilt. Zu Beachten ist, dass als zweiter Eintrag der Paare \(0\) ausgeschlossen wird.
- Definition der Reellen Zahlen als Äquivalenzklassen von Cauchy-Folgen, die in Relation zueinander stehen, wenn ihre Differenz eine Nullfolge ist (also sie denselben Grenzwert haben). Auch hier ist der Umweg über die Nullfolgen notwendig, da die Existenz des Grenzwertes in den Rationalen Zahlen nicht gesichert ist – es werden ja damit erst die Reellen Zahlen konstruiert.
- Definition der Komplexen Zahlen als Paare Reeller Zahlen.
Bei all den Zahlbereichserweiterungen muss stets überprüft werden, ob diese wohldefiniert sind, also die Rechengesetze im bisherigen Zahlbereich auf den neuen übertragbar sind und dies zu keinen Widersprüchen führt.
A.2.2 Schulperspektive
Auch wenn im Matheamtikunterricht keine Peano-Axiome, Äquivalenzklassen oder Cauchy-Folgen betrachtet werden, werden bei den Zahlbereichen dennoch Ideen der fachmathematischen Zusammenhänge aufgegriffen und sind für den Lernfortschritt bedeutsam.
Die kardinale Vorstellung Natürlicher Zahlen wird in der Grundschule unterstützt, indem eine bestimmte Anzahl an Objekten eingekreist werden muss und Mengen strukturiert erfasst werden (vgl. DZLM, o. J.).
Die Einführung Ganzer Zahlen über Paare Natürlicher Zahlen kann im Unterricht über sogenannte Guthaben-Schulen-Situationen besprochen werden. Dabei werden bspw. Guthaben- und Schulkarten gesammelt und untersucht, wer denselben Kontostand hat. Daran können auch einige der Rechengesetze erarbeitet werden (siehe z. B. Hattermann et al., 2014).
Die Idee der Äquivalenzklassen spielt bei Rationalen Zahlen eine Rolle, wenn besprochen wird, dass verschiedene Repräsentanten (wie z. B. \(\frac{2}{3}\) und \(\frac{4}{6}\)) für dieselbe Zahl stehen können.
Reelle Zahlen können in der Schule über Intervallschachtelungen angenähert werden, was die Idee der konvergierenden Cauchy-Folgen aufgreift. Der Fokus liegt dabei jedoch weniger in der Nichtexistenz des Grenzwertes in \(\mathbb{Q}\), sondern vielmehr in der Möglichkeit, bestimmte Zahlen (z. B. \(\sqrt{2}\)) als Rationale Zahl darzustellen.
References
Mit Fehlvorstellungen sind hier individuelle Vorstellungen der Schülerinnen und Schüler gemeint, die mathematisch nicht tragfähig und daher aus fachlicher Perspektive fehlerhaft sind. So ist etwa die Vorstellung, dass Multiplizieren vervielfacht, in den Natürlichen Zahlen tragfähig (und damit eine Grundvorstellung), in den Bruchzahlen jedoch nicht mehr tragfähig und wird dort dann zur Fehlvorstellung. Neben Fehlvorstellungen können weitere individuelle Vorstellungen Alltagsvorstellungen, Präkonzepte o. ä. sein (siehe auch Schecker et al., 2018, S. 11 f.).↩︎