7 Lehr-Lern-Prozesse
Lernziele
- Sie kennen Grundideen der Tätigkeitstheorie.
- Sie kennen die Lehrstrategie des Aufsteigens vom Abstrakten zum Konkreten und können diese mit der konkreten Ebene des Vier-Ebenen-Ansatzes und der Ausbildung von Grundvorstellungen in Bezug bringen.
- Sie sind sich der Herausforderungen im Finden von Kontexten und Kernideen bewusst.
Material
In diesem Kapitel sollen Grundideen der Tätigkeitstheorie aufgegriffen und mit der konkreten Ebene des Vier-Ebenen-Ansatzes in Bezug gebracht werden. Ziel ist es, Lernprozesse (insbesondere zur Begriffsbildung) aus theoretischer Perspektive zu beschreiben und daraus Rückschlüsse auf die Gestaltung von Unterricht abzuleiten. Die Tätigkeitstheorie ist dabei nur eine Möglichkeit, Lernen zu beschreiben – und wird hier insbesondere aufgrund des entsprechenden Forschungsschwerpunktes an der Universität Potsdam gewählt.
7.1 Tätigkeitstheoretische Sicht
7.1.1 Grundannahmen
Eine Grundannahme der Tätigkeitstheorie ist das Verständnis, dass sich Individuen aktiv-handelnd mit ihrer Umwelt auseinandersetzen, die Umwelt dabei in der Interaktion mit der Gesellschaft verändern, und beide Prozesse wiederum psychisch im Individuum abgebildet werden. Dies widerspricht bspw. der behavioristischen Annahme, dass man sich seiner Umwelt einfach nur anpasst, aber es ist auch nicht mit der konstruktivistischen Annahme zu verwechseln, nach der Individuen ein Abbild der Umwelt kognitiv rekonstruieren. Die Tätigkeitstheorie kann eher als »(moderat) konstruktivistische[r][..] Ansatz« bezeichnet werden (Giest, 2016, S. 47).
Weiterhin besteht die Annahme, dass Lernprozesse niemals direkt zwischen einem Individuum (dem Subjekt) und dem zu betrachtenden Lerngegenstand (dem Objekt) erfolgen, sondern dies stets über ein vermittelndes Werkzeug geschieht. Ein solches Werkzeug kann eine Geste sein, die Sprache (ein sogenanntes psychisches Werkzeug), Abbildungen und Skizzen, aber eben auch echte Werkzeuge wie Maschinen, Geräte und andere Hilfsmittel.

Abb. 7.1: Werkzeuge als Vermittler in der Tätigkeitstheorie
Durch die Nutzung eines geeigneten Werkzeugs ist das Subjekt damit also einerseits in der Lage, sein eigenes Wissen zu externalisieren, d. h. das Werkzeug zielgerichtet so einzusetzen, dass auf das Objekt eingewirkt werden kann. Andererseits kann das Werkzeug auch dabei helfen, Eigenschaften des Objekts zu internalisieren, indem die Werkzeugnutzung dazu führt, dass das Subjekt Wissen über das Objekt aufbaut.
Für die Gestaltung von Mathematikunterricht ist nun von besonderem Interesse, welche Werkzeuge bei bestimmten Begriffen geeignet sind bzw. wie diese auszusehen haben, um den Begriffserwerb zu unterstützen. Die Tätigkeitstheorie ist noch deutlich komplexer als hier in wenigen Zeilen dargestellt. Eine übersichtliche Einführung bietet z. B. Giest (2016), speziell für die Werkzeuggestaltung im Mathematikunterricht siehe auch Etzold (2021).
7.1.2 Gestaltung von Lehr-Lern-Prozessen
Nach einer ausführlicheren theoretischen Betrachtung schlägt Lompscher (1983a, S. 77 f.) für die Gestaltung von Lehr-Lern-Prozessen folgende Abfolge vor:
Zunächst einmal sollte den Schülerinnen und Schülern eine Anforderungssituation in ihrer Zone der nächsten Entwicklung (ZdnE) präsentiert werden. Dies ist eine Problemsituation, Aufgabe oder Fragestellung, die die Schülerinnen und Schüler zwar mithilfe ihres bisherigen Wissens und Könnens verstehen und nachvollziehen können, zu ihrer Lösung sie jedoch noch nicht in der Lage sind. Damit soll eine Motivation geschaffen werden, sich mit der Thematik tiefer auseinanderzusetzen. Es ist durchaus möglich, an dieser Stelle auch schon erste Lösungsversuche zu unternehmen. Daran ist besonders gut zu erkennen, »was wir nicht wissen bzw. können, um die Anforderung zu bewältigen« (Lompscher, 1996, S. 4).
Anschließend werden gemeinsam mit der Lehrkraft Lernziele herausgearbeitet, die den weiteren Verlauf des Lernens strukturieren sollen. Wichtig ist hier eine Unterscheidung zu Lehrzielen, die die Sicht der Lehrkraft widerspiegeln. Lernziele dagegen sind die Ziele aus Sicht der Schülerinnen und Schüler, auf die sich im individuellen Lernprozess auch bezogen werden können muss. Es bietet sich daher auch eine explizite Formulierung der Lernziele an.
Nun wird durch den Aufbau von Lernhandlungen auf den Lerngegenstand eingewirkt. Lernhandlungen sind nach Lompscher (1983b, S. 46) »relativ geschlossene und abgrenzbare, zeitlich und logisch strukturierte Abschnitte im Verlauf der Lerntätigkeit, die ein konkretes Lernziel realisieren, durch bestimmte Lernmotive angetrieben werden und entsprechend den konkreten Lernbedingungen durch den Einsatz äußerer und verinnerlichter Lernmittel in einer jeweils spezifischen Folge von Teilhandlungen vollzogen werden.« Konkreter lässt sich dies auch nicht wirklich beschreiben – je nach Lerngegenstand sind von der Lehrkraft geeignete Lernhandlungen zu identifizieren. Entscheidend ist, dass die Lernhandlungen das Wesen des Lerngegenstands repräsentieren, damit über sie das Wissen aufgebaut werden kann.
Um nun den Lerngegenstand (also das Objekt) psychisch (im Subjekt) abbilden zu können, ist eine Verinnerlichung der Lernhandlungen nötig. Nach Gal’perin bietet sich hierfür eine etappenweise Verinnerlichung an (vgl. Lompscher, 1983a, S. 66 f.):
Etappe der materiellen bzw. materialisierten Handlung
Die Handlungen werden mit dem konkreten Material bzw. Repräsentationen durchgeführt.
Etappe der sprachlichen Handlung
Die Handlungen werden nicht mehr direkt durchgeführt, aber durch äußeres (oder inneres) Sprechen beschrieben. Dabei wird i. d. R. Bezug auf die vorherigen Handlungen genommen.
Etappe der geistigen Handlung
Die Handlungen werden nun rein kognitiv durchgeführt und bedürfen weder des Materials noch der Sprache.
Darauf aufbauend ist nun das Lösen von Aufgaben möglich, die zu einer weiteren Verankerung des neu erworbenen Wissens führen sollen.
Insbesondere für die Bildung von Begriffen bietet sich für den Aufbau von Lernhandlungen und ihre Verinnerlichung das im folgenden Abschnitt beschriebene Vorgehen an:
7.1.3 Aufsteigen vom Abstrakten zum Konkreten
Die sogenannte Lehrstrategie des Aufsteigens vom Abstrakten zum Konkreten (siehe Abbildung 7.2) kann als Abwandlung einer Mischung zwischen induktivem und deduktivem Vorgehen angesehen werden.

Abb. 7.2: Aufsteigen vom Abstrakten zum Konkreten (vgl. Etzold, 2021, S. 83)
Für die Einführung eines mathematischen Begriffs wird ein konkretes Ausgangsbeispiel gewählt, an dem das Wesen des Begriffs besonders gut deutlich wird. An diesem Ausgangskonkretum werden Lernhandlungen erarbeitet, die sich zwar am Beispiel orientieren, aber verallgemeinern lassen, sodass sie dem Begriffsaufbau dienlich sind.
Im Anschluss wird, mit Unterstützung der Lehrkraft, das Wesen des Begriffs herausgearbeitet und in Form einer Ausgangsabstraktion formuliert. Dieses Vorgehen ist vergleichbar mit dem induktiven Begriffserwerb, allerdings wird nicht aus einer Vielzahl von Beispielen eine gemeinsame Eigenschaft eliminiert, sondern am charakteristischen Beispiel wird die Eigenschaft durch eine wissende Person (Lehrkraft) in Bezug auf die Handlungserfahrungen der Schülerinnen und Schüler dargestellt. Dieser Prozess wird unterstützt mithilfe von Lernmodellen – als »sinnliche Stützen geistigen Handelns« (Giest & Lompscher, 2006, S. 225). Dies können Zeichnungen, strukturierte Darstellungen, digitale Anwendungen usw. sein, die das Wesen des Begriffs beeinhalten und erlebbar machen, wie man zu diesem Wesen gelangen kann.
Der dritte Schritt, das eigentliche Aufsteigen vom Abstrakten zum Konkreten, ist nun das Abarbeiten von Konkretisierungsreihen. Hierzu werden weitere Beispiele für den Begriff betrachtet, auf die das Ausgangsabstraktum angewandt wird. Das Lernmodell dient dabei als Mittler und die Lernhandlungen werden in verallgemeinerter und ggf. auch modifizierter Form angewandt. Erst auf diese Weise ist ein echtes Durchdringen des Begriffs möglich. Dieses Vorgehen ist mit dem deduktiven Vorgehen vergleichbar, allerdings nicht im dem Sinne, dass aus einer Definition heraus die Beispiele generiert werden. Vielmehr wird auf gegebene Beispiele die Definition angewandt, ausgeschärft und damit der Begriff immer besser verstanden.
Bereits in Abschnitt 2.3.3 wurde das Beispiel des Begriffs Winkelfeld kurz dargestellt. Das Ausgangskonkretum waren dort Sichtfelder von Tieren, da an diesen die Feld-Eigenschaft eines Winkelfeldes in besonderer Weise deutlich wird und auch die weiteren Bestandteile des Winkelfeldes (Scheitelpunkt, Schenkel) eine bedeutsame reale Entsprechung (Kopf des Tieres, Begrenzung des Sichtfeldes) haben. Eine mögliche Lernhandlung war es, das Schaf so zu bewegen, dass es die gesamte Zeit über von der Kuh gerade noch so gesehen wird (siehe Abbildung 7.3).
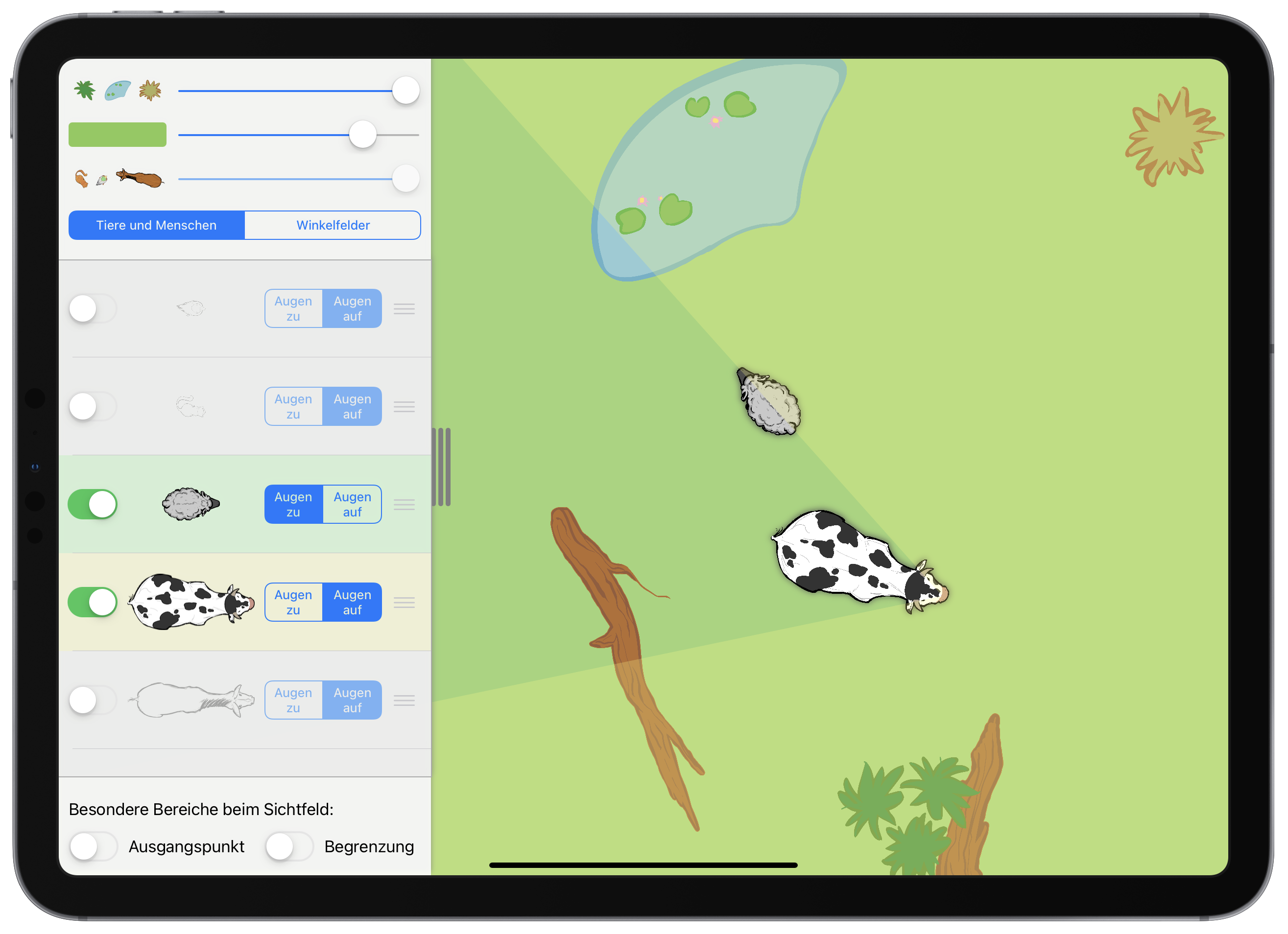
Abb. 7.3: Lernhandlung in der App Winkel-Farm (Etzold, 2019a)
Dabei erfolgt die Bewegung geradlinig, in Richtung des Kopfes der Kuh begrenzt und in die andere Richtung unbegrenzt. In verallgemeinerter Form wird damit die Strahl-Eigenschaft des Schenkels charakterisiert. Die App mit der Möglichkeit, die Bestandteile des Winkelfeldes ein- und ausblenden zu lassen sowie vom Tiermodus in den Winkelfeldmodus zu wechseln, stellt dabei das Lernmodell dar. Konkretisierungreihen sind an diesem Beispiel noch nicht erfolgt.
7.2 Bezug zum Vier-Ebenen-Ansatz
Das oben beschriebene Vorgehen bietet die Möglichkeit, die Fragen der konkreten Ebene des Vier-Ebenen-Ansatzes anzugehen. Dies wird insbesondere deutlich, wenn man den Aufbau des Schulbuchs Mathewerkstatt (Barzel et al., 2012c)10 betrachtet, das als Basis die Fragestellungen des Vier-Ebenen-Ansatzes hat. So lassen sich dort vom Vorgehen her Elemente wiederfinden, die mit den tätigkeitstheoretischen Grundlagen und der daraus abgeleiteten Gestaltung von Lehr-Lern-Prozessen vereinbar sind. Der entsprechende Zusammenhang wird auch von den Autorinnen und Autoren der Mathewerkstatt selbst implizit hergestellt, indem die im Schulbuch auftretenden Kernprozesse mit den von Bruder als Vertreterin der Tätigkeitstheorie formulierten Unterrichtssituationen in Beziehung gesetzt werden (siehe Prediger et al., 2014).
7.2.1 Kontexte, Kernideen, Kernfragen
Der von Hußmann & Prediger (2016) geforderte Kontext, der geeignet sein soll, sich dem Lerngegenstand zu nähern, kann über die Zone der nächsten Entwicklung motiviert werden und sich im Ausgangskonkretum widerspiegeln. In der Mathewerkstatt ist dies die Anküpfung auf der Einstiegsseite (am Beispiel des Ersten Intermezzos die Situation der Tiergehe, siehe Abbildung 5.1). Leuders et al. (2011, S. 4, Hervorhebungen im Original) formulieren:
»Ein sinnstiftender Kontext ist ein Ausschnitt einer inner- oder außermathematischen Welt, der folgende Anforderungen möglichst gut erfüllt:
- Er ist anschlussfähig an die Erfahrungen, Interessen und die Denk- und Handlungsmuster der Lernenden (Lebensweltbezug).
- Er ermöglicht es, authentische Fragen zu bearbeiten und dabei auch etwas über den Kontext zu lernen (Kontextauthentizität).
- Er ist problemhaltig und offen genug, um Lernende zum reichhaltigen Fragen und Erkunden anzuregen (Reichhaltigkeit).«
Daran anknüpfend werden Kernideen sichtbar gemacht, die in Form von Kernfragen formuliert und beantwortet werden (am Beispiel des Ersten Intermezzos: Wie kann ich die Größe von Flächen vergleichen?, Wie kann ich die Größe einer Fläche geschickt bestimmen?). Deren Ziel ist es, sich aus Perspektive der Schülerinnen und Schüler dem Wesen des Begriffs nähern zu können. In der Lehrstrategie des Aufsteigens vom Abstrakten zum Konkreten erfolgt dies sowohl bei der Ausübung der Lernhandlung am Ausgangskonkretum, als auch in der Verallgemeinerung der Lernhandlungen beim Entwickeln der Ausgangsabstraktion sowie in vertiefter Art und Weise beim Abarbeiten der Konkretisierungsreihen. Diese beiderseitige Entwicklung wird auch bei Leuders et al. (2011, S. 8, Hervorhebungen im Original fett oder fettkursiv, hier kursiv) sichtbar:
»Eine Kernidee umfasst in Vorschauperspektive Fragen, die die Lernenden stellen können und berücksichtigt so die subjektbezogene Dimension der Sinnstiftung. Die Kernidee in Frageform schließt an individuelle Vorerfahrungen, Zielperspektiven, Denk- und Handlungsmuster der Lernenden an und initiiert die Auseinandersetzung mit dem mathematischen Gegenstand in den Worten von Schülerinnen und Schülern[. …]
Die zu einer Kernidee gehörenden Fragen fokussieren in genetischer Perspektive konkrete zentrale Probleme, die letztlich zur Entwicklung der ›Rückschauantworten‹ der Kernidee führen.
Eine Kernidee beschreibt in der Rückschauperspektive den ideenbezogenen Kern einer längeren Lernepisode[. …]
Zur Kernidee gehört also die ›Rückschauantwort‹, in der eine allgemeine Problemstellung und die zu ihrer Bewältigung notwendigen mathematischen Konzepte benannt werden. Damit wird deutlich, dass eine Kernidee die Zwecke der Mathematisierungsprozesse und damit den Sinn der mathematischen Konzepte miterfasst.«
In der Mathewerkstatt werden über die Prozesse des Erkundens und Ordnens diese Vor- und Rückschauperspektive realisiert und in den Vertiefungen – wie es das Wort schon sagt – vertieft.
Abbildung 7.4 zeigt noch einmal die Phasen in der Mathewerkstatt (vgl. auch Prediger et al., 2014) mit einer möglichen Anknüpfung an die Lehrstrategie des Aufsteigens vom Abstrakten zum Konkreten.
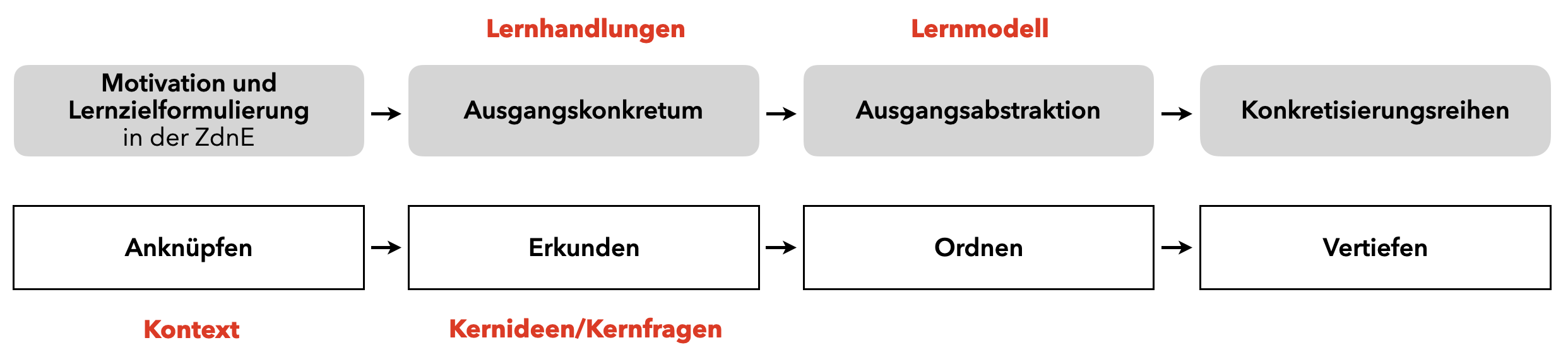
Abb. 7.4: Gegenüberstellung des Aufsteigens vom Abstrakten zum Konkreten mit dem Vorgehen in der Mathewerkstatt
7.2.2 Aufbau von Grundvorstellungen
Gemäß der Grundvorstellungsidee (siehe Def. 4.1) sollen Grundvorstellungen einen Handlungsbezug aufweisen, operationsfähige Repräsentationen beinhalten und eine Anwendung in der Realität ermöglichen.
Mit den Lernhandlungen am Ausgangskonkretumg und den Konkretisierungsreihen ist der Handlungsbezug herstellbar, außerdem kann darüber die Anwendung in der Realität sichtbar gemacht werden – sowohl beschreibend (von der Mathematik zur Realität) als auch modellierend (von der Realität zur Mathematik).
Das Lernmodell selbst kann als Repräsentation dienen, anhand dessen mit dem Begriff operiert wird. Dies ist ja auch eine Eigenschaft des Lernmodells: Sie sind eine »abstrakte Struktur des Gegenstands zusammen mit dem prinzipiellen Weg [..], der zur Aufdeckung der Struktur geführt hat« (Lompscher, 1996, S. 6).
Auch das Verinnerlichen der Lernhandlungen kann dem Aufbau von Grundvorstellungen dienen. So stellen bspw. Wartha & Schulz (2011, S. 11) ein Vier-Phasen-Modell vor, dass stark an die etappenweise Verinnerlichung von Lernhandlungen nach Gal’perin erinnert.

Abb. 7.5: Aufbau von Grundvorstellungen nach Wartha & Schulz (2011, S. 11)
Für eine ausführlichere Darstellung zu den Zusammenhängen aus der Lehrstrategie des Aufsteigens vom Abstrakten zum Konkreten und der Grundvorstellungsidee siehe auch Etzold (2021, S. 71 ff.).
7.3 Zum Nachbereiten
Lesen Sie den Beitrag von Lompscher (1996) zum Aufsteigen vom Abstrakten zum Konkreten.
Wählen Sie einen mathematischen Begriff und überlegen Sie sich, wie ein geeignetes Lernmodell für diesen Begriff aussehen kann. Sie können dabei auch spekulieren, was dieses Lernmodell können müsste (z. B. wenn es digital umgesetzt werden könnte).
References
Zur besseren Lesbarkeit wird auf die Zitation der Mathewerkstatt im restlichen Kapitel verzichtet.↩︎