9 Begriffe, Sachverhalte und Verfahren
Ziele
- Sie kennen prinzipielle Möglichkeiten, Begriffe, Sachverhalte und Verfahren einzuführen, Aneignungsprozesse mithilfe von Orientierungshilfen zu gestalten und die Inhalte zu festigen.
- Sie erkennen Gemeinsamkeiten und Unterschiede in den typischen Vorgehensweisen für Begriffe, Sachverhalte und Verfahren.
- Sie können die Prozesse tätigkeitstheoretisch einordnen.
Material
Aufbauend auf den tätigkeitstheoretischen Grundlagen soll in diesem Kapitel dargestellt werden, wie damit das Unterrichten von Begriffen, Sachverhalten und Verfahren gestaltet werden kann.
9.1 Begriffe
Sie haben in der Einführung in die Mathematikdidaktik Möglichkeiten zur Begriffsbildung kennengelernt, bei denen der Fokus insbesondere auf dem Zusammenhang zwischen geeigneten Beispielen und Gegenbeispielen zum Begriff sowie der Art der Begriffsfestlegung lag. Dieser nach Steinhöfel et al. (1988, S. 39) auch als Begriffsbildung bezeichnete Teilprozess ist jedoch noch nicht ausreichend dafür, ein Verständnis vom Begriff entwickelt zu haben – ganz im Gegenteil, er stellt nur einen ersten Schritt dar. Steinhöfel et al. (1988, S. 46) zufolge kann das Erlangen eines Begriffsverständnisses in einem idealisierten Modell in folgende Schritte eingeteilt werden:
- Bildung des Begriffs über Beispiele und Gegenbeispiele sowie der Begriffsfestlegung
- Entwicklung einer Orientierungshilfe, abhängig davon, ob die Aneignung über Identifizierungs- oder Realisierungshandlungen erfolgen soll
- Etappenweise Verinnerlichung der Aneignungshandlung
- Vertiefende Übungen zum Festigen des Begriffs.
9.1.1 Begriffe bilden
Hinweise zur Begriffsbildung finden Sie in der Vorlesung zur Einführung in die Mathematikdidaktik sowie im entsprechenden Kapitel im Skript zur Stoffdidaktik vom Wintersemester 2021/22: https://stoffdidaktik.heiko-etzold.de/2021/6-begriffsbildung.html#wege-zum-begriff
9.1.2 Begriffe aneignen
Die hier dargestellte Tabelle konkretisiert die in den Schritten 2 und 3 erwähnten Aneignungsprozesse.
| Identifizieren | Realisieren | |
|---|---|---|
| Orientierungshilfen | System der Merkmale des Begriffs; Schrittfolge zum Prüfen der Merkmale |
Handlungsvorschrift zum Herstellen oder Vervollständigen des Objekts |
| Etappe der materiellen/materialisierten Handlung | Überprüfung der Merkmale an gegebenen Objekten oder an Modellen (Zeichnungen, Diagramme); Orientierungshilfe liegt schriftlich vor | Beim Lösen entsprechender Aufgaben orientieren sich Schülerinnen und Schüler am Text der Handlungsvorschrift, die schriftlich vorliegt. |
| Etappe der sprachlichen Handlung | sprachliches Begründen des Zutreffens oder Nichtzutreffens der einzelnen Merkmale (unter zunehmender Zurückdrängung der Orientierungshilfe) | Kommentieren des Lösungsweges beim Ausführen der Handlungsschritte (Handlungsvorschrift liegt nicht mehr vor) |
| Etappe der geistigen Handlung | sofortiges Entscheiden, ob der Begriff zutrifft oder nicht (ohne Benutzung der Orientierungshilfe) | selbstständiges Lösen entsprechender Aufgaben (ohne Verwendung der Handlungsvorschrift) |
9.1.3 Begriffe festigen
Vertiefende Übungen ergeben sich v. a. durch die Einordnung des neu erlernten Begriffs in ein Begriffssystem. Hinzu kommt die Verwendung alternativer Definitionen sowie die Variablität in der Verwendung von Bezeichnungen (z. B. Variablen). Auch können Grenz- und Sonderfälle des Begriffs diskutiert werden, um ein vertieftes Verständnis zu gewinnen (vgl. Steinhöfel et al., 1988, S. 34). Eine systematische Übersicht, auch für ein ähnliches Vorgehen bei Sachverhalten und Verfahren, bietet Tabelle 9.3.
Nach Vollrath & Roth (2012, S. 48) ist ein Begriff verstanden, wenn Schülerinnen und Schüler
- die Bezeichnung des Begriffs kennen,
- Beispiele angeben und jeweils begründen können, weshalb es sich um ein Beispiel handelt,
- begründen können, weshalb etwas nicht unter den Begriff fällt,
- charakteristische Eigenschaften des Begriffs kennen,
- Oberbegriffe, Unterbegriffe und Nachbarbegriffe kennen,
- mit dem Begriff beim Argumentieren und Problemlösen arbeiten können.
Eine Vorgehensweise, die die Begriffsbildung, -aneignung und -festigung in eine unterrichtseffektive Struktur bringt, ist das Vorgehen nach dem Aufsteigen vom Abstrakten zum Konkreten, siehe Abschnitt 10.4.
9.2 Sachverhalte
Bei Sachverhalten (also Regeln, Gesetzen und Sätzen) bietet es sich an, in der Erarbeitung zwischen dem Finden des Sachverhalts, dem Finden einer Begründung und der Darstellung der Begründung zu unterscheiden.25 Im schulischen Kontext erfüllt eine Begründung i. d. R. nicht nur die Funktion, den Wahrheitsgehalt des Sachverhaltes zu sichern (diese Funktion hat ein Beweis v. a. in der Fachmathematik), sondern über die Begründung den Sachverhalt besser zu verstehen, dessen innere Struktur nachzuvollziehen und mithilfe der Begründung über den Sachverhalt zu kommunizieren. Während die ersten beiden Teilprozesse v. a. der Erarbeitung des Sachverhalts dienen, sind alle drei Teilprozesse notwendige Bestandteile für die Aneignung des Sachverhalts.
9.2.1 Sachverhalte erarbeiten
9.2.1.1 Sachverhalte finden
Für das Finden neuer Sachverhalte bestehen folgende Möglichkeiten (vgl. Vollrath & Roth, 2012, 247 f.):
Der neue Sachverhalt wird induktiv über das Entdecken von Merkmalen in gegebenen Situationen erarbeitet.
Werden bspw. Rechtecke und ihre Diagonalen gezeichnet, kann daraus entdeckt werden, dass sich die Diagonalen stets halbieren, dies also ein gültiger Sachverhalt zu sein scheint.
Der neue Sachverhalt entsteht aus dem Widerspruch zu einer angenommenen Hypothese.
Aus dem Recheckbeispiel könnte angenommen werden, dass Vierecke mit sich halbierenden Diagonalen immer Rechtecke sind. Über ein Gegenbeispiel kann aber gezeigt werden, dass dies auch bei Parallelogrammen der Fall ist. So wurde ein neuer Sachverhalt entdeckt.
Der neue Sachverhalt wird deduktiv aus bisherigen Sachverhalten gefolgert.
Der Kosinussatz kann über die Zerteilung eines allgemeinen Dreiecks in rechtwinklige Dreiecke und die mehrfache Anwendung des Satzes des Pythagoras gefolgert werden.
Nicht immer ist es sinnvoll, einen Sachverhalt zu finden. So kann etwa die Lösungsformel \(x_{1,2} = -\frac{p}{2}\pm \sqrt{\left(\frac{p}{2}\right)^2-q}\) schlecht vermutet werden, um damit die Gleichung \(0 = x^2+px+q\) zu lösen. In dem Fall wird üblicherweise mithilfe einer Herleitung direkt zur Begründung des Sachverhaltes übergegangen. Ein solches Vorgehen ist i. d. R. deduktiv.
9.2.1.2 Begründungen finden
Da das Finden von Begründungen als Problemlöseprozess aufgefasst werden kann, ist es notwendig, auf Heurismen26 Bezug zu nehmen, um Begründungen für Sachverhalte zu finden (vgl. Steinhöfel et al., 1988, 67 ff.).
- Dazu gehören heuristische Strategien, wie das Vorwärts- und Rückwärtsarbeiten, Rückführung von Unbekanntem auf Bekanntes oder Analogieschlüsse, die einzelne Beweisschritte leiten könnten.
- Heuristische Hilfsmittel wie informative Figuren können den Lösungsweg erleichtern. Gerade das Einzeichnen von Hilfslinien hat für geometrische Beweise eine hohe Bedeutung und sollte entsprechend erarbeitet werden.
- Über eine Zusammenstellung wichtiger Sachverhalte und Definitionen stehen notwendige Beweismittel zur Verfügung, vgl. auch Orientierungshilfen in Abschnitt 9.2.2.
9.2.2 Sachverhalte aneignen
Für die Aneignung eines neuen Sachverhaltes muss dieser an sich sowie seine Begründung angeeignet werden. Da beides eng miteinander zusammenhängt, sollte der Fokus daher auf der inneren Struktur des Sachverhaltes liegen. Mögliche Lernhandlungen hierfür sind:
- Prüfen der Voraussetzungen, um die Anwendbarkeit und Gültigkeit der Behauptung zu schließen. Dies erfolgt i. d. R. anhand einer (in einer Aufgabe) gegebenen Situation. Es reicht nicht aus, den Sachverhalt nur anzuwenden, sondern das Prüfen der ihm zugrundeliegenden Voraussetzungen ist ein wesentlicher Schritt in dessen Aneignung. Im Endeffekt entspricht dieses Prüfen einer Identifizierungshandlung.
- Angeben von Beispielen, auf die der Sachverhalt anwendbar ist. Dies kann auch als Realisierungshandlung aufgefasst werden.
- Herausarbeiten von Voraussetzung und Behauptung, um die Aussage des Sachverhaltes zu verinnerlichen und dessen logische Struktur zu betonen. Dies kann auch über eine sprachliche Umformulierung des Sachverhaltes (z. B. als Wenn-dann-Aussage) erfolgen.
Als Orientierungshilfen innerhalb der genannten Lernhandlungen und zur Darstellung der Begründung sind geeignet:
In strukturierten Wissensspeichern kann ein Sachverhalt oder eine Gruppe von Sachverhalten so dargestellt werden, dass dessen/deren innere Struktur hervorgehoben wird. Hierzu bietet sich eine tabellarische Übersicht an, die neben dem Namen des Sachverhaltes auch dessen Voraussetzungen und Behauptungen sowie ggf. eine verallgemeinerte (ikonische oder symbolische) Darstellung des Sachverhaltes enthält.
Tab. 9.2: Strukturierter Wissensspeicher zu Winkelsätzen, angelehnt an Steinhöfel et al. (1988, S. 69) Name des Satzes Voraussetzung Skizze Behauptung Scheitelwinkelsatz \(\alpha\) und \(\beta\) sind ein Scheitelwinkelpaar. 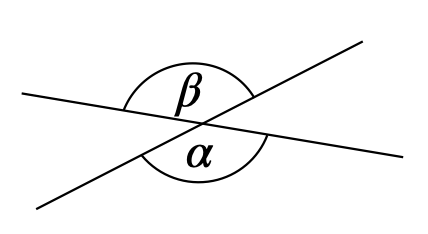
\(\alpha = \beta\) Nebenwinkelsatz \(\alpha\) und \(\beta\) sind ein Nebenwinkelpaar. 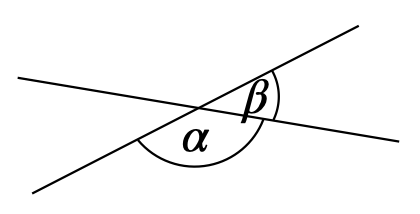
\(\alpha + \beta = 180°\) Stufenwinkelsatz \(\alpha\) und \(\beta\) sind Stufenwinkel an geschnittenen Parallelen. 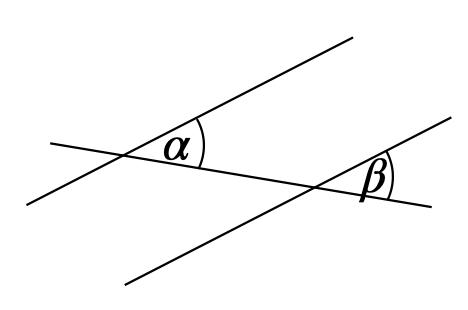
\(\alpha = \beta\) Wechselwinkelsatz \(\alpha\) und \(\beta\) sind Wechselwinkel an geschnittenen Parallelen. 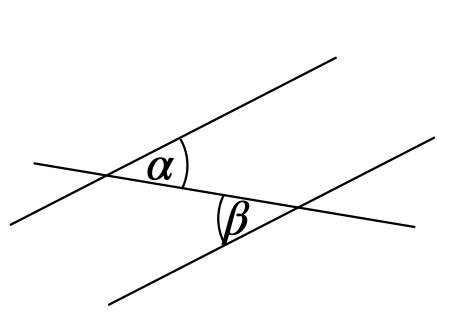
\(\alpha = \beta\) Ebenfalls der Betonung der inneren Struktur dienlich sind strukturbetonende Realisierungsmöglichkeiten. In diesen wird ein Sachverhalt dargestellt und die Darstellung dient gleichzeitig als »Ausfüllhilfe«. Solche Darstellungen mit Platzhaltern bieten sich insbesondere bei algebraischen Zusammenhängen an.
Die erste binomische Formel lässt sich in der Form \(({\large\bigcirc} + \boxed{\phantom{X}})^2 = {\large\bigcirc}^2 + 2\cdot {\large\bigcirc}\cdot \boxed{\phantom{X}} + \boxed{\phantom{X}}^2\) darstellen, wobei die Kreise und Boxen mit entsprechenden Werten oder Variablen gefüllt werden können.
Für das Finden einer Begründung kann folgende Handlungsvorschrift als Orientierungshilfe dienen (angelehnt an Steinhöfel et al., 1988, S. 72):
- Formulieren des Sachverhaltes als Wenn-dann-Aussage
- Feststellen von Voraussetzung und Behauptung
- Erstellen einer Überlegungsfigur, Bezeichnung wichtiger Teile sowie der Voraussetzung und Behauptung
- Überlegung, woraus die Behauptung folgen kann. Dabei Verwendung der Überlegungsfigur sowie Orientierung an
- Definitionen vorkommender Begriffe
- Sätzen mit gleicher Behauptung
- Sätzen mit ähnlicher Behauptung
- Abwägung, welcher Satz bzw. welche Definition geeignet ist
- Nachweis der Behauptung aus den bei 5. gewählten Beweismitteln
Für die Darstellung einer Begründung kann ein Beweisschema Orientierung bieten. So können bspw. Beweise in einer Tabelle dargestellt werden, bestehend aus einer Spalte zum Beweisschritt und einer zur zugehörigen Begründung. Dies ist insbesondere für direkte Beweise geeignet, bei denen von der Voraussetzung zur Behauptung geschlossen wird.
9.2.3 Sachverhalte festigen
Zum Festigen von Sachverhalten eignet sich nach Steinhöfel et al. (1988, S. 34) u. a. die Einschränkung einer oder mehrerer Voraussetzungen oder das Vertauschen von Voraussetzung und Behauptung, um die weitere Gültigkeit zu prüfen. Wie auch schon bei Begriffen sollten weiterhin Bezeichnungen variiert und alternative Formulierungen betrachtet werden. Auch bietet es sich an, Sachverhalte mit gleicher oder ähnlicher Behauptung zu betrachten. Auch hier sei an die systematische Übersicht in Tabelle 9.3 verwiesen.
Nach Vollrath & Roth (2012, S. 49) ist ein Sachverhalt verstanden, wenn Schülerinnen und Schüler
- den Sachverhalt angemessen formulieren können,
- Beispiele für den Sachverhalt angeben können,
- wissen, unter welchen Voraussetzungen der Sachverhalt gilt,
- den Sachverhalt begründen können,
- Konsequenzen des Sachverhalts kennen,
- Anwendungen des Sachverhalts kennen.
9.3 Verfahren
Verfahren dienen in der Mathematik der Verallgemeinerung einer Lösung von einem spezifischen Problem hin zu einer ganzen Klasse von Problemen. Für die ausführenden Schülerinnen und Schüler verschiebt sich damit der (idealerweise) kreative Prozess bei der Behandlung von Begriffen und Sachverhalten hin zu einem disziplinierten Arbeiten (vgl. Vollrath & Roth, 2012, 262 f.). Dabei darf das Verfahren jedoch nicht als geistig leeres Abarbeiten eines Lösungschemas verstanden werden, sondern auch die »Herkunft des Verfahrens« (z. B. Begründung einzelner Schritte) sind Bestandteil der Verfahrenskenntnisse.
Vollrath & Roth (2012, S. 261, Hervorhebungen im Original) zufolge beziehen sich Verfahren »in der Arithmetik in erster Linie auf die Rechenoperationen in den verschiedenen Zahlbereichen, auf das Lösen von Sachaufgaben für Größen mit Hilfe von Funktionen sowie auf die Bestimmung von Funktionswerten; in der Algebra betreffen sie das Lösen von Gleichungen, Gleichungssystemen und Ungleichungen; in der Geometrie geht es um das Konstruieren, das Berechnen von Umfängen, Flächeninhalten und Rauminhalten, das Darstellen von Körpern und in der Trigonometrie um die Dreiecksberechnungen.«
Dabei bauen Verfahren auf Begriffe und Sachverhalte auf – benötigen i. d. R. sogar mehrere von ihnen. Diese müssen also sicher zur Verfügung stehen. Oftmals ist eine Hierarchie von Begriffen und Sachverhalten bzw. vorheriger Verfahren nötig, um neue Verfahren aufzubauen (z. B. baut die schriftliche Multiplikation u. a. auf die schriftliche Addition und das kleine Einmaleins im Kopf auf, vgl. Vollrath & Roth, 2012, S. 262). Die Behandlung von Verfahren dient damit gleichzeitig auch der vertiefenden Aneignung von Begriffen und Sachverhalten.
9.3.1 Verfahren gewinnen
Entsprechend ihrer Eigenschaft, dass Verfahren dem effektiven Lösen einer Klasse von Problemen dienlich sind, können Verfahren über eine reflektierende Betrachtung der Lösung spezifischer Probleme derselben Problemklasse erarbeitet werden. Geeignete Reflexionsfragen sind dabei:
- Was haben all die betrachteten Probleme gemeinsam?
- Welche Schritte haben wir jeweils durchgeführt, um das Problem zu lösen?
- Wozu haben wir die Schritte durchgeführt?
- Warum war es möglich, die Schritte durchzuführen?
Die letzten beiden Fragen beziehen sich auf das Ziel (»Wozu?«) und den Weg (»Warum?«) der jeweiligen Verfahrensschritte.27 Vollrath & Roth (2012, S. 264) stellen am Beispiel des Lösens der Gleichung \(5x = 10\) dar, dass eine Unterscheidung zwischen Ziel (»die \(5\) auf die andere Seite bekommen«) und Weg (durch \(5\) dividieren) bei der Verfahrensgewinnung hilfreich sein kann. Während das Ziel die Notwendigkeit des Schrittes begründet, nimmt der Weg Bezüge auf die im Hintergrund wirkenden Begriffe und Sachverhalte und liefert damit eine kausale Begründung für den Verfahrensschritt.
9.3.2 Verfahren aneignen
Die Aneignung eines Verfahrens erfolgt i. d. R. über dessen Anwendung. Im Sinne der etappenweise Ausbildung bedeutet dies (Steinhöfel et al., 1988, S. 118):
- Auf der Etappe der materiellen/materialisierten Handlung liegt der Verfahrensablauf in schriftlicher Form vor.
- Auf der Etappe der sprachlichen Handlung liegt der Verfahrensablauf nicht mehr schriftlich vor. Die einzelnen Schritte werden von den Schülerinnen und Schülern während der Ausführung kommentiert.
- Auf der Etappe der geistigen Handlung führen die Schülerinnen und Schüler das Verfahren selbstständig und ohne schriftlich vorliegenden Verfahrensablauf aus.
Als Orientierungshilfe dient die schriftliche Fixierung des Verfahrensablaufs selbst – als Wortvorschrift, als Flussdiagramm bzw. als Graph o. Ä.
9.3.3 Verfahren festigen
Verfahren können u. a. gefestigt werden, indem einzelne im Verfahren auftretende Operanden spezialisiert werden (z. B. die beiden Summanden bei der schriftlichen Addition) – dies entspricht im Endeffekt einer Fallunterscheidung. Auch ist die Untersuchung unterschiedlicher Reihenfolgen der Verfahrensoperationen oder eine Variabilität der Darstellung des Verfahrens (z. B. Blockschema, Wortvorschrift, Graph, …) möglich. Weiterhin können Unter- bzw. Oberalgorithmen betrachtet, Umkehroperationen gebildet oder unterschiedliche Variablengrundbereiche untersucht werden (vgl. Steinhöfel et al., 1988, S. 34).
Nach Vollrath & Roth (2012, 49 f.) ist ein Verfahren verstanden, wenn Schülerinnen und Schüler
- wissen, was man damit erreicht,
- wissen, wie es geht,
- es auf Beispiele anwenden können,
- wissen, unter welchen Voraussetzungen es funktioniert,
- wissen, warum es funktioniert.
9.4 Zusammenfassung
In den letzten Abschnitten hat sich gezeigt, dass die Behandlung von Begriffen, Sachverhalten und Verfahren grundsätzliche Ähnlichkeiten aufweisen. So konnten stets die Teilprozesse einer Erarbeitung (Begriffe bilden, Sachverhalte und ihre Begründungen finden, Verfahren gewinnen), einer Aneignung (unter Zuhilfenahme von Orientierungshilfen mit dem Ziel der etappenweie Ausbildung geistiger Handlungen) und einer Festigung identifiziert werden. Für letztere zeigt Tabelle 9.3 noch einmal eine Gegenüberstellung von Möglichkeiten.
| Begriffe | Sachverhalte | Verfahren | |
|---|---|---|---|
| Verwendung von Spezial- und Extremfällen | Unterbegriffe; Grenzfälle |
Einschränkung einer oder mehrerer Voraussetzungen im Gültigkeitsbereich; Fallunterscheidungen |
Spezialisierung von Operanden (Fallunterscheidungen) |
| Umformulieren | verschiedene Definitionsarten;Definition in Merkmalssystem verwandeln | verschiedene logisch gleichwertige Formulierungen | evtl. unterschiedliche Reihenfolge der Operationen |
| Verwendung unterschiedlicher Bezeichnungen | Merkmale nicht an feste Variablensymbole binden | Voraussetzungen und Behauptungen nicht an feste Symbole binden | unterschiedliche Formalisierungen (Blockschema, Wortvorschrift, Graph, …) |
| Bekanntes Neuem gegenüberstellen und Zusammenhänge erkennen lassen | Oberbegriffe; Einordnung in Begriffssystem |
Sätze mit gleicher Behauptung; Sätze mit ähnlicher Behauptung |
Unteralgorithmen; Oberalgorithmen |
| Umkehrungen bilden | Voraussetzungen und Behauptungen vertauschen | Umkehroperationen bilden | |
| Bedingungen variieren | Merkmalsvariation durch Weglassen bzw. Hinzufügen von Merkmalen, Ändern der log. Verknüpfung | Weglassen bzw. Hinzufügen von Voraussetzungen | unterschiedliche Variablengrundbereiche |
Weiterführende Möglichkeiten zur Erarbeitung von Begriffen, Sachverhalten und Verfahren stellen Vollrath & Roth (2012, 227 ff.) dar.
9.5 Zum Nachbereiten
Beschreiben Sie für ein Verfahren aus der Sekundarstufe I unterrichtliche Möglichkeiten, dieses zu gewinnen.
Entwickeln Sie, entsprechend der Zusammenfassung in Tabelle 9.3, Festigungsaufgaben zum Begriff Erwartungswert, zum Sachverhalt Satz des Pythagoras oder zum Verfahren Polynomdivision.
References
Spezifischer sprechen einige Quellen auch von der Satzfindung, Beweisfindung und Beweisdarstellung, z. B. Steinhöfel et al. (1988, S. 59)↩︎
Eine Übersicht über Heurismen bietet bspw. die Webseite https://proffi-m.de/theorie.↩︎
Vollrath & Roth (2012, S. 264) verweisen hier auf die umgangssprachliche Vermischung der beiden Fragen »Wozu?« und »Warum?«.↩︎