11 Arithmetik und Algebra

Ziele

• Sie haben einen Überblick, was Arithmetik- und Algebra-Unterricht auszeichnet.
  
• Sie können den Zusammenhang zwischen den Sachgebieten Arithmetik und Algebra und den zugehörigen Leitideen beschreiben.
  
• Sie kennen Verfahren zum näherungsweisen Bestimmen von Quadratwurzeln sowie deren algorithmische Umsetzung.

Material

• Folien zum Kapitel 11 (pdf, Keynote)

Literaturempfehlungen

• Padberg & Benz (2021): Didaktik der Arithmetik: fundiert, vielseitig, praxisnah
• Weigand et al. (2022): Didaktik der Algebra: nach der Vorlage von Hans-Joachim Vollrath

In diesem und den folgenden Kapiteln sollen für die einzelnen Sachgebiete der Mathematik teils einige allgemeine Kommentare zur Didaktik des jeweiligen Sachgebiets getroffen und stets an ausgewählten Lerngegenständen mathematikdidaktische Hintergründe illustriert werden. Die Auswahl der Lerngegenstände erfolgt dabei interessen- und zufallsgesteuert und stellt keine systmatische Betrachtung dar.

11.1 Übergang Arithmetik → Algebra

»In der Arithmetik sind Zahlen die Objekte des Handelns.« Weigand et al. (2022, S. 40) formuliert diesen Satz, um im Kontrast dazu zu beschreiben, dass sich in der Algebra »der Fokus vom Handeln mit Zahlen zum Handeln mit unbekannten Größen [verändert]. Dabei können Lernende die bekannten Regeln des Operierens mit Zahlen auf die neuartige Situation übertragen, in der Zahlen unbekannt sind.« Der Mathematikunterricht der Sekundarstufe I ist geprägt durch diesen gedanklichen Übergang von der Arithmetik zur Algebra, der aber durchaus auch schon in der Grundschule beginnen kann, etwa beim halbschriftlichen Rechnen (siehe z. B. Padberg & Benz, 2021, 191 ff.). »Aus der Perspektive des Lehrens und Lernens von Algebra beginnt die Auseinandersetzung mit Algebra dort, wo Lernende allgemeine arithmetische Strukturen erkennen oder erkunden« (Weigand et al., 2022, S. 39). Die bedeutsamsten Lerngegenstände zur Algebra sind demnach Variablen, Terme und Gleichungen.

Die Algebra erhält im Schulunterricht drei wesentliche Bedeutungen (Zitate entnommen aus Weigand et al., 2022, S. 1 ff.):

• Algebra als Formelsprache. »Mithilfe von Variablen, Termen und Gleichungen kann ein Sachverhalt in der Formelsprache dargestellt werden.« Dies wird beispielsweise bei der binomischen Formel \((a+b)^2 = a^2+2ab+b^2\) sichtbar, die das Distributivgesetz für einen bestimmten Fall beschreibt.

• Algebra als Werkzeug. Demnach ist die »Algebra ein Hilfsmittel und Werkzeug, um geometrische, physikalische oder Anwendungsprobleme durch Formelsprache auszudrücken und so zu lösen«. So könn etwa die Kosten in Euro für eine Taxifahrt über die Gleichung \(K = 4,4+2,1t\) beschrieben werden, wenn \(t\) die gefahrenen Minuten darstellt.

• Algebra als Denkweise. »Algebraisches Denken zeigt sich somit im Umgang mit Denkobjekten beim Übergang von konkreten zu unbestimmten Objekten und beim Operieren auf der symbolischen Ebene.« Dies kann etwa bei der Betrachtung von Musterfolgen der Fall sein. Neben der Anzahl an Würfeln in den einzelnen Schritten in Abbildung ? könnte das Interesse darauf gelegt werden, wie sich die Anzahl von Schritt zu Schritt verändert und wie viele Würfel dann im \(n\)-ten Schritt vorhanden sind.

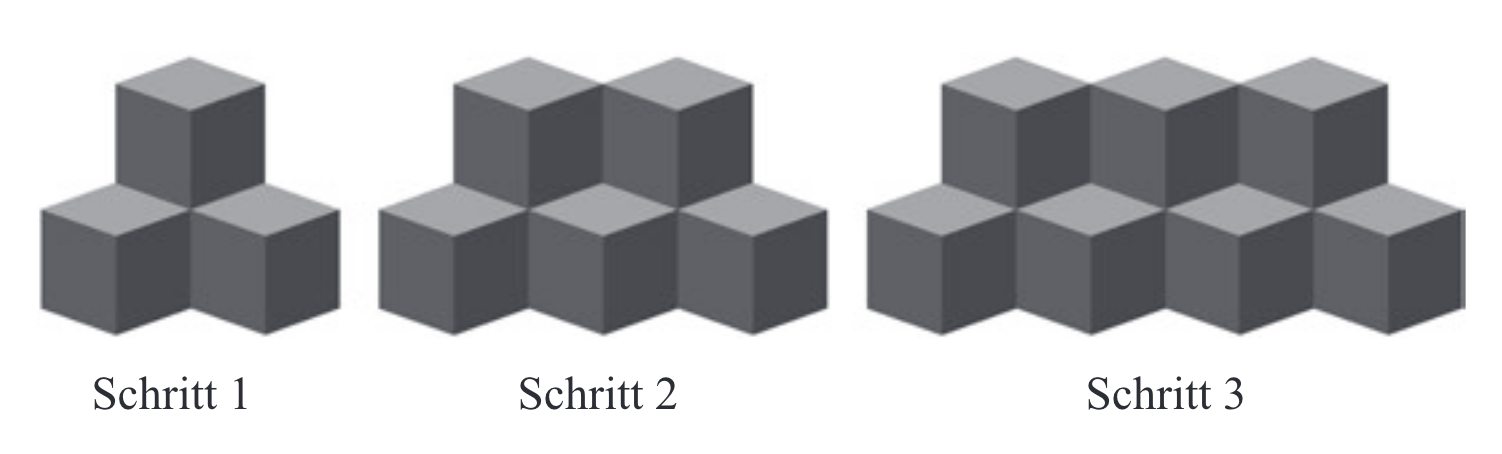
Abb. 11.1: Musterfolge zum Übergang der Arithmetik zur Algebra (Weigand et al., 2022, S. 8)

11.2 Wurzeln

11.2.1 Begriffsverständnis

In diesem Abschnitt werden Begriffsinhalt, Begriffsumfang und Begriffsnetz sowie verschiedene Stufen des Begriffsverständnisses zum Wurzelbegriff diskutiert³¹.

Zunächst ist festzuhalten, dass die Wurzel bzw. das Wurzelziehen die Umkehrung des Quadrierens im Bereich der nichtnegativen Zahlen ist. Diese Nichtnegativität ist übrigens im Unterricht besonders herauszuarbeiten. Während \((-3)^2 = 9\) und \(3^2= 9\) ist, also die Gleichung \(x^2 = 9\) zwei Lösungen in den reellen Zahlen hat, ist \(\sqrt{9} = 3\) eindeutig festgelegt. Man kann also nicht pauschal von der Wurzel als die Umkehrung des Quadrates sprechen.³² Weiterhin gehört zum Begriffsinhalt die Eigenschaft, dass Wurzeln nicht immer rational sein müssen, auch wenn die Zahl, aus der die Wurzel gezogen wird, rational ist (z. B. bei \(\sqrt{2}\)). Der Wert einer Wurzel lässt sich jedoch mittels rationaler Zahlen annähern³³. Das Vorgehen zum Finden einer Annäherung kann durchaus auch als Bestandteil des Begriffsinhalts aufgefasst werden.

Wurzeln können demnach alle nichtnegativen reellen Zahlen sein, da für jede (rationale oder reelle) Zahl \(a\geq 0\) eine reelle Zahl \(x\geq 0\) gefunden werden kann, für die \(x^2 = a\) gilt. Dieser Begriffsumfang kann sich jedoch erst schrittweise entwickeln, da mit der Einführung des Wurzelbegriffs in der Regel noch nicht die reellen Zahlen bekannt sind. Die Menge aller Wurzeln rationaler Zahlen besteht zwar aus nichtnegativen reellen Zahlen – aber noch nicht aus allen (denn z. B. \(\sqrt{\pi}\) existiert ja auch). Ein vollständiger Begriffsumfang des Wurzelbegriffs ist also erst dann ausgeprägt, wenn die reellen Zahlen eingeführt wurden.

Eng verbunden ist der Wurzelbegriff mit dem des Quadrates (sowohl algebraisch als auch geometrisch) und den reellen Zahlen (als Lückenfüller der rationalen Achse). Auch das Wurzelziehen bzw. Radizieren³⁴ als verwandte Arbeitsbegriffe gehören zum engen Begriffsnetz. Bei der Betrachtung der Gleichung \(x^2 = a\) sind auch Basis und Exponent sowie der Radikant, v. a. in der Schreibweise \(\sqrt{a} = x\), Bestandteile des Begriffsnetzes. Der Wurzelexponent wird dann v. a. bei höheren Exponenten von Bedeutung, wenn er in der Schreibweise \(\sqrt[n]{a}\) auftritt. Ob die Intervallschachtelung als Fachbegriff im Zusammenhang mit dem Wurzelziehen auftauchen muss, sollte abhängig von der Lerngruppe entschieden werden – bekommt damit aber eine besondere Bedeutung als Begriff eines Verfahrens.

Hinsichtlich des Wurzelbegriffs liegt ein intuitive Begriffsverständnis vor, wenn die Schülerinnen und Schüler Wurzeln als Seitenlängen zu Quadraten mit vorgegebenen Flächeninhalten auffassen oder dies in einer algebraischen Sichtweise nachvollziehen. Zum inhaltlichen Begriffsverständnis gehört darauf aufbauend hinzu, dass es sich stets um nichtnegative Werte handeln muss. Ein integriertes Begriffsverständnis liegt vor, wenn die Monotonie und nicht-Linearität erkannt ist, also bspw. die näherungsweise Bestimmung einer Wurzel möglich ist. Auch der begriffliche Zusammenhang zu Quadrat, Basis und Exponent kann auf dieser Stufe von den Schülerinnen und Schülern hergestellt werden. Bestandteil der Stufe ist (später) ebenfalls die Verknüpfung zu höheren Potenzen und deren \(n\)-te Wurzeln. Das formale Begriffsverständnis geht einher mit der Kenntnis und Anwendbarkeit der Definition der Wurzel, hier insbesondere auch die Fähigkeit zu begründen, warum es keine negativen Wurzeln bzw. keine Wurzeln aus negativen Zahlen gibt.

11.2.2 Wurzelbehandlung

Angelehnt an die Mathewerkstatt für die Klassenstufe 9 (Barzel et al., 2016, 92 ff.) sowie die Überlegungen in den Kapiteln 8 und 9, bietet sich folgende Behandlung des Wurzelbegriffs an:

1. Es kann prinzipiell davon ausgegangen werden, dass den Schülerinnen und Schülern Quadrate bekannt sind und sie aus diesen Seitenlängen abmessen und den Flächeninhalt berechnen können. In Hinblick auf die Zone der nächsten Entwicklung sind sie noch nicht in der Lage, aus gegebenen Flächeninhalten die Seitenlänge eines Quadrates zu berechnen bzw. halbquantitive Zusammenhänge zu erzeugen (z. B. Wie ändert sich die Seitenlänge, wenn der Flächeninhalt halbiert wird?). Jedoch können sie diese Anforderungssituation mit ihrem bisherigen Wissen verstehen.

   Der (innermathematische) Kontext ist also das Bestimmen einer Seitenlänge eines Quadrates bei gegebenem Flächeninhalt. Dies kann u. a. dadurch konkretisiert werden, dass zu einem Quadrat dasjenige mit dem halben Flächeninhalt gesucht wird. Dies erhöht die Konxtauthentizität dahingehend, das es sich um ein historisch relevantes Problem handelt (vgl. Barzel et al., 2016, S. 94). Dabei ist es reichthaltig genug, auch von der Halbierung abzusehen und allgemeinere Zusammenhänge zu erkunden. Ein erster Lösungsversuch ist zum Beispiel über das Falten eines quadratischen Blatt Papiers möglich (indem alle vier Ecken auf den Mittelpunkt gefaltet werden). Durch einen Vergleich des ursprünglichen und des gefalteten Quadrates kann man erkennen, dass die Seitenlänge nicht einfach halbiert werden kann.

2. Als Lernziel kann herausgearbeitet und formuliert werden: Wir wollen für ein Quadrat mit einem bestimmten Flächeninhalt die Seitenlänge bestimmen können. Dies ist allgemeiner formuliert als das Halbierungsproblem, aber eine solch allgemeine Formulierung ist durchaus sinnvoll, um das übergeordnete Ziel während des Lernprozesses stets vor Augen zu haben. Wichtig ist hierbei, dass auch das Ziel selbst von den Lernenden verstanden wird und sie jederzeit überprüfen können, inwieweit sie das Ziel schon erreicht haben.

3. Bei der Überlegung, welche Lernhandlungen geeignet sind, sich dem Wurzelbegriff zu nähern, sollen diese aus den fachlich relevanten Zusammenhängen extrahiert und am gewählten Kontext konkretisiert werden:

   • Ein wesentlicher Zusammenhang ist, dass sich Seitenlänge und Flächeninhalt eines Quadrates nicht proportional zueinander verhalten, also eine doppelte Seitenlänge nicht zu einem doppelten Flächeninhalt führt. Dieser nicht-Zusammenhang gilt aber dann natürlich auch umkehrt: Der doppelte Flächeninhalt wird nicht durch eine doppelte Seitenlänge verursacht. Diese Perspektive ist wichtig, um zu erkennen, dass sich Wurzeln unbekannter Zahlen nicht so einfach linear aus Wurzeln bekannter Zahlen konstruieren lassen. Als konkrete Lernhandlung lässt sich die umsetzen, indem zu vorgegebenen Quadraten Seitenlängen und Flächeninhalte bestimmt werden müssen. Die Auswahl sollte derart erfolgen, dass sowohl vielfache Seitenlängen als auch vielfache Flächeninhalte auftreten, damit bei den jeweils anderen Größen erkannt wird, dass diese keine entsprechenden Vielfachen darstellen.

   • Trotz der nicht-Linearität ist die bestehende (strenge) Monotonie ein weiterer Zusammenhang zwischen Seitenlängen und Flächeninhalt. Dieser kann herausgearbeitet werden, indem (nach der vorherigen Erfahrung) Flächeninhalte und Seitenlängen von Quadraten gegeben werden und zwischen diesen eine Zuordnung erfolgen muss. Dies betont den qualitativen Zusammenhang – auch wenn ein konkretes Ausrechnen damit noch nicht möglich ist.

   • Der nächste Handlungsschritt ist nun das näherungsweise Bestimmen von Seitenlängen über das Intervallschachtelungsprinzip. Dieses baut in fachlicher Hinsicht auf die Monotonie auf und es sind nun immer Zahlenpaare \(a_1\) und \(a_2\) gesucht, für die \(a_1^2 \leq A \leq a_2^2\) für einen gegebenen Flächeninhalt \(A\) gilt. Über eine vorstrukturierte (und ggf. auch schon über Beispiele vorausgefüllte) Tabelle kann dieses Vorgehen unterstützt werden. Begleitet werden kann dieses Vorgehen natürlich auch über ein zeichnerisches Nähern, indem den Quadraten weitere einbeschrieben werden, deren Seitenlängen gemessen und daraus der Flächeninhalt berechnet wird.

   Tab. 11.1: Intervallschachtelung zur Bestimmung von \(\sqrt{8}\)

   \(a_1^2\)	\(a_1 \leq \sqrt{8\,\mathrm{cm}^2} \leq a_2\)	\(a_2^2\)
   \(4\,\mathrm{cm}^2\)	\(2\,\mathrm{cm} \leq \sqrt{8\,\mathrm{cm}^2}\leq 3\,\mathrm{cm}\)	\(9\,\mathrm{cm}^2\)
   \(7{,}84\,\mathrm{cm}^2\)	\(2{,}8\,\mathrm{cm} \leq \sqrt{8\,\mathrm{cm}^2}\leq 3\,\mathrm{cm}\)	\(9\,\mathrm{cm}^2\)
   \(7{,}84\,\mathrm{cm}^2\)	\(2{,}8\,\mathrm{cm} \leq \sqrt{8\,\mathrm{cm}^2}\leq 2{,}9\,\mathrm{cm}\)	\(8{,}41\,\mathrm{cm}^2\)
   \(7{,}84\,\mathrm{cm}^2\)	\(2{,}8\,\mathrm{cm} \leq \sqrt{8\,\mathrm{cm}^2}\leq 2{,}85\,\mathrm{cm}\)	\(8{,}1225\,\mathrm{cm}^2\)
   	\(\vdots\)

   All die Handlungen haben gemeinsam, dass dabei zwar an konkreten Quadraten mit bestimmten Flächeninhalten und Seitenlängen agiert wird, allerdings sind sie verallgemeinerbar und in ihrer Ausführung nicht an die genutzen Größen- und Zahlenwerte gebunden. Die mit den Lernhandlungen verbunden Aufgabenstellungen sollten dabei über eine Kernfrage in ihrer Vorschauperspektive begleitet werden. Aus dem Lernziel heraus lässt sich beispielsweise formulieren (siehe Barzel et al., 2016, S. 94): »Warum ist es so schwierig, das Quadrieren rückwärts zu rechnen?«

4. Die etappenweise Verinnerlichung von Handlungen bietet sich insbesondere für die dritte Lernhandlung an (in der die Wurzeln näherungsweise bestimmt werden), da in dieser Handlung alle vorherigen Zusammenhänge integriert sind. Eine materielle bzw. materialisierte Handlung ist schwer zu identifizieren, ggf. noch das Ausmessen der Seitenlänge eines Quadrates. In der sprachlichen Handlung sollte das Vorgehen der Intervallschachtelung von den Schülerinnen und Schülern beschrieben werden. Die geistige Handlung ist dann das Ausführen der Intervallschachtelung selbst (wobei natürlich die errechneten Zahlen notiert werden).

   Die bei der Diskussion der Lernhandlungen dargestellten wesentlichen Begriffseigenschaften müssen nun den Schülerinnen und Schülern über die Verallgemeinerung der Lernhandlungen explizit gemacht werden. Dies kann bspw. im Unterrichtsgespräch erfolgen, indem das Vorgehen am konkreten Beispiel reflektiert und dabei das Allgemeine daran herausgearbeit wird. Es müssen natürlich nicht Begriffe wie nicht-Linearität, Monotonie und Intervallschachtelung genutzt werden, aber deren inhaltliche Aussagekraft muss sichtbar werden. Daraus abgeleitet bietet sich folgende Definition der Wurzel an:

   Die Wurzel einer nichtnegativen Zahl \(A\) ist diejenige nichtnegative Zahl \(a\), für die \(a^2 = A\) gilt.

   Man schreibt: \(a = \sqrt{A}\).

   Beispiel: \(\sqrt{9} = 3\), denn \(3^2 = 9\).

   

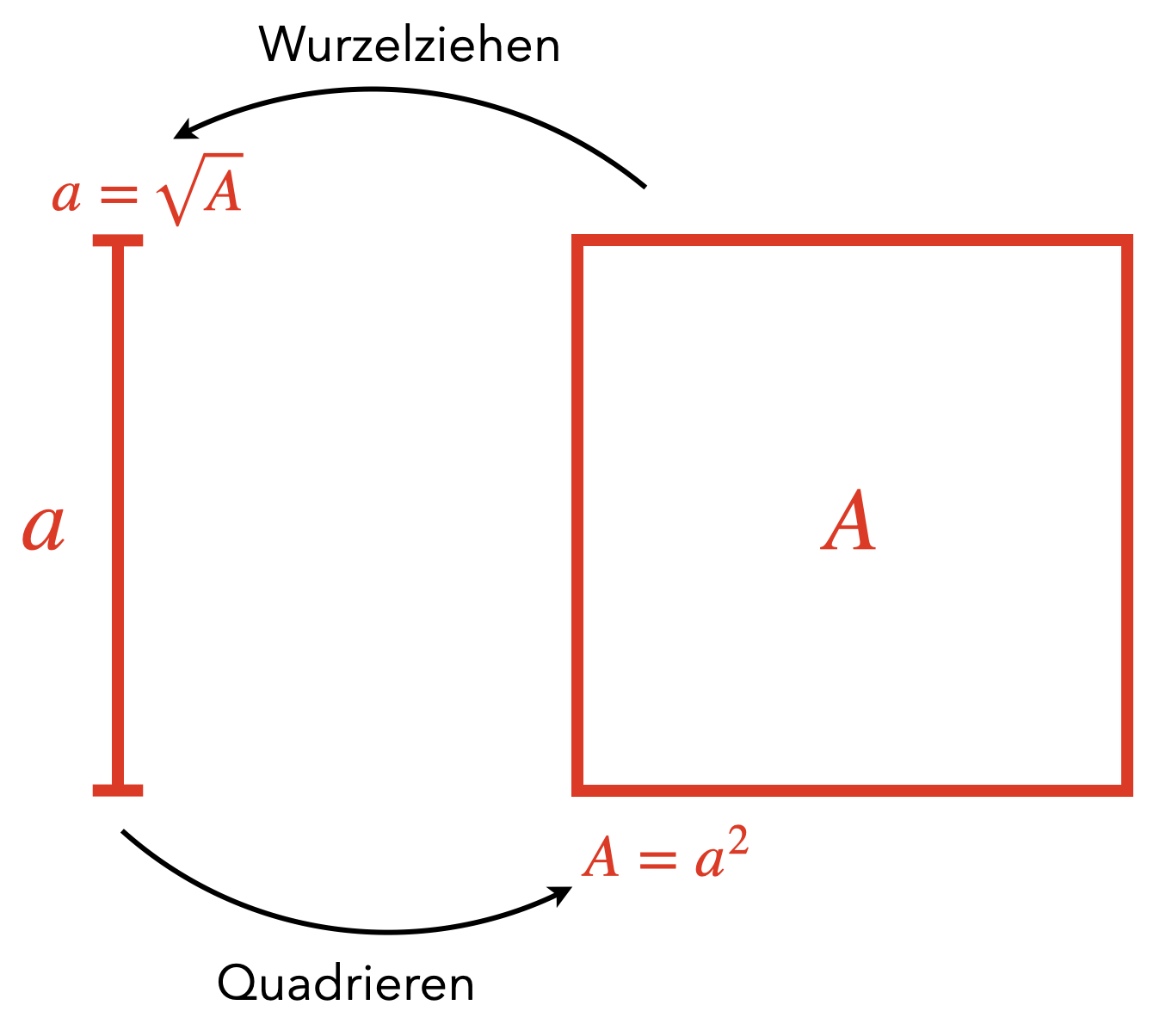
   Abb. 11.2: Veranschaulichung der Wurzel

   Achtung! Es ist zwar \((-3)^2 = 9\), aber \(\sqrt{9} \neq -3\), da \(-3\) negativ ist. Außerdem ist \(\sqrt{-9}\) nicht definiert, da \(-9\) negativ ist.

   Die Auswahl des Beispiels \(\sqrt{9}=3\) war dabei nicht zufällig. Als Einstiegsbeispiel sollte ein leicht nachvollziehbares gewählt werden, daher sollte es sich um (möglichst kleine) natürliche Zahlen handeln und nicht mit Einheiten agiert werden. \(\sqrt{0}\) und \(\sqrt{1}\) fallen weg, da dies Spezialfälle sind, in denen die Werte für Wurzel und Quadrat identisch sind. \(\sqrt{4}\) ist ebenfalls ungünstig, weil dann bei der Erklärung der Umkehrung \(2^2 = 4\) die Ziffer \(2\) doppelt (und in verschiedenen Funktionen) auftaucht, nämlich als Basis und als Exponent. Um derartige Anfangsverwirrungen zu vermeiden, ist dann \(\sqrt{9}\) das nächstliegende Einstiegsbeispiel. Entsprechend dem Kontrastprinzip müssen auch nahe Gegenbeispiele wie \(\sqrt{-9}\) sowie \(\sqrt{9}\neq -3\) gebracht werden. Das Variationsprinzip für die Auswahl von Beispielen kann über die verschiedenen Quadrate am Ausgangskonkretum erfüllt werden, in dem dort etwa nicht nur natürliche Zahlen auftreten.

5. Anschließend erfolgen vertiefende Übungen und die Betrachtung weiterer Zusammenhänge, anhand derer das Begriffsverständnis vertieft wird.

   • Beim Wurzelbegriff geht dies insbesondere mit der Zahlbereichserweiterung in die reellen Zahlen einher. Dabei werden Wurzeln als Zahlen (und nicht Seitenlängen) aufgefasst und bspw. auch auf dem Zahlenstrahl geordnet.

   • Eine weitere Anwendung ist die Behandlung der Wurzelgesetze, bspw. \(\sqrt{x\cdot y} = \sqrt{x}\cdot \sqrt{y}\). Bezieht man sich beim Wurzelziehen auf das Umkehren des Quadrierens, so ist eine Begründung mithilfe des Potenzgesetzes \(x^2\cdot y^2 = (x\cdot y)^2\) möglich.

11.2.3 Heron-Verfahren

Die Bildungsstandards erfordern die Implementation eines algorithmischen Verfahrens zur Bestimmung von Quadratwurzeln (Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, 2022a, S. 16), wofür neben der Intervallschachtelung auch das Heron-Verfahren geeignet ist

Die Idee hinter dem Heron-Verfahren besteht darin, dass ein Rechteck mit Flächeninhalt \(A\) immer mehr zu einem Quadrat mit Flächeninhalt \(A\) überführt wird, dessen Seitenlänge zu bestimmen ist.

• In einem ersten Schritt kann eine Seitenlänge \(x_1\) festgelegt und daraus die zweite Seitenlänge \(y_1 = \cfrac{A}{x_1}\) bestimmt werden.
  
• Um die Seitenlängen anzugleichen wird in einem nächsten eine neue Seitenlänge \(x_2\) als Durchschnitt der vorherigen Seitenlängen bestimmt: \(x_2 = \cfrac{x_1+y_1}{2}\). So wird sichergestellt, dass das neue Rechteck quadratischer als das alte ist. Für die zweite Rechtecksseite gilt entsprechend \(y_2 = \frac{A}{x_2}\).
• Dieses Vorgehen wird nun beliebig weitergeführt, sodass stets gilt: \(x_{n+1} = \cfrac{x_n+y_n}{2} = \cfrac{x_n+\frac{A}{x_n}}{2} = \cfrac{1}{2}\left(x_n + \cfrac{A}{x_n}\right)\)

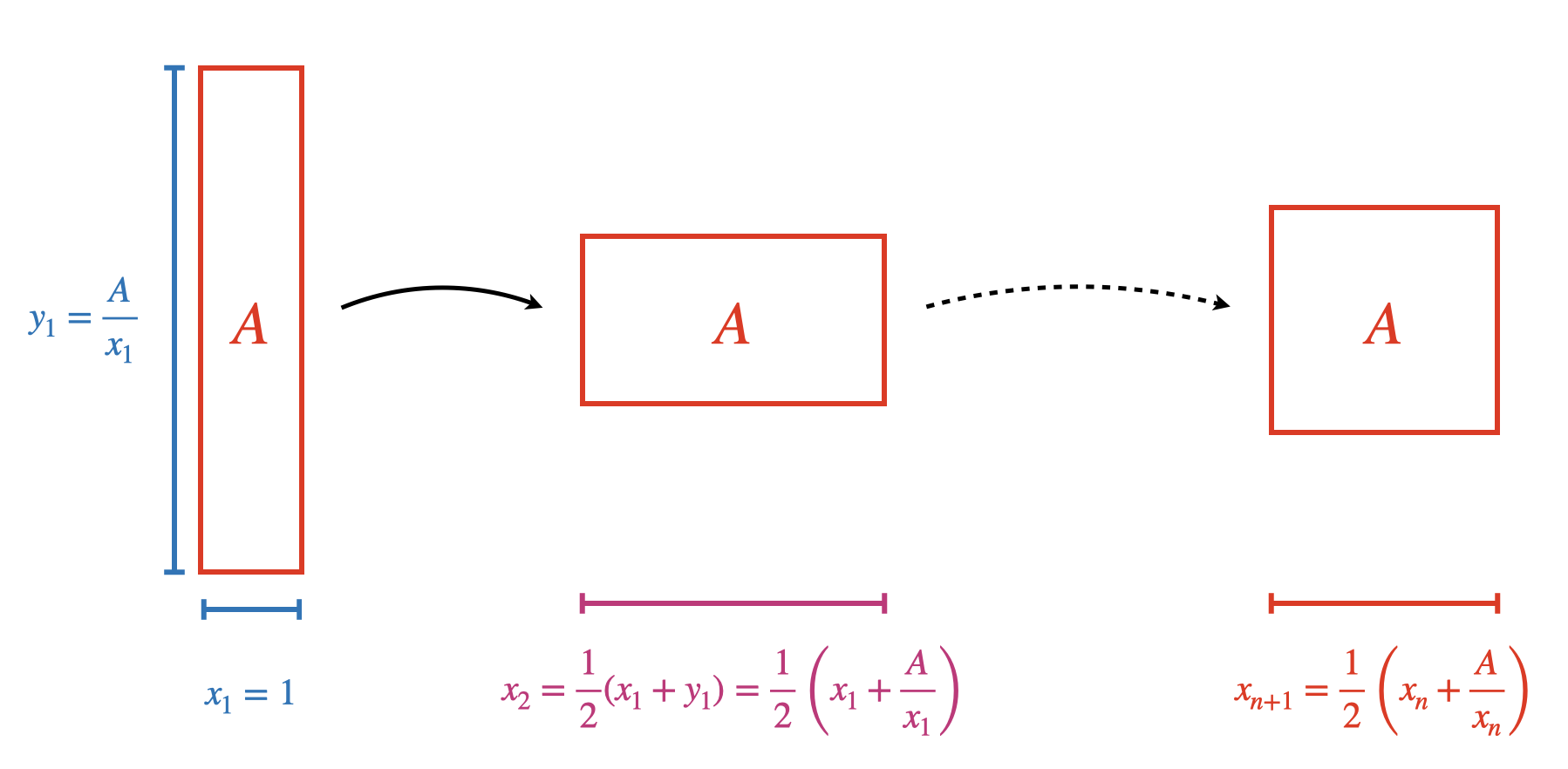
Abb. 11.3: Visualisierung des Heron-Verfahrens

Mit einem Startwert von bspw. \(x_1 = 1\) ergibt sich als rekursive Bildungsvorschrift für das Heron-Verfahren:

\[x_1 = 1; \quad x_n = \cfrac{1}{2}\left(x_n + \cfrac{A}{x_n}\right)\]

Einen Beweis der Konvergenz dieser Folge sollten Sie aus Ihren Analysis-Veranstaltungen kennen. Eine schrittweise Betrachtung des Folgenverhaltens kann über eine Tabellenkalkulation erfolgen, siehe Abbildung 11.4.

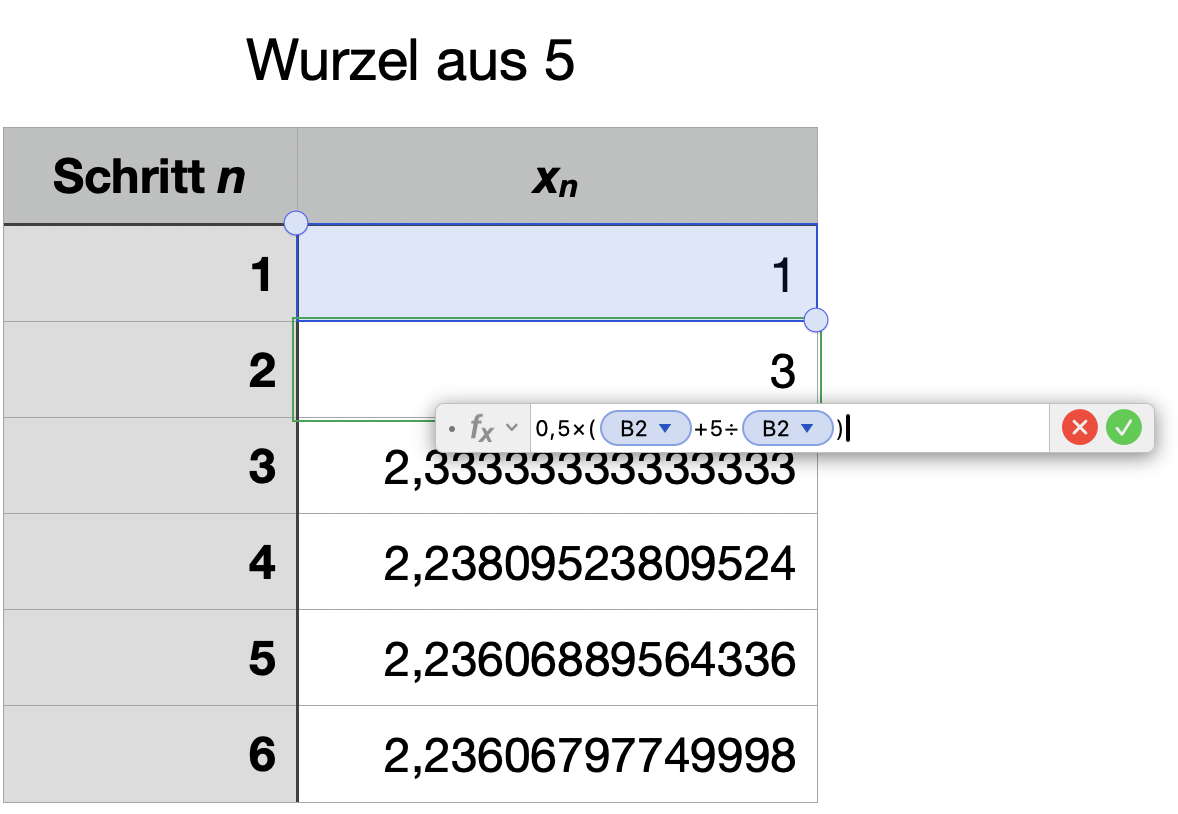
Abb. 11.4: Heron-Verfahren in einer Tabellenkalkulation

Eine Implementation in einen Algorithmus bedarf weiterhin einer Abbruchbedingung. Dies ist bspw. darüber möglich, dass der Abstand aufeinander folgender Ergebnisse einen bestimmten Wert unterschreiten soll, also \(|x_{n+1}-x_n|<\varepsilon\) für ein vorher festgelegtes \(\varepsilon\) gelten muss. Ein exemplarischer Code für \(\sqrt{5}\) mit einer Genauigkeit von 4 Dezimalstellen sieht folgendermaßen aus:

A = 5
x = 1
eps = 0.0001
while(abs(x - (x+A/x)/2) > eps){
  x = (x+A/x)/2
}

References

Barzel, B., Hußmann, S., Leuders, T., & Prediger, S. (Hrsg.). (2016). Mathewerkstatt. 9, Schulbuch (Mittlerer Schulabschluss, allgemeine Ausg., 1. Aufl.). Cornelsen.

Padberg, F., & Benz, C. (2021). Didaktik der Arithmetik: fundiert, vielseitig, praxisnah (5., überarbeitete Aufl.). Springer Spektrum.

Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland. (2022a). Bildungsstandards für das Fach Mathematik Erster Schulabschluss (ESA) und Mittlerer Schulabschluss (MSA). (Beschluss der Kultusministerkonferenz vom 15.10.2004 und vom 04.12.2003, i.d.F. vom 23.06.2022). https://www.kmk.org/fileadmin/Dateien/veroeffentlichungen_beschluesse/2022/2022_06_23-Bista-ESA-MSA-Mathe.pdf

Weigand, H.-G., Schüler-Meyer, A., & Pinkernell, G. (2022). Didaktik der Algebra: nach der Vorlage von Hans-Joachim Vollrath. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-64660-1

---

31. Mehr zu diesen Begriffen siehe im Kapitel 6.1 des Skripts von 2021/22 zur Stoffdidaktik Mathematik↩︎

32. Dies wird bei höheren Exponenten sogar noch bedeutsamer: Dort ist \((-3)^3 = -27\). Die Gleichung \(x^3 = -27\) ist im Reellen sogar eindeutig lösbar (im Komplexen dagegen hat sie drei Lösungen), aber \(\sqrt[3]{-27}\) ist nicht definiert. Gerade, weil einige Taschenrechner fälschlicherweise die dritte Wurzel aus \(-27\) mit \(-3\) angeben, muss auf eine derartige Gefahr eingegangen werden, wenn Wurzeln höherer Exponenten behandelt werden. Dies zeigt einmal mehr, dass Sie als Lehrkraft über den aktuellen Unterrichtsstoff (z. B. Quadratwurzeln) hinausdenken müssen (z. B. Kubikwurzeln), um Rückschlüsse ziehen zu können, welche inhaltlichen Besonderheiten zu betonen sind.↩︎

33. Die fachmathematische Grundlage hierfür ist, dass Cauchy-Folgen in den reellen Zahlen immer konvergieren und sich die nichtnegative Lösung der Gleichung \(x^2 = a\) mit \(a\geq 0\) über eine rationale Cauchy-Folge nähern lässt – konkret mit dem Heron-Verfahren.↩︎

34. Hier lohnt es sich übrigens, auf die Wortherkunft einzugehen und zu begründen, warum Radieschen als solche bezeichnet werden.↩︎