5 Arbeitsmittel

Ziele

  • Sie können Arbeitsmittel über Anschaulichkeit, Abstraktheit und Operierbarkeit charakterisieren.
  • Sie kennen einen Ablauf zur Ausbildung von Grundvorstellungen mithilfe von Arbeitsmitteln. Dabei sind Sie sich der besonderen Bedeutung des Sprechens über Handlungen bewusst.
  • Sie können lerntheoretisch den Einsatz von Arbeitsmitteln bei der Aneignung von Lerngegenständen über Internalisierungs- und Externalisierungsprozesse erläutern.

Material

Einer der Aspekte der Grundvorstellungsidee ist die Sinnkonstituierung durch Handlungsbezug (siehe Definition 4.1). Sollen Grundvorstellungen bei Schülerinnen und Schülern ausgebildet werden, ist es notwendig, diese Handlungen zu verinnerlichen. Besonders hilfreich hat sich hierfür der Einsatz von Arbeitsmitteln herausgestellt, anhand derer gehandelt wird. Auf tätigkeitstheoretischer Ebene wird der Begriff der Handlungen in den Kapiteln 8 und 8.3 nochmals genauer diskutiert. An dieser Stelle soll – zunächst bezogen auf die Tätigkeitstheorie – die Bedeutsamkeit von Werkzeugen für die Aneignung von Lerngegenständen beschrieben werden und anschließend erfolgt – unter Bezugnahme auf mathematikdidaktische Quellen – eine Begriffsklärung für Arbeitsmittel.

5.1 Aneignung von Lerngegenständen

5.1.1 Vermittelnde Werkzeuge

Nach Wygotski (1985) erfolgt eine Interaktion eines Individuums mit einem Lerngegenstand niemals direkt, sondern geschieht stets über ein vermittelndes Werkzeug. Es kann sich dabei um echte Werkzeuge wie Maschinen, Geräte und andere Hilfsmittel handeln, aber auch Gesten, die Sprache, Abbildungen und Skizzen oder ähnliches sind in dem Sinne als Werkzeug zu verstehen. Entscheidend ist, dass dieses vermittelnde »Ding« für das Individuum die Funktion eines Vermittlers erfüllt. Daher wird auch von einem psychischen Werkzeug gesprochen.

Durch die Nutzung eines geeigneten Werkzeugs ist das Individuum damit einerseits in der Lage, seine Kenntnisse, Fähigkeiten und Fertigkeiten zu externalisieren, d. h. das Werkzeug zielgerichtet so einzusetzen, dass auf den Lerngegenstand eingewirkt werden kann. Andererseits kann das Werkzeug auch dabei helfen, Eigenschaften des Lerngegenstands zu internalisieren, indem die Werkzeugnutzung dazu führt, dass das Individuum Kenntnisse, Fähigkeiten und Fertigkeiten über den Lerngegenstand gewinnt. Um sich also einen Lerngegenstand anzueignen, sind sowohl stets Externalisierungs- als auch Internalisierungsprozesse notwendig. Man kann auch sagen, dass Aneignung als Einheit aus Externalisierung und Internalisierung aufzufassen ist.

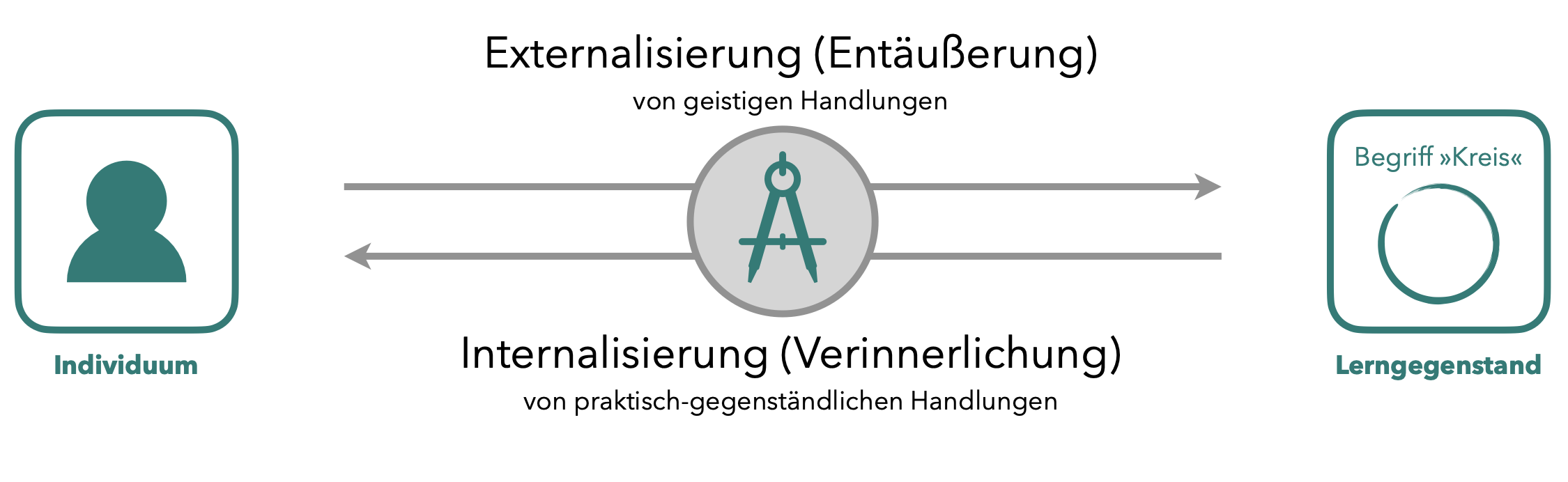
Werkzeuge als Vermittler in der Tätigkeitstheorie am Beispiel des Kreises

Abb. 5.1: Werkzeuge als Vermittler in der Tätigkeitstheorie am Beispiel des Kreises

5.1.2 Zur Rolle des Sprechens

Eine wichtige Rolle beim Aneignen spielt das Sprechen über die durchgeführten Handlungen. Dieses dient quasi als Bindeglied zwischen geistiger Handlung und praktisch-gegenständlicher Handlung, da es sowohl den Externalisierungsprozess unterstützt (das Geistige muss über das Sprechen externalisiert werden) als aus der Internalisierung dienlich ist (über das Sprechen wird das Praktisch-Gegenständliche psychisch verarbeitet). Damit unterstützt das Sprechen auch eine schrittweise Abkehr vom externen Werkzeug und damit eine geistige Durchdringung des betrachteten Lerngegenstands. Abbildung 5.2 zeigt eine entsprechende Schrittfolge zum Aufbau von Grundvorstellungen, wie sie Wartha & Schulz (2011, S. 11) vorschlagen (wobei die dort verwendeten Farben nichts mit den hier im Skript genutzten Farben für die vier Ebenen zu tun haben).

Aufbau von Grundvorstellungen nach Wartha & Schulz (2011, S. 11)

Abb. 5.2: Aufbau von Grundvorstellungen nach Wartha & Schulz (2011, S. 11)

In Abschnitt 8.3.2 wird diese Sichtweise noch einmal tätigkeitstheoretisch eingeordnet und in Kapitel 9 hinsichtlich der verschiedenen Arten mathematischen Wissens (Begriffe, Sachverhalte und Verfahren) konkretisiert.

5.1.3 Lernmittel und Lernmodelle

Im Zusammenhang mit Lernprozessen werden nun (ggf. psychische) Werkzeuge auch als Lernmittel bezeichnet und können entsprechend vielfältiger Natur sein, z. B.:

  • Mithilfe eines Zirkels können Kreise erzeugt werden, indem der Zirkel seiner Funktion entsprechend verwendet wird (Externalisierung der Kenntnisse über den Kreis). Die Gestaltung und Handhabung des Zirkels selbst vermittelt jedoch auch Wissen über den Kreisbegriff, so dass dieses in der Verwendung des Werkzeugs aufgebaut werden kann (Internalisierung des Wissens über den Kreis).
  • Die digitale Stellenwerttafel ermöglicht es, das Stellenwertverständnis zu Zahlen aufzubauen und Zahlen entsprechend darzustellen. Durch das Verhalten der Anwendung (dass z. B. ein Plättchen beim Verschieben von der Zehner- in die Einer-Spalte automatisch entbündelt wird) unterstützt diesen Aneignungsprozess (siehe Kortenkamp et al., 2018).
  • Auch Aufgaben haben die Funktion eines (bedeutsamen!) Lernmittels, wenn sie als Aufforderung zum Lernhandeln aufgefasst werden. An ihnen erarbeiten sich die Schülerinnen und Schüler bestimmte Elemente des Lerngegenstands und die Gestaltung der Aufgabe sowie die vorhandenen Kenntnisse der Schülerinnen und Schüler bestimmen den Verlauf und Erfolg der Lernhandlung.

Als weiteres Unterstützungsinstrument und damit spezifisches Lernmittel dient in der Tätigkeitstheorie das Konzept des Lernmodells. Lernmodelle sind »sinnliche Stützen geistigen Handelns« (Giest & Lompscher, 2006, S. 225) und können bspw. Zeichnungen, strukturierte Darstellungen, digitale Anwendungen usw. sein. Sie haben als Modelle dabei den Vorteil, dass sie »nicht die konkreten Merkmale der einzelnen Erscheinungen oder Situationen, sondern nur konstitutive, im gegebenen Kontext wesentliche Merkmale und Relationen enthalten, also abstrakt sind« (Lompscher, 1983, S. 64, Hervorhebung im Original). Gleichzeitig sind sie aber auch »anschauliche Abbildungen und machen damit die grundlegenden Zusammenhänge und Wesensmerkmale der Wahrnehmung und Vorstellung zugänglich« (Lompscher, 1983, S. 64, Hervorhebung im Original).

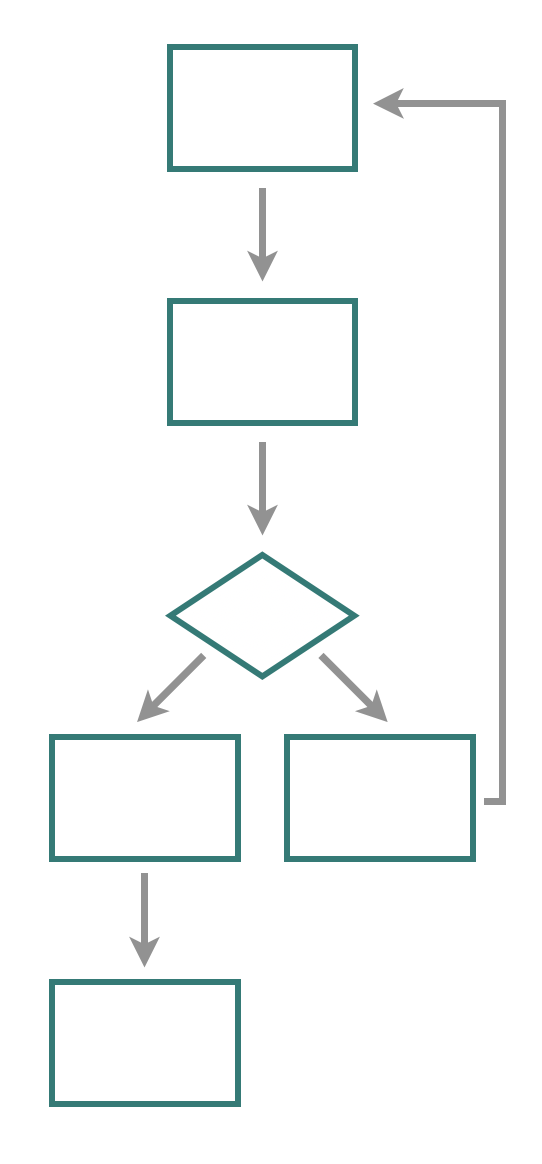
Beispiel eines Lernmodells für die Bestandteile eines Algorithmus

Abb. 5.3: Beispiel eines Lernmodells für die Bestandteile eines Algorithmus

Lernmodelle können daher insbesondere für mathematische Lerngegenstände dienlich sein, da sie die »abstrakte Struktur des Gegenstands zusammen mit dem prinzipiellen Weg [..], der zur Aufdeckung der Struktur geführt hat«, beinhalten (Lompscher, 1996, S. 6). Dass es sich dabei nicht ausschließlich um Abbildungen, sondern eben auch haptische Materialien oder digitale Anwendungen handeln kann, machen die obigen und noch folgenden Beispiele deutlich.

5.2 Begriffsklärung Arbeitsmittel

Die Begriffe Lernmittel und Lernmodell als tätigkeitstheoretisch geprägte Konzepte werden in der aktuellen Mathematikdidaktik kaum verwendet. Verbreiteter ist dagegen der Begriff des Arbeitsmittels. Nach Krauthausen (2018, S. 310) sind Arbeitsmittel im Mathematikunterricht Veranschaulichungsmittel (zum Illustrieren oder Visualisieren mathematischer Konzepte) oder Anschauungsmittel (d. h. »Darstellungen mathematischer Ideen in der Hand der Lernenden […] zur (Re-)Konstruktion mathematischen Verstehens«). Entscheidend ist hierbei eine »aktivistische« Sichtweise, also dass die Schülerinnen und Schüler die Arbeitsmittel aktiv als »Denkwerkzeug« verwenden. Die Aufgabe der Lehrkraft ist es dabei, »in den sachgerechten Gebrauch ein[zu]führen und Hilfen (zur Selbsthilfe) im Umgang mit Anschauungsmitteln [zu] gewähren« (Krauthausen, 2018, S. 310). Reinhold et al. (2023, S. 5251) formulieren in inhaltlich ähnlicher Weise: »Arbeitsmittel im Mathematikunterricht repräsentieren mathematische Objekte und erlauben Handlungen mit den dargestellten Objekten.«12

In dieser Einordnung übernehmen Arbeitsmittel demnach die Aufgabe eines Lernmittels (auch wenn es weitere Lernmittel gibt, die keine Arbeitsmittel sind). In der obigen Aufzählung der Beispiele kann die digitale Stellenwerttafel als Arbeitsmittel aufgefasst werden.

Als Definition für Arbeitsmittel, die sowohl mathematikdidaktische als auch tätigkeitstheoretische Bezüge aufgreift, wird im Folgenden gewählt:

Definition 5.1 (Arbeitsmittel) Ein Arbeitsmittel ist eine materielle oder materialisierte13 sowie durch die Schülerinnen und Schüler operierbare Repräsentation eines Lerngegenstands. Damit muss ein Arbeitsmittel folgende Bedingungen erfüllen:

  • Es enthält die dem Wesen des Lerngegenstands entsprechenden Merkmale und Relationen (Abstraktheit).
  • Es macht die dem Lerngegenstand zugrundeliegende Struktur der Wahrnehmung und Vorstellung zugänglich (Anschaulichkeit).
  • Es ermöglicht, Lernhandlungen durchzuführen, die der Aneignung des Wesens des Lerngegenstands dienlich sind (Operierbarkeit).

Bei der Auswahl (oder Entwicklung) eines Arbeitsmittels ist es für Sie als Lehrkraft daher von besonderer Bedeutung, was der Kern des entsprechenden mathematischen Gegenstands ist. Hierfür ist es notwendig, dass also das Arbeitsmittel mit der Kernidee des Lerngegenstands in Einklang steht – mehr dazu finden Sie hinsichtlich der konkreten Ebene des Vier-Ebene-Ansatzes im nächsten Kapitel. Bezugnehmend auf die Grundvorstellungsidee auf der semantischen Ebene ermöglicht das Arbeitsmittel nun auch operatives Handeln in Bezug auf (visuelle) Repräsentationen und unterstützt damit auch den zweiten Aspekt von Definiton 4.1.

5.3 Beispiel Äquivalenzumformungen

Bevor Arbeitsmittel für Äquivalenzumformungen von Gleichungen untersucht werden, ist es zunächst notwendig, auf der formalen und semantischen Ebene zu klären, was Gleichungen sind und was man sich unter diesen vorstellen kann.

5.3.1 Der Gleichungsbegriff

Offensichtlich handelt es sich bei dem Ausdruck \(2+ 3 = 5\) um eine Gleichung. Auch der Ausdruck \(2 + 3 = 8\) stellt eine Gleichung dar – jedoch eine falsche Aussage. Relevant ist bei beiden Ausdrücken, dass zwei Terme durch ein Gleichheitszeichen miteinander verbunden sind. Über den Wahrheitsgehalt einer solchen Gleichung kann jedoch nicht immer eine Aussage getroffen werden. Betrachtet man etwa \(2x = 14\), so kann es sich dabei um eine wahre Aussage (für \(x=7\)) oder um eine falsche Aussage (für \(x\neq 7\)) handeln. In dem Fall spricht man also von einer Aussageform, die erst durch Einsetzen der Variable zu einer Aussage wird.

Zusammenfassend gilt: Eine Gleichung ist eine Aussageform, in der zwei Terme \(T_1(x)\) und \(T_2(x)\) durch ein Gleichheitszeichen miteinander verbunden werden: \(T_1(x) = T_2(x)\) (vgl. Weigand et al., 2022, 242 ff.)

Liegt eine Gleichung als Aussageform vor, z. B. \(\frac{7}{x} = 2\), interessiert in der Regel die Lösung der Gleichung, also \(x = 3,\!5\). Ob eine solche Lösung existiert, hängt jedoch von der Grundmenge ab, in der die Aussageform betrachtet wird. Wird für die Gleichung \(\frac{7}{x} = 2\) als Grundmenge \(\mathbb{Z}\) festgelegt, so ist sie nicht lösbar. Ist dagegen \(\mathbb{Q}\) die Grundmenge, so kann eine Lösung angegeben werden. Die Grundmenge entspricht in der Regel dem zur Verfügung stehenden Zahlbereich. Dagegen beschreibt die Definitionsmenge diejenige Teilmenge der Grundmenge, für die die Aussageform überhaupt definiert ist – im obigen Fall also \(\mathbb{Z}\backslash\{0\}\). Die Menge aller Lösungen, für die die Ausageform eine wahre Aussage ergibt, wird dann als Lösungsmenge bezeichnet und ist demnach wiederum eine Teilmenge der Definitionsmenge.

Weigand et al. (2022, S. 257) unterscheiden in vier Grundvorstellungen zu Gleichungen:

  • Operationale Grundvorstellung. Gleichung als Ausdruck einer Berechnung oder Umformung, z. B. \(2+3 = 5\) oder \(V = \frac{1}{3}\pi r^2 h\).
  • Relationale Grundvorstellung. Gleichung als Anlass, Zahlen oder Terme zu ermitteln, für die beide Seiten der Gleichung denselben Wert besitzen, z. B. \(2x +1 = 7\).
  • Funktionale Grundvorstellung. Gleichung als Ausdruck eines Vergleichs zwischen zwei Funktionstermen, z. B. \(x+1 = -3x\).
  • Objekt-Grundvorstellung. Gleichung als ein Objekt, das charakteristische Eigenschaften hat, z. B. \(x^2 +y^2 = r^2\) als Kreisgleichung.

Innerhalb dieser Grundvorstellungen kann nun das Lösen von Gleichungen unterschiedlich interpretiert werden. In der operationalen Grundvorstellung bietet sich bspw. ein Rückwärtsrechnen an, in der funktionalen Grundvorstellung die Schnittpunktbestimmung in einem Diagramm, in dem beide Terme als Funktionsgraphen dargestellt werden. In der Objekt-Grundvorstellung kann das Überprüfen der Passung von Koordinaten zum (ggf. teilweise) Lösen der Gleichung führen, während sich in der relationalen Grundvorstellung Äquivalenzumformungen anbieten.

Für letzteres ist es zunächst notwendig zu klären, was unter der Äquivalez von Gleichungen zu verstehen ist. Einerseits ist dies über eine Lösungsmengenäquivalenz möglich, d. h. zwei Gleichungen (mit derselben Grundmenge) heißen lösungsmengenäquivalent zueinander, wenn sie dieselbe Lösungsmenge besitzen. Die ist etwa bei den Gleichungen \(2x+ 1 = 7\) und \(2x + 3 = 9\) offensichtlich mit der Lösungmenge \(\{3\}\). Jedoch besitzen auch die Gleichungen \(|\mathrm{e}^{\mathrm{i}x}| = 1\) und \(\sin(x) = 0\) dieselbe Lösungsmenge, obwohl die beiden Gleichungen nicht durch offensichtliche Umformungen ineinander übergeführt werden können. Es bietet sich daher auch an, eine Umformungsäquivalenz zu definieren, von der man spricht, wenn zwei Gleichungen durch Äquivalenzumformungen ineinander übergeführt werden können. Letztere wiederum ergeben sich, wenn auf beide Seiten der Gleichungen eine eineindeutige, also injektive Funktion angewandt wird, da diese nicht die Lösungsmenge der Gleichung ändert.14 Dabei sind die Addition, Subtraktion, Multiplikation und Division (bis auf Division durch Null) derartige injektive Funktionen, also Äquivalenzumformungen. Das Quadrieren einer Gleichung dagegen erhält im Allgemeinen nicht die Lösungsmenge, da die Funktion \(^2: x \mapsto x^2\) nicht injektiv ist.

5.3.2 Umformungen verstehen

Um Äquivalenzumformungen nachvollziehen zu können, haben sich für den Mathematikunterricht verschiedene Unterstützungsinstrumente etabliert. Diese sollen nun kurz vorgestellt und hinsichtlich ihrer Eignung als Arbeitsmittel (also inwiefern sie die Kriterien aus Definiton 5.1 erfüllen) untersucht werden. Die folgenden Betrachtungen beziehen sich ausschließlich auf lineare Gleichungen mit einer Variablen.

5.3.2.1 Waage-Modell

Im Waage-Modell werden Gleichungen über Massestücke auf einer Balkenwaage dargestellt, wobei i. d. R. absolute Werte in anderer Größe oder Form dargestellt werden als die Variable. Die Gleichheit wird visualisiert über das Gleichgewicht der Waage, also dass deren Balken horizontal ausgerichtet ist.

Eine Äquivalenzumformung besteht nun darin, in beiden Waagschalen dieselbe Operation durchzuführen, so dass die Waage stets im Gleichgewicht bleibt.

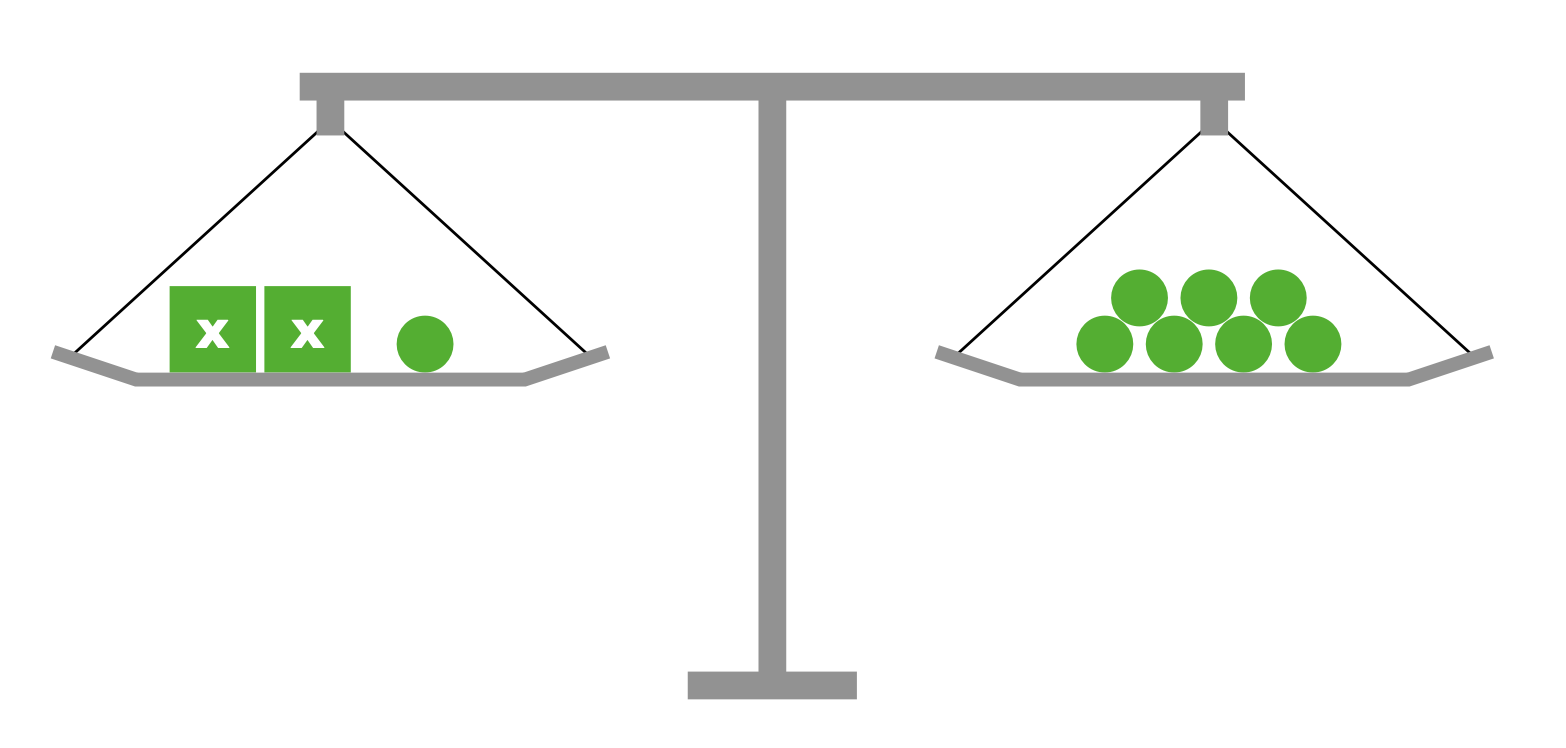
Waage-Modell für die Gleichung $2x+1 = 7$

Abb. 5.4: Waage-Modell für die Gleichung \(2x+1 = 7\)

Ein Vorteil besteht in der hohen Anschaulichkeit des Modells. Auch die Operierbarkeit ist für Gleichungen mit natürlichen Vorfaktoren und ausschließlich Summen gegeben. Hier zeigen sich aber auch schon erste Schwächen. Nach Weigand et al. (2022, 260 f.) bestehen folgende weitere Hürden und Herausforderungen:

  • Negative Zahlen können kaum sinnvoll dargestellt werden. Hier gäbe es etwa die Möglichkeit, dass z. B. \(x-1\) als ein Massestück für \(x\) mit einem Loch der Größe \(1\) dargestellt wird. Auch ermöglichen digitale Umsetzungen, dass negative Werte eine Bewegung der Waage entgegen der Schwerkraft bewirken. So kann aber nicht mehr an die Handlungserfahrungen mit echten Balkenwaagen angeknüpft werden, in denen das Modell eigentlich seinen Ursprung hat.

  • Gleichzeitig muss auch zugegeben werden, dass nur noch wenige Schülerinnen und Schüler tatsächlich Erfahrungen mit Balkenwaagen haben. Der Waagetyp ist einerseits unüblich, andererseits auch sehr empfindlich gegenüber kleinen Masseabweichungen. Es ist also in der praktischen Ausführung recht kompliziert, ein Gleichgewicht herzustellen. Außerdem muss, damit das Gleichgewicht jederzeit bestehen bleibt, auf beiden Seiten gleichzeitig operiert werden.

  • Um die Ausgangssituation der gleichgewichteten Waage herzustellen, muss bereits bekannt sein, über welche Masse das \(x\) repräsentierende Massestück verfügt. Wird also die Situation nicht vorgegeben, erscheint das Lösen unnötig. Außerdem bestünde in der Realität die Möglichkeit, durch Versuch und Irrtum die Masse von \(x\) mit der Waage zu bestimmen, so dass Äquivalenzumformungen ggf. nicht notwendig erschienen und das Vorgehen noch nicht einmal dem Einsetzen verschiedener Werte für \(x\) in die Gleichung entspräche (was einem innermathematischen Versuchen entspräche).

  • Hinzu kommt, dass das Dividieren zunächst mit einem Bündeln und dann einem Wegnehmen einhergeht. Dies weist (in der äußeren Handlung) Ähnlichkeiten zum Subtrahieren auf, was es jedoch nicht ist.

All diese Einschränkungen und mögliche »Reparaturen« des Modells bzw. des Umgangs mit ihm lassen darauf deuten, dass die Abstraktheit des Modells zu gering ist, es also nicht in ausreichendem Maße das Wesen des Lerngegenstand darstellen kann. Der Drang, nicht mögliche Operationen in das anschauliche Modell zu »pressen«, spricht dafür, dass das Modell auf mathematischer Ebene nicht geeignet genug erscheint, um die Anforderungen an die obige Arbeitsmittel-Definition zu erfüllen.

Dies soll jedoch nicht bedeuten, dass das Modell keinesfalls genutzt werden darf. Barzel & Holzäpfel (2011, S. 7) empfehlen, »das Waage-Modell für den Einsatz mit natürlichen Zahlen auf jeden Fall zu nutzen, um das Prinzip der Äquivalenzumformungen zu erläutern.« Dabei sollten die Grenzen des Modell deutlich gemacht werden und anschließend entweder innermathematisch oder mit alternativen Modellen weitergearbeitet werden.

5.3.2.2 Streichholzschachtel-Modell

Eine weitere Möglichkeit bietet das Streichholzschachtel-Modell, bei denen \(x\) die Anzahl der Streichhölzer in einer Schachtel beschreibt, die Gleichung entsprechend mit Schachteln und einzelnen Streichhölzern dargestellt und dann ähnlich wie beim Waage-Modell über gleichartiges Operieren auf beiden Seiten gelöst wird.

Streichholzschachtel-Modell für die Gleichung $2x+1 = 7$

Abb. 5.5: Streichholzschachtel-Modell für die Gleichung \(2x+1 = 7\)

Gegenüber dem Waage-Modell bietet dieses Modell eine einfachere Zugänglichkeit (v. a. in der tatsächlichen Unterrichtssituation) und die Anzahl der Hölzer pro Schachtel ist tatsächlich unbekannt. Jedoch muss man einerseits darauf vertrauen, dass in allen Schachteln dieselbe Anzahl an Streichhölzern vorhanden ist und auch die Gleichheit beider Seiten kann nicht (wie z. B. durch die ausgeglichene Waage) visualisiert werden. In dem Sinne ist die Anschaulichkeit etwas geringer, die Operierbarkeit für die Schülerinnen und Schüler etwas besser als beim Waage-Modell.

Hinsichtlich der Abstraktheit sind keine Unterschiede zu verzeichnen: Es ist weiterhin nur eine Bearbeitung mit natürlichen Vorfaktoren und Variablen sinnvoll möglich.

Barzel & Holzäpfel (2011, S. 6) betonen, dass Streichholzschachteln, Plättchen oder Dosen bereits beim Aufstellen von Termen geeignete Visualisierungsinstrumente sind. Insofern bietet dieses Modell eine gute Anschlussfähigkeit zu vorherigen Erfahren.

5.3.2.3 Strecken-/Pfeil-Modell

Weigand et al. (2022, 261 f.) beschreibt ein Modell, in dem die beiden Terme einer Gleichung über zwei Strecken dargestellt werden, jeweils zusammengesetzt aus Repräsentanten für die Variablen und für die absoluten Werte. Die Gleichheit zeigt sich dann über die gleiche Länge der Strecken. Eine Verallgemeinerung zu Pfeilen ist möglich und wird unten noch diskutiert.

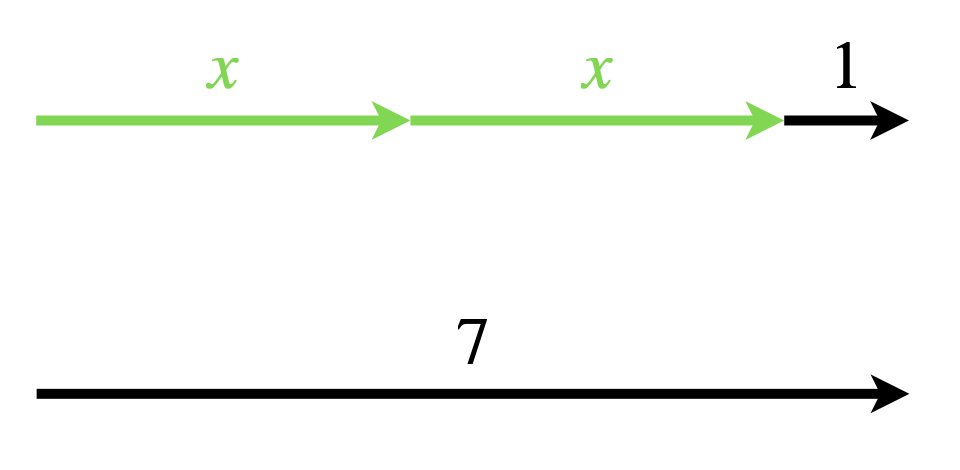
Pfeil-Modell für die Gleichung $2x+1 = 7$

Abb. 5.6: Pfeil-Modell für die Gleichung \(2x+1 = 7\)

Äquivalenzumformungen sind nun über gleichzeitiges Abziehen oder Hinzufügen bzw. Auftrennen von (Teil-)Strecken visualisierbar. Dieses Modell greift offensichtlich nicht auf derart enaktive Erfahrungen zurück, wie es das Waage- oder Streichholzschachtel-Modell tun. Dennoch erfüllt es das Kriterium der Anschaulichkeit, weil es die dem Lerngegenstand zugrundeliegende Struktur der Wahrnehmung und Vorstellung zugänglich macht. Die Operierbarkeit ist für gedankliche Operationen und, wenn die Strecken z. B. über Papierstreifen realisiert werden, auch in Form von real durchgeführten Operationen möglich. Eine digitale Umsetzung des Modells kann bspw. die Operierbarkeit erhöhen und zu einer virtuell-enaktiven Handlungsoption führen.

Ein großer Vorteil des Modells liegt jedoch in der Abstraktheit:

  • So sind gleichermaßen natürliche wie (positive) gebrochenrationale Vorfaktoren visualisierbar, was sich nur in der Länge der (Teil-)Strecken auswirkt.

  • Auch negative Vorfaktoren können über Pfeile in die Gegenrichtung repräsentiert werden. Eine solche Darstellung ist im Umgang mit der Zahlengeraden bekannt, kann auch bei Termen wieder aufgegriffen und hier nun zum Lösen von Gleichungen weiter genutzt werden.

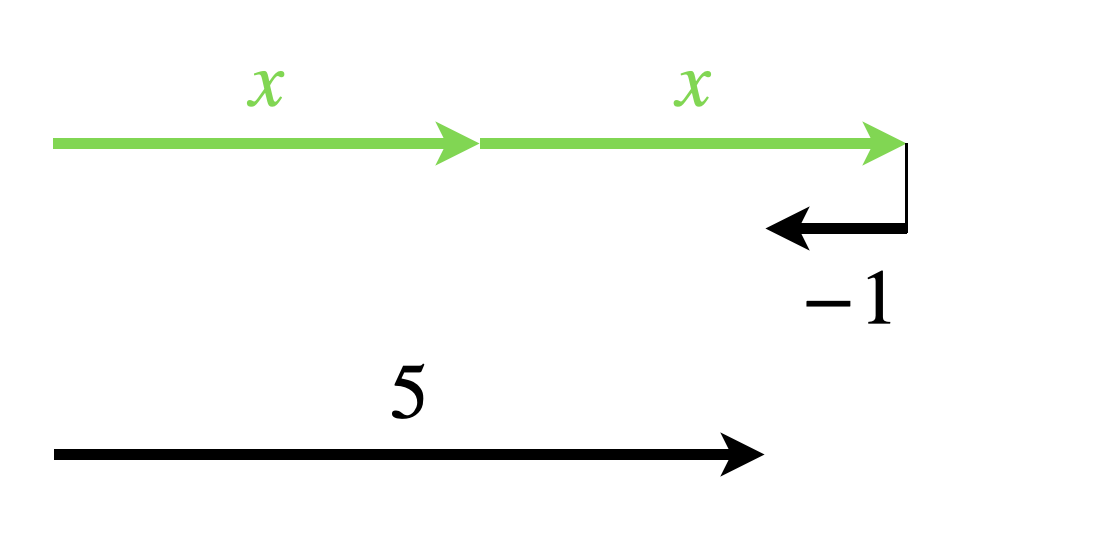
Pfeil-Modell für die Gleichung $2x-1 = 5$

Abb. 5.7: Pfeil-Modell für die Gleichung \(2x-1 = 5\)

  • Das Modell bietet weiterhin die Möglichkeit, die Gleichheit der beiden Terme abhängig vom Wert für \(x\) nachvollziehbar zu machen. Je nachdem, wie groß \(x\) ist, kann also die Gleichung \(2x+1 = 7\) wahr sein (beide Strecken gleich lang) oder eben nicht. Unterstützt werden kann dies, indem \(x\) dynamisch variiert wird, etwa in einem digitalen Arbeitsmittel.
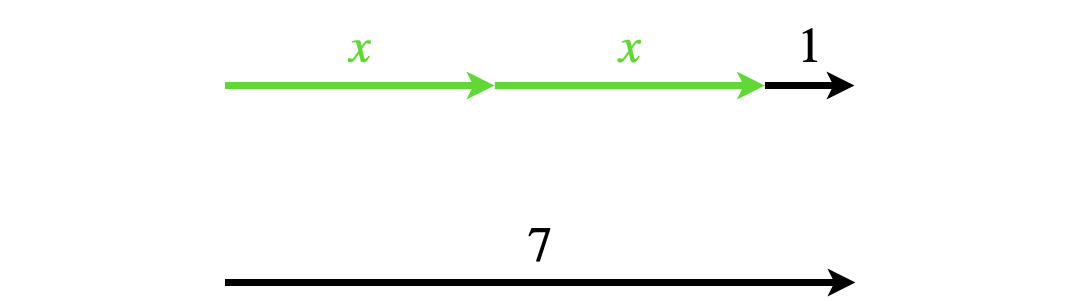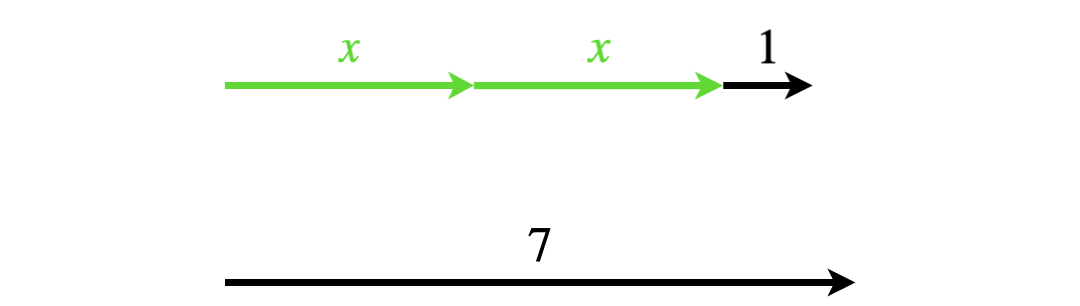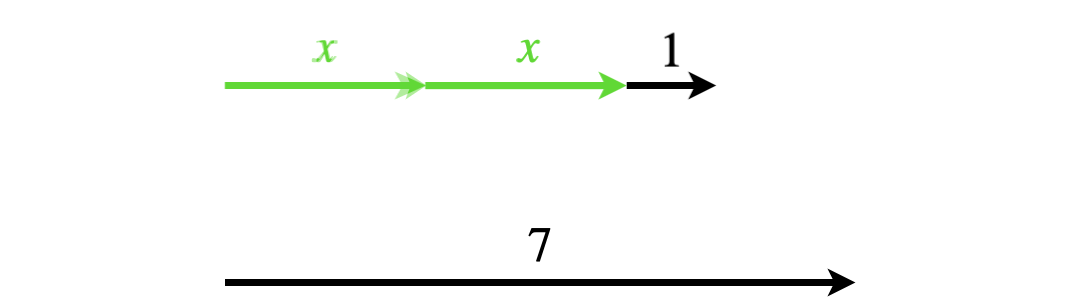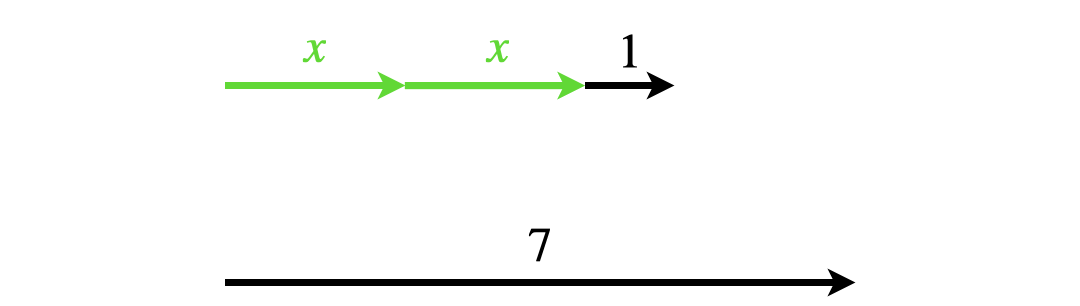
Gleichheit/Ungleichheit der Terme $2x+1$ und $7$ im Pfeil-Modell

Abb. 5.8: Gleichheit/Ungleichheit der Terme \(2x+1\) und \(7\) im Pfeil-Modell

Insofern erfüllt eine Umsetzung dieses Modells über ein digitales Arbeitsmittel, in dem virtuell-enaktiv operiert werden kann, die Forderungen aus Definition 5.1.

5.4 Zum Nachbereiten

In Kapitel 4 sollten Sie sich in der Nachbereitung mit Grundvorstellungen zu Variablen oder Termen beschäftigen.

  1. Recherchieren Sie in Schulbüchern und fachdidaktischer Literatur, welche Materialien üblicherweise zur Unterstützung des Aufbaus entsprechender Grundvorstellungen verwendet werden.

  2. Analysieren Sie eines dieser Materialien hinsichtlich der Eignung als Arbeitsmittel nach Definition 5.1.

References

Barzel, B., & Holzäpfel, L. (2011). Gleichungen verstehen. mathematik lehren, 169, 2–7.
Giest, H., & Lompscher, J. (2006). Lerntätigkeit – Lernen aus kultur-historischer Perspektive. Ein Beitrag zur Entwicklung einer neuen Lernkultur im Unterricht. Lehmanns Media.
Kortenkamp, U., Etzold, H., Goral, J., Schmidt, A., & Börrnert, M. (2018). Digitale Stellenwerttafel – Leitfaden für Lehrerinnen und Lehrer (Version 5). Zenodo. https://doi.org/10.5281/zenodo.4761419
Krauthausen, G. (2018). Einführung in die Mathematikdidaktik (F. Padberg & A. Büchter, Hrsg.; Mathematik Primarstufe und Sekundarstufe I + II). Springer Spektrum. https://doi.org/10.1007/978-3-662-54692-5
Lompscher, J. (1983). Die Ausbildung von Lernhandlungen. In J. Lompscher (Hrsg.), Persönlichkeitsentwicklung in der Lerntätigkeit (S. 53–78). Volk und Wissen.
Lompscher, J. (1996). Aufsteigen vom Abstrakten zum Konkreten - Lernen und Lehren in Zonen der nächsten Entwicklung. https://publishup.uni-potsdam.de/opus4-ubp/frontdoor/deliver/index/docId/444/file/AUFSTEIG.pdf
Reinhold, F., Walter, D., & Weigand, H.-G. (2023). Digitale Medien. In R. Bruder, A. Büchter, H. Gasteiger, B. Schmidt-Thieme, & H.-G. Weigand (Hrsg.), Handbuch der Mathematikdidaktik (S. 523–559). Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-66604-3_17
Wartha, S., & Schulz, A. (2011). Aufbau von Grundvorstellungen (nicht nur) bei besonderen Schwierigkeiten im Rechnen. IPN Kiel. http://www.sinus-an-grundschulen.de/fileadmin/uploads/Material_aus_SGS/Handreichung_WarthaSchulz.pdf
Weigand, H.-G., Schüler-Meyer, A., & Pinkernell, G. (2022). Didaktik der Algebra: nach der Vorlage von Hans-Joachim Vollrath. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-64660-1
Wygotski, L. (1985). Die instrumentelle Methode in der Psychologie. In J. Lompscher (Hrsg.), Lew Wygotski. Ausgewählte Schriften. Teil 1: Arbeiten zu theoretischen und methodologischen Problemen der Psychologie (S. 309–317). Volk und Wissen.

  1. Den Arbeitsmitteln werden hier Anschauungsmittel entgegengestellt, jedoch in einer eher demonstrierenden Bedeutung (Reinhold et al., 2023, S. 526), was eher dem Begriff der Veranschaulichungsmittel bei Krauthausen (2018, S. 310) entspricht.↩︎

  2. Damit sind auch Abbildungen, Strukturdiagramme oder Apps eingeschlossen.↩︎

  3. Dies folgt aus folgender Überlegung:Sei eine Gleichung \(T_1(x) = T_2(x)\) mit der Grundmenge \(\mathbb{G}\) gegeben, \(\mathbb{L}\) die Lösungsmenge der Gleichung und \(\varphi: \mathbb{G}\rightarrow \mathbb{G}\) eine injektive Funktion. Für \(x \in \mathbb{L}\) ist \(T_1(x) = T_2(x)\) eine wahre Aussage und damit \(\varphi(T_1(x)) = \varphi(T_2(x))\), also \(x\in\mathbb{L}_\varphi\), d. h. Lösung der umgeformten Gleichung. Sei weiterhin \(y\in \mathbb{L}_\varphi\), d. h. \(\varphi(T_1(y)) = \varphi(T_2(y))\). Dann ist wegen der Injektivität \(\varphi^{-1}(\varphi(T_1(y))) = \varphi^{-1}(\varphi(T_2(y)))\), also \(T_1(y) = T_2(y)\), also \(y\in\mathbb{L}\). Daraus folgt \(\mathbb{L} = \mathbb{L}_\varphi\).↩︎