12 Analysis
Ziele
- Sie sind sich bewusst, dass Analysis in Universität und Schule unterschiedlich strukturiert sind und dies in der Schulrealität in einen propädeutischen Grenzwertbegriff mündet.
- Sie kennen Grundvorstellungen zum Ableitungsbegriff.
- Sie haben einen Einblick in das Unterrichten mit CAS als Werkzeug für die Schülerinnen und Schüler.
Material
Literaturempfehlungen
12.1 Analysis in der Sek. II
Der Analysisunterricht in der Schule unterscheidet sich wesentlich von dem in der Hochschule, womit aus fachlicher wie fachdidaktischer Sicht einige Herausforderungen einhergehen. Neben der grundsätzlichen nicht streng deduktiven Herangehensweise werden i. d. R. zentrale Begriffe der Analysis im Schulunterricht kaum oder nur propädeutisch-anschaulich behandelt. Die betrifft zunächst einmal den Folgen-, Grenzwert- und Stetigkeitsbegriff (Danckwerts & Vogel, 2010, 17 ff.; Greefrath et al., 2016, 23 ff.; Tietze et al., 2000a, 252 ff.). Der Ableitungsbegriff bedarf bspw. des Grenzwertes des Differenzenquotienten. Ein solcher Grenzwert einer Funktion \(f\) an einer Stelle \(a\) existiert, wenn für alle Folgen \((x_n)_{n\in\mathbb{N}}\) mit \(x_n\rightarrow a\) auch die Folge der Funktionswerte konvergiert, also \(f(x_n)\rightarrow f(a)\). Für den Konvergenzbegriff einer Folge ist nun zum anderen die Vollständigkeit der reellen Zahlen von enormer Bedeutung, was ebenfalls in der Schule nicht in einer derartigen Strenge behandelt wird (siehe z. B. Danckwerts & Vogel, 2010, 27 ff.). Mathematisch relevant ist für die Konvergenz einer Folge \((x_n)_{n\in\mathbb{N}}\) gegen \(a\) eben nicht nur, dass die Folgeglieder dem \(a\) beliebig nahe kommen, sondern dass \(a\) im betrachteten Zahlbereich tatsächlich existiert. Ein klassisches Beispiel hierfür ist das Heron-Verfahren zum Wurzelbestimmen (vgl. Abschnitt 11.2.3). So liefert die rekursive Folge\(x_{n+1} = \frac{1}{2}\left(x_n + \frac{5}{x_n}\right)\) mit bspw. \(x_0 = 1\) ausschließlich Folgeglieder aus \(\mathbb{Q}\), die sich auch beliebig nahe kommen (eine sogenannte Cauchy-Folge), der Grenzwert selbst ist aber \(\sqrt{5}\), was nicht in \(\mathbb{Q}\), sondern nur in \(\mathbb{R}\) liegt.
Ohne derartige zentrale (im fachmathematischen Sinne sauber ausgeprägte) Begriffe Analysisunterricht zu betreiben, bedarf also einer starken Orientierung an den hinter den Begriffen liegenden Grundvorstellungen, damit dennoch ein inhaltlich-anschauliches Verständnis aufgebaut werden kann und der Unterricht nicht zu einem kalkülhaften Vorgehen verkommt. Spezifische Anregungen für einzelne Lerngegenstände bieten die bereits zitierten Quellen.
12.2 Grenzwertbegriff
12.2.1 Fachliche Hinweise
Da in der Schule i. d. R. keine systematische Behandlung von Folgen erfolgt, ist auch eine formale Definition des Grenzwertbegriffes nicht möglich. Man bedient sich daher – und so wird es auch im Brandenburgischen Rahmenlehrplan verlangt – eines propädeutischen Zugangs zum Grenzwertbegriff (vgl. Ministerium für Bildung, Jugend und Sport des Landes Brandenburg, 2022b, 25, 28). Damit ist gemeint, dass der Begriff vorgebildet wird, ohne auf eine formale Definition zurückzugreifen. Diese Propädeutik kann dann entweder dazu dienen, später formalisiert zu werden (was beim Grenzwertbegriff jedoch in der Schule normalerweise nicht geschieht, sondern dann erst in einem Mathematikstudium erfolgt) oder aufbauend auf die Propädeutik andere Begrifflichkeiten einzuführen (wie den Ableitungsbegriff). Dabei werden zwar fachliche Lücken hingenommen, aber dennoch versucht, ein Begriffsverständnis aufzubauen.
Formal kann der Grenzwert bzw. die Konvergenz einer Folge definiert werden:
Eine Folge \(a_n\) heißt konvergent gegen den Grenzwert \(a\), wenn für jedes \(\varepsilon > 0\) ein \(n_0\) existiert, so dass für alle \(n>n_0\) gilt: \(|a_n-a| < \varepsilon\).
Dabei muss noch festgelegt werden, aus welchem (gemeinsamen) Zahlbereich \(a\) und die \(a_n\) stammen. Die in Abbildung 12.1 dargestellte Visualisierung zum Grenzwertbegriff steht auch als virtuelles Arbeitsmittel über https://www.geogebra.org/m/fwzbx3xa zur Verfügung.
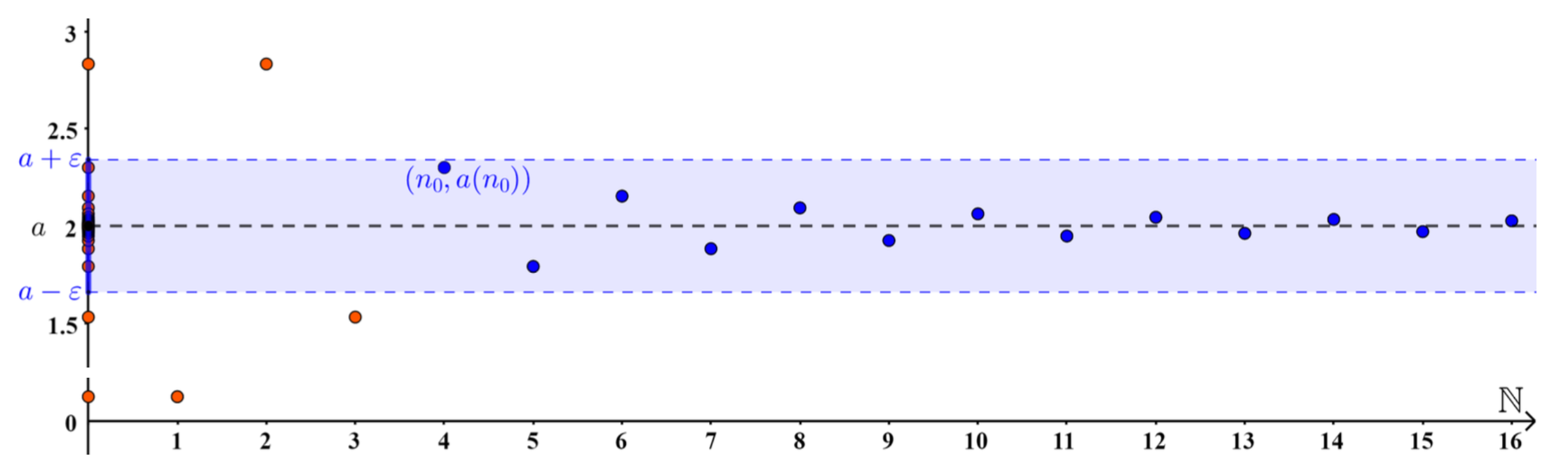
Abb. 12.1: Visualisierung zum Grenzwertbegriff (Enders, 2024, S. 36)
Aus der formalen Definition ergeben sich einige Schlussfolgerungen, die – bei fehlender formaler Definition und einem rein intuitiven Zugang – häufig mit fehlerhaften Vorstellungen zur Konvergenz und zum Grenzwert einhergehen. Formuliert werden im Folgenden die mathematisch korrekten Aussagen.
Es ist notwendig, dass der Grenzwert \(a\) tatsächlich im betrachteten Zahlbereich auch existiert – ansonsten kann nicht von Konvergenz gesprochen werden. Es reicht also nicht aus, dass die Folgeglieder einander immer näher kommen.35 Ein typisches Gegenbeispiel hierfür ist die rekursive Folge \(a_{n+1} = \frac{1}{2}\left(a_n+\frac{5}{a_n}\right)\), \(a_0 = 1\), die das Heron-Verfahren beschreibt (siehe Abschnitt 11.2.3). Betrachtet man diese Folge in \(\mathbb{Q}\) (wobei wegen der Grundrechenarten alle Folgeglieder in \(\mathbb{Q}\) bleiben), so ist diese dort nicht konvergent, weil es in \(\mathbb{Q}\) keine Zahl gibt, der die Folgeglieder beliebig nah kommen. Erst in \(\mathbb{R}\) ist diese Folge konvergent gegen den Grenzwert \(\sqrt{5}\).36
Die Reihenfolge der Folgeglieder ist irrelevant für die Konvergenz. Da bei einer konvergenten Folge fast alle Folgeglieder (also alle bis auf endlich viele) in der \(\varepsilon\)-Umgebung des Grenzwertes liegen, kann bei einer umsortierten Folge das letzte Folgeglied gesucht werden, welches geradeso nicht mehr in der \(\varepsilon\)-Umgebung liegt und anschließend ab dessen Nachfolger das Konvergenzkriterium erfüllt werden.
Die Folgeglieder können zwar, aber müssen dem Grenzwert nicht bei jedem Schritt immer näher kommen. Bei der Folge \[0,33\quad 0,3\quad 0,3333 \quad 0,333 \quad0,333333 \quad \ldots\] kommt bspw. nur jedes zweite Folgeglied dem Grenzwert \(\frac{1}{3}\) näher, dennoch konvergiert die Folge, weil bei vorgegebener Genauigkeit (\(\varepsilon\)) ein Folgeglied gefunden werden kann (\(a_{n_0}\)), ab dem alle diese Genauigkeit erfüllen (vgl. Ableitinger & Heitzer, 2013, S. 7).
Es ist irrelevant, ob der Grenzwert erreicht wird oder nicht. Bei den meisten Beispielen kommen die Folgeglieder dem Grenzwert immer näher, ohne ihn jemals zu erreichen. Dies ist jedoch für die Konvergenz nicht relevant. Es ist durchaus möglich, dass der Grenzwert ab einem bestimmten \(n_0\) tatsächlich erreicht wird (oder auch zwischendurch immer mal wieder). Insofern sind auch konstante Folgen konvergente Folgen.
12.2.2 Unterrichtliche Zugänge
Um trotz eines nur propädeutischen Zugangs zum Grenzwertbegriff Schul-Analysis betreiben zu können, bedarf es (auch schon in der Sekundarstufe I) vielfältiger Erfahrungen zu Grenzprozessen, bei denen die hinter dem Grenzwertbegriff stehenden Ideen sichtbar werden. Greefrath et al. (2016, 107 ff.) und Ableitinger & Heitzer (2013, S. 3) führen hierzu vielfältige Vorschläge auf, aus denen hier einige vorgestellt werden sollen.
- In geometrischen Situationen können Grenzprozesse betrachtet werden, etwas bei der näherungsweisen Bestimmung des Flächeninhalts eines Kreises über das Ein- und Umschreiben mittels regelmäßiger \(n\)-Ecke.

Abb. 12.2: Näherungsweise Bestimmung des Kreisflächeninhalts
In numerischen Situationen kann die Idee des Grenzprozesses verdeutlicht werden, etwa wenn die Zahl \(\frac{1}{3}\) notiert wird als \(\frac{1}{3} = 0,\bar{3} = 0,3 + 0,03 + 0,003 + \ldots\) oder die Gleichheit von \(0,\bar{9} = 1\) diskutiert wird. Auch die Durchführung einer Intervallschachtelung (siehe Abschnitt 11.2.2) fördert das Verständnis für Grenzprozesse. Auch zu Beginn der Sekundarstufe können Erfahrungen gesammelt werden, z. B. über eine Partneraufgabe, bei der eine Person eine (positive) Zahl nennen muss und die zweite Personen einen Stammbruch (also einen Bruch der Form \(\frac{1}{n}\)) finden muss, der kleiner als die genannte Zahl ist.
In der Kombination geometrischer und numerischer Situationen liegt ebenfalls Potenzial für die Erfahrung von Grenzprozessen. Die geometrische Interpretation des Heron-Verfahrens (vgl. Abbildung 11.3) wäre ein Beispiel hierfür. Auch kann die Summation \(2 = 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8}+\ldots\) erfahren werden, in dem ein Papierstreifen der Länge \(2\) fortlaufend halbiert wird.
12.3 Ableitungsbegriff
Für den Ableitungsbegriff (einer Funktion an einer Stelle) haben sich sowohl historisch als auch in der fachdidaktischen Literatur zwei wesentliche Vorstellungen herausgebildet (Danckwerts & Vogel, 2010, 45 ff.; Greefrath et al., 2016, 147 ff.)37:
Ableitung als lokale Änderungsrate: Die Ableitung einer Funktion an einer Stelle beschreibt, wie stark sich die Funktionswerte in der Umgebung dieser Stelle verändern. Wird sich dieser Änderungsrate graphisch genähert, erfolgt dies i. d. R. durch den Übergang des Anstiegs einer Sekante zu dem einer Tangente38, womit die Ableitung über den Grenzwert des Differenzenquotienten \(\lim\limits_{h\rightarrow 0}\cfrac{f(x_0+h)-f(x_0)}{h}\) quantifiziert werden kann und dem Anstieg der Tangente entspricht.
Diese Sichtweise ermöglicht, den Ableitungbegriff konstruktiv über den Sekanten-Tangenten-Übergang einzuführen und unmittelbar numerisch zu beschreiben. Auch bedienen sich vielfältige Anwendungen (z. B. Momentan- vs. Durchschnittsgeschwindigkeit) dieser Vorstellung.
Ableitung als lokale lineare Approximation: Diese Vorstellung betont noch stärker die Differenzierbarkeit als Eigenschaft einer Funktion, nämlich die Möglichkeit, sie lokal durch eine lineare Funktion annähern zu können. Eine typische Repräsentation ist das Heranzoomen an den Funktionsgraphen, sodass dabei die lokale Linearität besonders deutlich wird. Mathematisch greifbar wird diese Vorstellung darüber, dass sich die Funktion über \(f(x) = f(x_0) + m\cdot x+ r(h)\) beschreiben lässt, wobei der Fehler \(r(h)\) so schnell gegen \(0\) geht, dass sogar \(\lim\limits_{h\rightarrow 0}\cfrac{r(h)}{h}=0\) gilt. \(m\) selbst ist dann die Ableitung und der Anstieg der besten linearen Näherung – was natürlich wieder die Tangente an entsprechender Stelle ist.
Dieses Vorgehen besticht v. a. durch seine mathematische Verallgemeinerbarkeit für die höherdimensionale Analysis. Auch entspricht es dem Bedürfnis, Prozesse linear zu approximieren (vgl. Abschnitt 3.4.3).
12.4 Computer-Algebra-Systeme
Insbesondere – aber nicht ausschließlich – im Analysis-Unterricht spielt die Verwendung von Computer-Algebra-System (CAS) eine bedeutsame Rolle. In ihrer eigentlich Bezeichnung ist ein CAS ein digitales Werkzeug, das symbolische Rechnungen erlaubt, also bspw. für die Gleichung \(x^2 = 5\) die Lösungen \(\sqrt{5}\) und \(-\sqrt{5}\) ausgeben kann, während ein numerisch rechnendes System hier bspw. \(2,23607\) ausgeben (und die zweite Lösung womöglich sogar unterschlagen) würde.39
Insbesondere im schulischen Alltag hat sich »CAS« mittlerweile zum Gattungsbegriff für vielfältige Arten von Taschenrechnern und anderen digitalen Werkzeugen gewandelt. Darunter werden also auch verstanden:
- Wissenschaftliche Taschenrechner (WTR), also Taschenrechner, die wesentliche mathematische Funktionen enthalten (z. B. auch die Berechnung von Potenzen, dem Sinus usw.) und Punkt- vor Strichrechnung beherrschen.
- Graphikfähige Taschenrechner (GTR), die neben der Funktionalität wissenschaftlicher Taschenrechner auch Funktionsgraphen darstellen können und diese numerisch untersuchen können (z. B. Schnittpunktbestimmung). Sowohl beim GTR als auch bei CAS handelt es sich in der Regel um programmierbare Taschenrechner, d. h. es können selbst Algorithmen implementiert werden, die dann als Funktion zur Verfügung stehen.
- Tabellenkalkulationen (TK), in denen mit strukturiert notierten Daten gerechnet werden kann.
- Dynamische Geometriesysteme (DGS), die die Möglichkeit bieten, geometrische Konstruktionen darzustellen. Mehr dazu finden Sie in Abschnitt 13.2.
12.4.1 Software und Hardware
Am weitesten sind an Schulen derzeit noch »echte« Taschenrechner mit CAS-Funktionalität verbreitet, i. d. R. von den Firmen Casio, TI, HP oder Sharp. Einige Bundesländer formulieren Voraussetzungen, über welche Funktionalitäten derartige Systeme verfügen müssen (und nicht verfügen dürfen), so dass sie auch in Prüfungssituationen verwendet werden können.
Stärkere Verbreitung finden mittlerweile Software-Lösungen, die spezifisch für schulische Zwecke entwickelt worden sind, z. B. die CAS-Funktion von GeoGebra40. Auch Apps wie Photomath41 können als CAS aufgefasst werden. In Schulen i. d. R. nicht verbreitet sind professionelle kommerzielle Angebote wie Maple oder Matheamtica. Es gibt jedoch auch freie CAS-Software, die zwar nicht explizit für schulische Zwecke entwickelt worden ist, aber dennoch für Schülerinnen und Schüler zugänglich ist und (aus fachmathematischer Sicht) »echte« CAS-Lösungen darstellt. Hierzu gehören etwa Yacas42 oder Sage43, die wie GeoGebra über Online-Editoren verfügen.
12.4.2 Bedienung schulen
Das Lernen der Bedienung eines CAS erfolgt nicht »nebenbei« zum Lernen der mathematischen Zusammenhänge, sondern muss explizter Lerngegenstand werden. Hierzu ist es notwendig, die entsprechenden CAS-Befehle mit den dahinter liegenden mathematischen Handlungsfolgen in Bezug zu bringen, bspw. über eine Versprachlichung des Befehls und seiner Bestandteile.

Abb. 12.3: CAS-Befehl zum Lösen einer Gleichung
Für den in Abbildung 12.3 dargestellten Befehl kann als Erläuterung dienen: »Der Befehl löst die Gleichung \(x^2 = 5\), d. h. es werden diejenigen Werte für \(x\) gesucht, für die die Gleichung eine wahre Aussage ergibt.«
Derartige Bedienschulungen können dann wieder durch Identifizierungs- und Realisierungs- sowie Festigungsaufgaben angeeignet werden, das heißt u. a.:
- Zu vorgegebenen Beschreibungen müssen entsprechende Befehle ins CAS eingegeben werden.
- Zu gegebenen Befehle soll beschrieben werden, wofür diese dienlich sind.
- Befehle oder die in ihnen enthaltenen Bestandteile müssen variiert werden und die Einflüsse der Variation untersucht bzw. beschrieben werden.
Weiterhin ist es notwendig, die hinter dem Befehl liegende Mathematik nachvollziehen zu können. Es reicht also nicht aus, das CAS als Black-Box aufzufassen, dass aus der Eingabe solve(x^2=5,x) irgendwie die Ausgabe √5,-√5 erzeugt, sondern es sollten stets die dahinterliegenden Prozesse hinterfragt werden. Dies kann auch über die Darstellung von (Pseudo-)Algorithmen erfolgen, wobei nicht jeder Schritt (oder nicht einmal der komplette Algorithmus) der tatsächlichen algorithmische Umsetzung im Hintergrund des CAS entsprechen muss, solange er mathematisch nachvollziehbar ist. Im genannten Beispiel könnte ein solcher Pseudoalgorithmus, der nach der Eingabe des Befehls solve(x^2=5,x) abläuft, lauten:
- Prüfe, ob es sich um eine quadratische Gleichung handelt.
- Bringe die Gleichung in die Form \(0 = x^2+px+q\).
- Bestimmte \(p\) und \(q\).
- Gibt die Lösungen \(-\frac{p}{2}+\sqrt{\left(\frac{p}{2}\right)^2-q}\) und \(-\frac{p}{2}-\sqrt{\left(\frac{p}{2}\right)^2-q}\) aus.
12.4.3 Neue Aufgabenkultur
In der Verwendung von CAS ergibt sich die Notwendigkeit einer neuen Aufgabenkultur, da eine klassische Aufgabe der Art »Ermittle die Lösungsmenge der Gleichung \(x^2 = 5\)« mithilfe eines CAS, sofern der entsprechende Befehl bekannt ist, keine mathematisch-gedankliche Herausforderung mehr darstellt.
Kortenkamp (2007) schlägt beispielsweise vor, das CAS als Überprüfungsinstrument zu verwenden, um selbst erzeugte Aufgaben zu prüfen. Im oben genannten Beispiel könnte eine Aufgabenstellung lauten: »Stell eine quadratische Gleichung auf, die \(\sqrt{5}\) als Lösung hat.« Solche Aufgaben können dann schrittweise variiert und komplexer gestaltet werden (»Stell eine quadratische Gleichung auf, die nur \(\sqrt{5}\) als Lösung hat« usw.).
Die von einem CAS ausgegebene Lösung kann wiederum als Anlass genutzt werden, mathematische Fragen zu stellen. Im obigen Beispiel wäre möglich zu fragen: »Warum gibt das CAS zwei Lösungen aus?«, »Wie hängen die Lösungen miteinander zusammen?« o. ä. Derartige Fragen sollten auf die hinter der Aufgabe liegende Struktur hinzielen.
Nicht zu verschweigen ist auch, dass sich durch die Verwendung von CAS (und anderen Taschenrechnern) sogenannte »oHiMi«-Aufgaben etabliert haben, also Aufgaben, die ohne Hilfsmittel zu bearbeiten sind. Dahinter steckt die Auffassung, dass Schülerinnen und Schüler über gewisse Basiskenntnisse und -fertigkeiten verfügen sollten, die dann auch in Prüfungssituationen abgefragt werden. Entsprechende Erwartungen sind in den Lehrplänen formuliert, in Brandenburg z. B. über eine Anlage zum Rahmenlehrplan der gymnasialen Oberstufe (Ministerium für Bildung, Jugend und Sport des Landes Brandenburg, 2022a).
Eine etwas ausführlichere – und auch über 15 Jahre nach ihrer Entstehung immer noch nicht vollumfänglich im Schulalltag angekommene – Diskussion zum Einfluss von CAS und Graphikfähigen Taschenrechnern auf die Aufgabenkultur findet sich bei Heinrich (2007).
References
Hierfür existiert der Begriff der Cauchy-Folge.↩︎
Daher kann die Konvergenz von Cauchy-Folgen auch als Charakteristikum von \(\mathbb{R}\) genutzt werden.↩︎
Greefrath et al. (2016, 147 ff.) trennen die lokale Änderungsrate noch von der Vorstellung des Anstiegs der Tangente und beschreiben als vierte Grundvorstellung die Ableitung als Verstärkungsfaktor kleiner Änderungen.↩︎
Zur Diskussion der Vorstellung, was eine Tangente ist, siehe auch Greefrath et al. (2016, S. 149)↩︎
Streng genommen ist dieses Beispiel hier im Kapitel falsch, da es eher ein algebraisches Problem ist. Es soll aber dennoch weiter verfolgt werden.↩︎