7 Intermezzo: Flächeninhalt
Ziele
- Sie vertiefen Ihr Verständnis über den Vier-Ebenen-Ansatz.
- Sie verknüpfen Ihre Kenntnisse über fundamentale Ideen, Grundvorstellungen, Kontexte und Kernideen/Kernfragen am Beispiel des Flächeninhaltsbegriffs.
Material
In diesem Kapitel werden fundamentale Ideen, Grundvorstellungen, Kernideen/Kernfragen und Kontexte im Zusammenhang mit dem Flächeninhaltsbegriff diskutiert. Ein Schulbuchkapitel zum Flächeninhaltsbegriff bietet die Motivation, die formale, semantische und konkrete Ebene des Vier-Ebenen-Ansatzes zu diskutieren und einen ersten Ausblick auf die empirische Ebene zu geben.
In dem Sinne wird also existierendes Material analysiert und hinsichtlich der mathematikdidaktischen Theorie reflektiert. Ein solches Vorgehen wäre auch für Ihren Seminarvortrag bzw. die Hausarbeit im Rahmen dieser Veranstaltung möglich – dann natürlich etwas ausführlicher, als hier dargestellt.
7.1 Darstellung im Schulbuch
In dem Schulbuch Mathewerkstatt (Barzel et al., 2012c) wird der Flächeninhalt über den Kontext von Tiergehegen eingeführt (siehe Abbildung 7.1). So haben in einem Zoo verschiedene Tiere unterschiedlich große Gehe zur Verfügung. Die Form der Gehege variiert dabei ebenfalls.

Abb. 7.1: Einstiegsbild zum Thema Flächeninhalt (Barzel et al., 2012c, 168 f.)
Die Schülerinnen und Schüler werden nun in einer Erkundungsphase vor die Aufgabe gestellt, die Gehegegrößen miteinander zu vergleichen sowie möglichst geschickt die Größe eines Geheges messen zu können.
Anschließend erfolgen Ordnungs- und Vertiefungsphasen, in denen das Wissen struktruiert und geübt wird. Das Schulbuch wird durch einen Materialblock begleitet (Barzel et al., 2012b), was in diesem Fall insbesondere dem Auseinanderschneiden und Zusammenlegen bzw. dem Auslegen von Flächen dienen soll. Weiterhin gibt es für Lehrerinnen und Lehrer ein ausführliches Begleitmaterial (Barzel et al., 2012a), in dem alle Seiten des Schulbuches sowie fachdidaktische Hintergründe zur Thematik erläutert sind.
7.2 Formale Ebene
Welche Begriffe, Sachverhalte und Verfahren sollen erarbeitet werden?
Wie können die Sachverhalte und Verfahren formal begründet werden?
Wie kann das Netzwerk aus Begriffen, Sachverhalten und Verfahren logisch strukturiert werden?
Welche Verbindungen zwischen den Fachinhalten sind aus fachlicher Perspektive entscheidend, welche weniger?
Fachmathematisch kann der Flächeninhalt einer Figur als ein nichtnegatives Maß aufgefasst werden, wobei zwei zueinander kongruenten Figuren dasselbe Maß zugeordnet wird und der Flächeninhalt einer Figur gleich der Summe der Flächeninhalte ihrer Teilfiguren ist, sofern zerlegbar. Hinzu wird das Flächeninhaltsmaß eines Quadrates der Seitenlänge 1 LE auf 1 LE2 festgelegt (vgl. Kuntze, 2018, S. 161).
Dies ist eine axiomatische Herangehensweise, die sich für Schülerinnen und Schüler in der Regel als herausfordernd darstellt (Kuntze, 2018, S. 162). Häufig wird eine umschreibende Definition genutzt, wie: Der Flächeninhalt einer Fläche gibt an, wie groß diese ist. Dabei ist jedoch die mögliche Mehrdeutigkeit dieser Formulierung zu beachten – so könnte auch der Umfang einer Figur als Maß für ihre Größe aufgefasst werden, da der Größenbegriff in dem Fall unspezifisch ist.
Ob nun eine explizite Definition gewählt wird oder nicht – dies ist auch abhängig von der persönlichen Einstellung der Lehrkraft und den Voraussetzungen der Lerngruppe – in jedem Fall ist ein tragfähiges mathematisches Verständnis aufzubauen. Hierzu können die in den Axiomen enthaltenen Eigenschaften über sinnvolle Lernhandlungen aufgebaut werden (siehe auch Wörner, 2014, 1328 f.):
- Vergleichen verschiedener Flächen durch Zerlegen, Ergänzen und Übereinanderlegen
- Bestimmen des Maßes einer Fläche über Auszählen mittels eines Vergleichsmaßes
- Nutzen eines quadratischen Vergleichsmaßes, in der Regel 1 cm2
All diese Überlegungen kommen zunächst ohne Formeln aus, weshalb Formeln im Unterricht auch erst im Anschluss an eine inhaltliche Erarbeitung des Flächeninhaltsbegriffs eingeführt und genutzt werden sollten.
Fachsystematisch entscheidend ist, dass ein Flächenvergleich zunächst ohne ein explizites Maß möglich ist – hierfür reichen die Kongruenzeigenschaft und das Zerlegen/Ergänzen von Flächen aus. Das Vergleichsmaß ist dann relevant, wenn man den Flächeninhalt mithilfe einer Zahl objektivieren bzw. ohne eine explizite Vergleichsfigur auskommen möchte.
Interessant ist hier auch die Willkürlichkeit des Vergleichsmaßes. Kulturell geprägt ist (in Kontinentaleuropa) zwar beispielsweise 1 cm2, aber auch andere Einheiten sind gleichberechtigt möglich. Auch muss das Vergleichsmaß nicht zwingend ein Quadrat sein. Nicht selten wird z. B. von großen Flächen angegeben, wie viele Fußballfelder in sie hineinpassen würden. Für den Unterricht bedeutet das, dass im Sinne einer auf den mathematischen Kern orientierten Sichtweise zunächst möglichst allgemeine und vielfältige (auch unförmige) Vergleichsflächen herangezogen werden können. Später ist dann natürlich ein Bezug zu den Standardeinheiten herzustellen (siehe Abbildung 7.2).
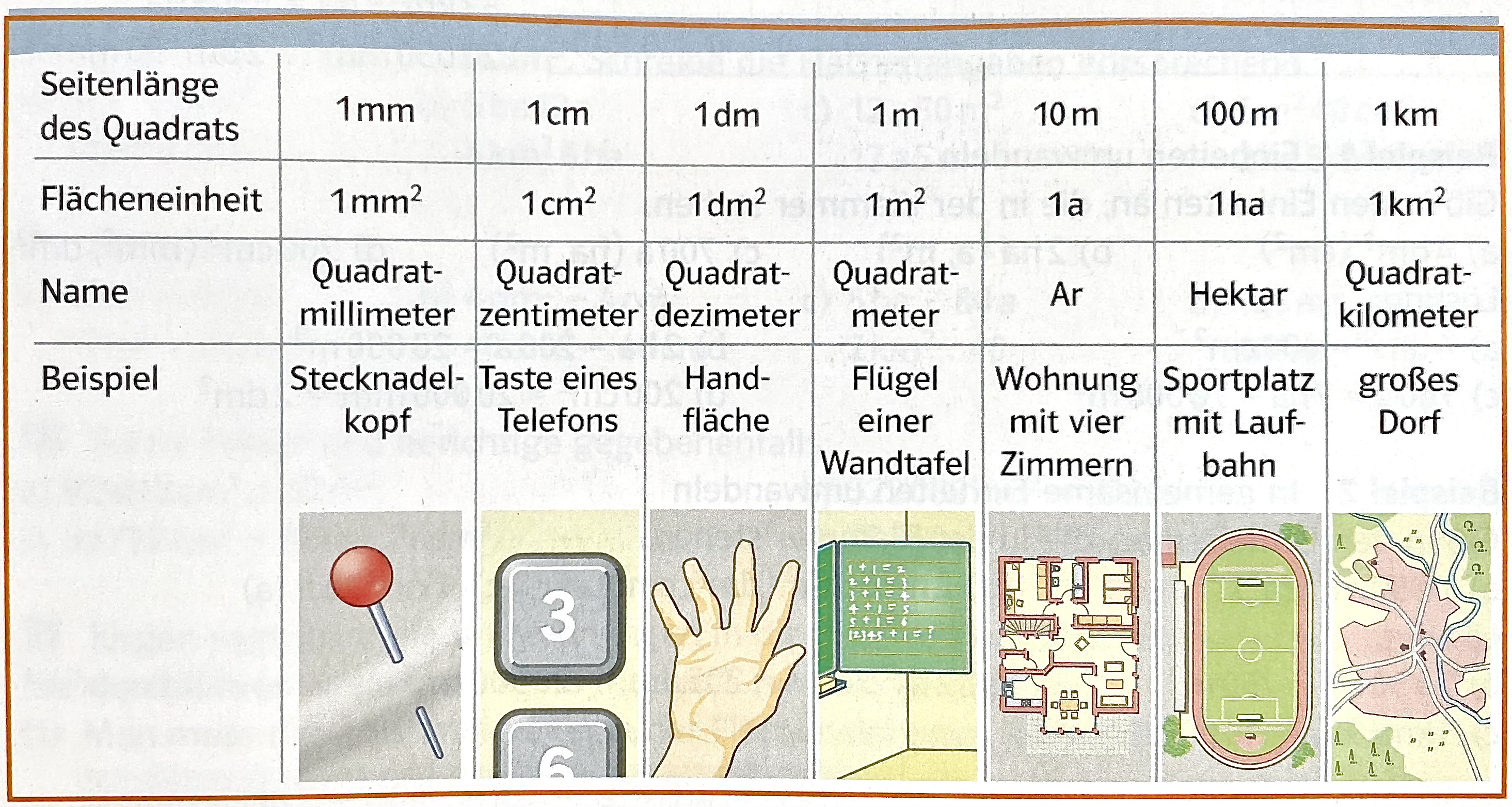
Abb. 7.2: Standardeinheiten typischer Vergleichsflächen (Lambacher Schweizer Mathematik für Gymnasien. 5, Schülerbuch, 2010, S. 193)
7.3 Semantische Ebene
Welche (mathematisch-gesellschaftliche) Bedeutung liegt hinter dem Lerngegenstand (vgl. Fundamentale Ideen?
Welcher Sinn soll bei den Schülerinnen und Schülern hinsichtlich des Lerngegenstands aufgedeckt werden und welche Repräsentationen sind dafür geeignet (vgl. Grundvorstellungen?
Wie verhalten sich Sinn und Bedeutung des Lerngegenstands zueinander und zu früheren und späteren Lerngegenständen?
7.3.1 Fundamentale Idee Messen
Dem Flächeninhaltsbegriff liegt zweifelsohne die fundamentale Idee des Messens zugrunde. Vohns (2000, 52 ff.) stellt ausführlich dar, warum das Messen als fundamentale Idee aufgefasst werden kann, worauf in diesem Abschnitt Bezug genommen wird. Besondere Betonung legt Vohns (2000, S. 49) darauf, dass Messen »der indirekte Vergleich von Objekten in bezug [sic] auf eine bestimmte Eigenschaft« ist.
Horizontal zieht sich dies über viele Gebiete der Mathematik hinweg (z. B. Messprozesse in der Geometrie, Maßzahlaspekt von Brüchen in der Arithmetik, Erwartungswert als Lagemaß in der Stochastik, Integral in der Analysis), aber auch darüber hinaus ist das Messen von hoher Relevanz (z. B. Messprozesse in der Physik, quantitative Studien in den Sozialwissenschaften, Pulsmessung in der Medizin). Damit wird auch das Sinnkriterium der fundamentalen Idee offensichtlich.
Das Vertikalkriterium zeigt sich beispielsweise in der Längenbestimmung in der Grundschule, Flächeninhaltsbestimmung in der Orientierungsstufe, bei Verwandlungen von Flächen (z. B. beim Beweis des Satzes des Pythagoras) bzw. der Approximation von Flächen (z. B. Bestimmen des Kreisflächeninhalts) bis hin zum Integralbegriff als verallgemeinerter Flächeninhalt.
Historisch ist das Messen ebenfalls in vielen Epochen der Mathematik bedeutsam, worauf typische Wortwendungen wie Alles ist Zahl! (bei den Pythagoräern), Die Vermessung der Welt (mit der Methode der Triangulation) oder die Quadratur des Kreises (als klassisches Problem der Geometrie) hindeuten. Auch die Vereinheitlichung von Maßeinheiten (z. B. SI-Einheiten) zeigt die Bedeutsamkeit des Messens für die wissenschaftliche Entwicklung.
7.3.2 GV zum Flächeninhalt
Die folgenden Überlegungen sind empirisch nicht abgesichert, sondern vorwiegend theoretischer Natur. Ansatzpunkt ist ein Beitrag von Wörner (2014). Setzt man die dortigen Darstellungen genauer mit der Definition 4.1 von Grundvorstellungen in Bezug, lassen sich (meiner Meinung nach) Grundvorstellungen zu drei Aspekten des Flächeninhaltsbegriffs formulieren:
- Maßzahlaspekt: Flächeninhalt einer Figur als nichtnegative Maßzahl, die mittels normierter Flächeninhaltsmaße bestimmt wird
- Vereinigungsaspekt: Flächeninhalt einer Figur als Summe der Flächeninhalte der Teilfiguren, aus denen sich die Figur zusammensetzen lässt
- Kongruenzaspekt: Flächeninhalt einer Figur als invariante Eigenschaft gegenüber Kongruenzabbildungen
Für jeden dieser Aspekte sollen nun Handlungserfahrungen, Repräsentationen und mögliche Anwendungen auf die Realität diskutiert werden. Weiterhin werden einige Operationen mit Flächeninhalten besprochen.
7.3.2.1 Maßzahlaspekt
Eine Erfahrung, die die Grundvorstellung zu diesem Aspekt stützt, ist das Auslegen von Flächen mittels normierter Flächenstücke, wie z. B. Quadrate. Hieraus kann die Erfahrung gewonnen werden, dass die Anzahl der Quadrate direkt den Flächeninhalt (mit der entsprechenden Einheit) angibt.
Als Repräsentation kann hierfür einfaches Kästchenpapier dienen, auf das die auszumessende Fläche gemalt wird (siehe Abbildung 7.3). Daran kann man das Abzählen der normierten Flächenstücke durchführen bzw. sich vorstellen. Insbesondere können daran auch Verfeinerungen (und damit genaueres Messen) nachvollzogen werden.
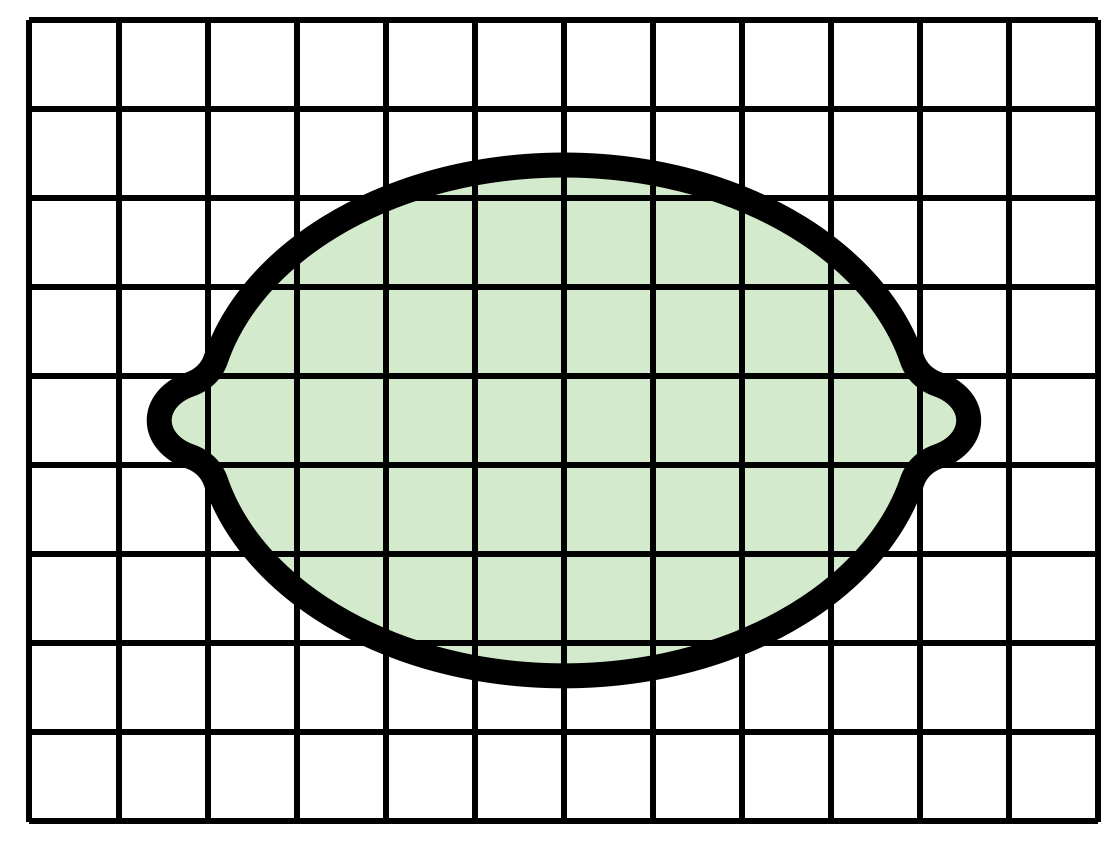
Abb. 7.3: Repräsentation des Maßzahlaspektes
Eine mögliche Anwendung in der Realität ist das Bestimmen der Größe eines Fußballfeldes. Hier kann man die Länge und Breite in Metern messen, um zu bestimmen, wie viele Quadratmeter in das Feld passen. Dies wird dann zwar nicht über tatsächliches Auslegen realisiert, aber es wird (bei Verwendung der Rechteckinhaltsformel) auf die entsprechende Vorstellung Bezug genommen.
7.3.2.2 Vereinigungsaspekt
Zur Grundvorstellung des Vereinigungsaspektes gehört die Erfahrung, Flächen auseinanderzuschneiden und neu zusammenzulegen, um ihren Flächeninhalt bestimmen bzw. die Größe zweier Flächen miteinander vergleichen zu können.
Die Schnittlinien können bspw. durch gestrichelte Linien repräsentiert werden, so dass die Handlungserfahrung hier in der Vorstellung nachvollzogen werden kann (siehe Abbildung 7.4).

Abb. 7.4: Repräsentation des Vereinigungsaspektes
Möchte man die Größe eines Landes bestimmen, so ist es in der Regel notwendig, dieses in geeignete Flächenstücke zu zerlegen, deren Flächeninhalte einfacher berechnet werden können. Dies ist also eine mögliche Anwendung in der Realität. Je nach Komplexität der Figur (und ggf. zusätzlichen geometrischen Überlegungen) können so auch Flächeninhaltsformeln gefunden werden (was schon eine innermathematische Anwendung ist).
7.3.2.3 Kongruenzaspekt
Wer hat größere Hände? Um diese Frage zu beantworten, ist eine typische Erfahrung, die Hände aneinanderzulegen und ihre Größen zu vergleichen. Dabei wird die Vorstellung genutzt, dass zueinander kongruente Figuren den gleichen Flächeninhalt haben.
Eine Repräsentation, die dabei unterstützt, im Kongruenzaspekt zu operieren, kann in der Teilung oder Ummantelung von Figuren mittels zueinander kongruenter Figuren liegen (siehe Abbildung 7.5). Dies ist z. B. bei der Herleitung der Flächeninhaltsformel für ein Dreieck sinnvoll, um zu erkennen, dass dieser der Hälfte des Flächeninhalts des umschriebenen Rechtecks entspricht19.
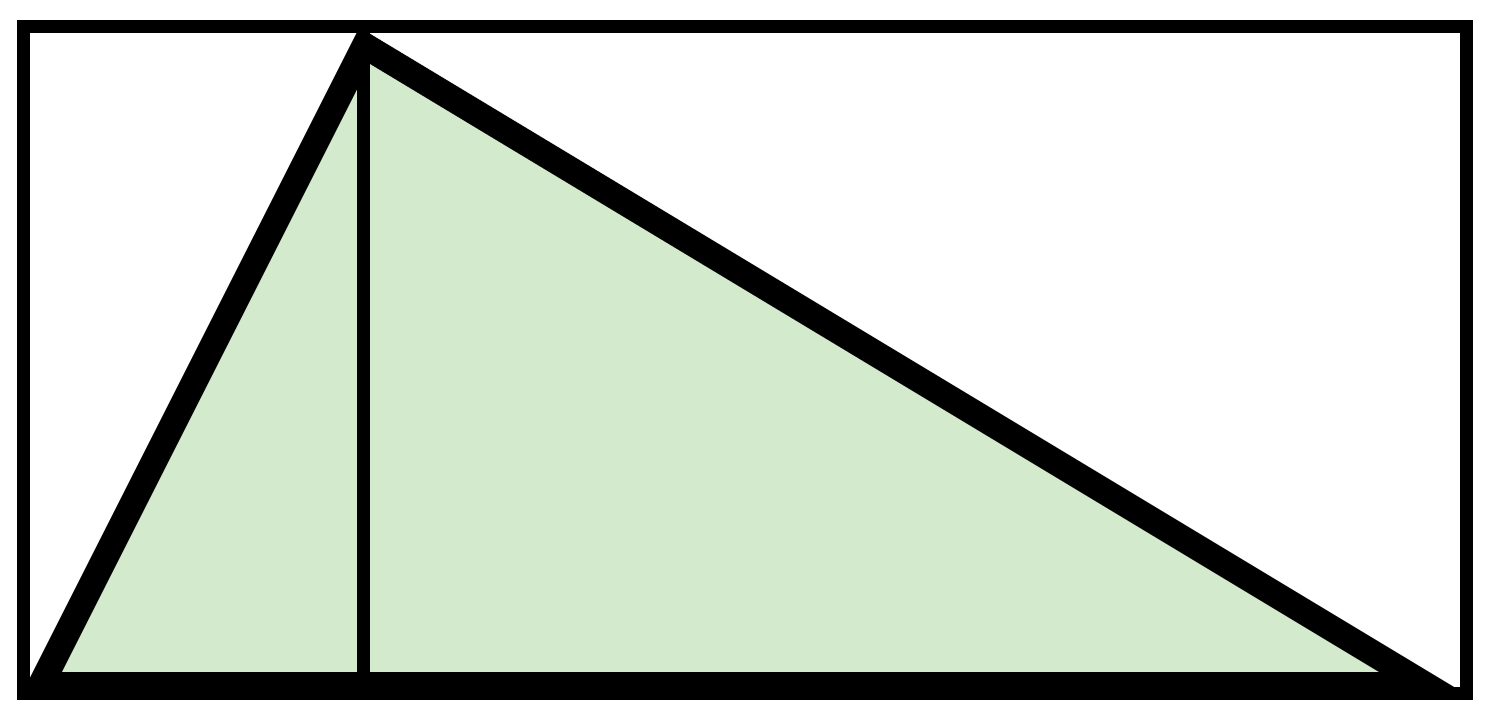
Abb. 7.5: Repräsentation des Kongruenzaspektes
Eine (innermathematische) Anwendung dieser Vorstellung könnte zum Beispiel bei der Berechnung des Oberflächeninhalts eines Primas liegen, wo die Flächeninhalte von Grund- und Deckfläche i. d. R. nicht einzeln berechnet werden, sondern einer der Flächeninhalte wegen der Kongruenz einfach verdoppelt wird.
7.3.2.4 Operieren mit Flächeninhalten
Für unterschiedliche Operationen, die mit Flächeninhalten durchgeführt werden, können nun in unterschiedlicher Weise die Grundvorstellungen zu den Aspekten aufgegriffen und genutzt werden:
- Um Flächeninhalte direkt miteinander zu vergleichen, sind der Vereinigungs- und Kongruenzaspekt relevant, da die Flächen ggf. neu aufgeteilt werden müssen und dann mittels Übereinanderlegen gegeneinander abgeschätzt werden können.
- Um die Flächeninhaltsformel eines Rechtecks zu begründen, benötigt es den Maßzahlaspekt, da das Abzählen einbeschriebener Vergleichsquadrate wesentlich ist. Dies hängt auch eng mit der Grundvorstellung der Multiplikation als Rechteckflächeninhalt zusammen (siehe Abbildung 4.2).
- Für die Flächeninhaltsformel des Dreiecks sind wieder Kongruenz- und Vereinigungsaspekt relevant, da das Dreieck geeignet zerlegt und mit dem umschriebenen Rechteck verglichen werden muss (siehe Abbildung 7.5). Da Bezug zur Rechteckformel genommen wird, ist natürlich auch der Maßzahlaspekt relevant.
- Um Flächeninhalte zu approximieren, wie z. B. den eines Kreises (siehe Abbildung 7.6), benötigt es wieder alle drei Vorstellungen. So kann der Kreis in zueinander kongruente Teilflächen zerlegt werden (Kongruenz- und Vereinigungsaspekt), deren Gesamtflächeninhalt dann über die Rechteckformel näherungsweise bestimmt wird (Maßzahlaspekt).
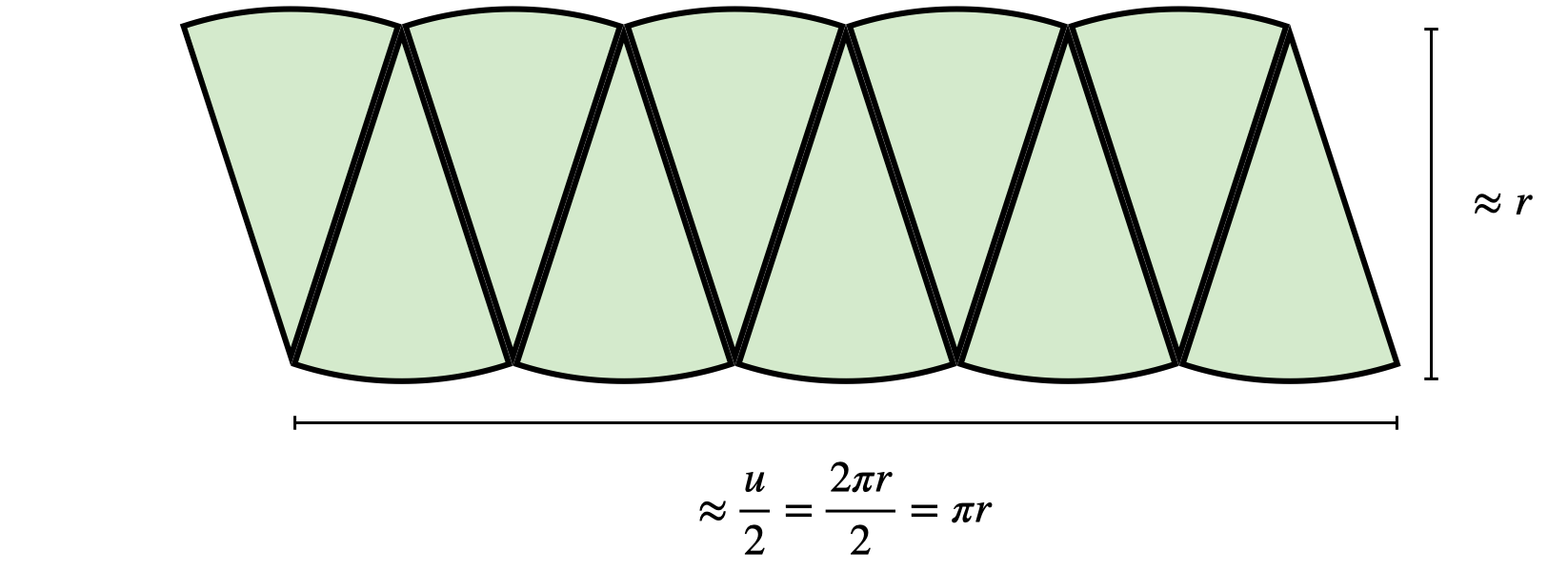
Abb. 7.6: Approximation des Kreisflächeninhalts
- Bei der Bestimmung von Oberflächeninhalten von Körpern, werden der Vereinigungsaspekt für die einzelnen Seitenflächen und ggf. der Kongruenzaspekt angesprochen, wenn es zueinander kongruente Seitenflächen gibt (wie z. B. bei Prismen), deren Flächeninhalte dann mit der entsprechenden Anzahl multipliziert und nicht einzeln ausgerechnet werden.
7.3.3 Auswirkungen auf Lernpfad
Der Lernpfad des Schulbuches greift diese fundamentale Idee und die Grundvorstellungen auf, indem zunächst Flächeninhalte (durch Auseinanderschneiden und Zusammenfügen) miteinander verglichen werden, anschließend das Auslegen mit normierten Flächenstücken erfolgt und daraufhin geeignete Maßeinheiten eingeführt werden und die Flächeninhaltsberechnung eines Rechtecks behandelt wird.
Die formale und empirische Ebene wurden hier getrennt dargestellt, was jedoch für eine stoffdidaktische Analyse gar nicht zwingend nötig ist. Entscheidend ist, dass Sie den ganzheitlichen Blick auf die aufgeworfenen Fragen haben und diese (zumindest in Teilen) beantworten können. Die getrennte Darstellung dient hier noch der Übersicht für Sie als Anfängerinnen und Anfänger im Umgang mit stoffdidaktischen Analysen – auch wenn darauf verzichtet wurde, die einzelnen Fragen schrittweise explizit zu beantworten.
7.4 Konkrete Ebene
Welche Kernfragen und Kernideen können die Entwicklung der Begriffe, Sachverhalte und Verfahren leiten?
Welche (inner- und außermathematischen) Kontexte sind geeignet, um an ihnen die Kernfragen und -ideen exemplarisch zu behandeln und die Inhalte zu rekonstruieren?
Wie kann das Verständnis sukzessive über realitätsbezogene Situationen in dem beabsichtigten Lernpfad konstruiert werden (vgl. horizontale Mathematisierung)?
Wie kann der Lernpfad in Bezug auf die mathematische Problemstruktur angeordnet werden (vgl. vertikale Mathematisierung)?
Als Kontext wählt das Schulbuch den Platzbedarf bei Tiergehegen im Zoo. Dieser Kontext ist aus mehreren Gründen besonders gut geeignet:
- In der Regel interessiert tatsächlich nur der Flächeninhalt des Geheges. Inhaltliche Verwechslungen mit dem Umfang oder dem Volumen können damit reduziert werden.
- Es ist aus dem Kontext heraus sinnstiftend, die Größe der Gehege miteinander zu vergleichen, da verschiedene Tiere einen unterschiedlichen Platzbedarf haben.20
- Verschiedene Formen der Tiergehege lassen sich nutzen, um verschiedene Vergleichsstrategien zu motivieren. So können z. B. Flächen zerlegt und neu zusammengesetzt werden, runde Formen angenähert werden und durch das Ausschneiden der Figuren ist ein Übereinanderlegen möglich.
Dabei werden zwei Kernideen aufgegriffen (Barzel et al., 2012a, 359 f.):
- Eine besteht im Vergleich der Flächeninhalte der verschiedenen Gehege. Dieses aus dem Kontext heraus begründbare Vorgehen führt im mathematischen Sinne zum Bedürfnis, Flächen zu vermessen, um sie miteiander vergleichen zu können. Als subjektive Kernfrage wird formuliert: »Wie kann ich die Größe von Flächen vergleichen?« (Barzel et al., 2012c, S. 170)
- Die zweite Kernidee ist das geschickte Bestimmen eines Flächeninhalts, wofür zunächst mittels Kästchenpapier das Auszählen von Flächen mit unterschiedlicher Genauigkeit diskutiert wird, anschließend geeignete Maßeinheiten eingeführt werden und die Flächeninhaltsformel des Rechtsecks behandelt wird. Die Formulierung der zugehörigen Kernfrage lautet: »Wie kann ich die Größe von Flächen geschickt bestimmen?« (Barzel et al., 2012c, S. 171)
Diese Ideen werden jeweils über die Prozesse des Erkunden, Ordnens und Vertiefens realisiert. Durch dieses Vorgehen21 wird das Verständnis sukzessive aufgebaut. Im Erkundungsprozess dient die Kernidee der Vorschauperspektive, während sie beim Ordnen und Vertiefen eher eine rückschauende Perspektive hat. Diese Objektivierung wird auch dahingehend sichtbar, dass die Kernfragen im Ordnen-Kapitel nun nicht mehr aus der Ich-Perspektive formuliert werden: »Wie kann man die Größe von Flächen vergleichen?«, »Wie kann man die Größe von Flächen bestimmen?« (Barzel et al., 2012c, 176 f.)
7.5 Ausblick auf empirische Ebene
Welche typischen individuellen Voraussetzungen (Vorstellungen, Kenntnisse, Kompetenzen, …) sind zu erwarten und wie passen diese zum angestrebten Verständnis?
Woher kommen typische Hindernisse oder unerwünschte Vorstellungen?
Wie können typische Vorkenntnisse und Vorstellungen als fruchtbare Anknüpfungspunkte dienen?
Welche Schlüsselstellen (Hindernisse, Wendepunkte, …) gibt es im Lernweg der Schülerinnen und Schüler?
Kuntze (2018, 159 f.) verweist auf typische Schwierigkeiten von Schülerinnen und Schülern im Umgang mit dem Flächeninhaltsbegriff.
So kommt es häufig zu einer Verwechslung zwischen Längenmaßen, Flächeninahlten und Volumina. Eine Ursache wird v. a. in der frühzeitigen kalkülhaften Herangehensweise gesehen, Flächeninhalte über Formeln berechnen zu müssen. So fehlt ein tiefergehendes Begriffsverständnis und die Formeln können nicht sinnstiftend genutzt werden. Dem kann u. a. dadurch begegnet werden, indem bewusst die Zusammenhänge hergestellt werden, z. B. zwischen Umfang und Flächeninhalt. Letztlich zeigen empirische Erhebungen, dass Kinder mit einem vertieften Verständnis über Flächeninhalte auch besser in der Lage sind, entsprechende Formeln anzuwenden (Wörner, 2014, S. 1330).
Weiterhin besteht wegen der Wortverwandtschaft von Fläche und Flächeninhalt die Gefahr, dass entsprechende Vorstellungen nicht aufgebaut werden, insbesondere dann, wenn die Begriffe (zumindest von der Lehrkraft) nicht sauber getrennt verwendet werden. Die Fläche ist die Figur an sich und wird über ihre Form bestimmt. Der Flächeninhalt ist ein Maß für die Größe der Figur (vgl. Barzel et al., 2012a, S. 362). Insbesondere für Schülerinnen und Schüler, deren Muttersprache nicht Deutsch ist, kann die fehlerhafte Verwendung dieser feinen Unterschiede hinderlich dabei sein, dem Unterricht zu folgen.
Derartige Schwierigkeiten werden im Schulbuch implizit aufgegriffen (z. B. strikte sprachliche Trennung) oder explizit thematisiert (z. B. verbindende und vergleichende Behandlung mit dem Umfang von Figuren), so dass auch dies wieder die Gestaltung des Lernpfades beeinflusst.
7.6 Zum Nachbereiten
- Finden Sie einen alternativen Kontext (statt den Zoogehegen) für Flächeninhalte, der die Forderungen nach Sinnstiftung erfüllt (siehe Definition 6.2).
- Diskutieren Sie, inwieweit sich aus dem Wissen über Grundvorstellungen zum Flächeninhalt die Gestaltung eines Arbeitsmittels ableiten lässt, das eine dieser Grundvorstellungen zum Begriff oder zu bestimmten Operationen mit Flächeninhalten unterstützt.
References
Um diesen Zusammenhang vollumfänglich zu verstehen, sind weiterhin der Vereinigungsapekt (Aufteilen in Teildreiecke) und der Maßzahlaspekt (um die Flächeninhaltsformel fürs Rechteck zu verstehen) nötig.↩︎
Verwiesen wird auch auf ein Gutachten über Mindestanforderungen an die Haltung von Säugetieren vom Bundesministerium für Ernährung und Landwirtschaft (2014).↩︎
Prediger et al. (2014) bezeichnen diese Prozesse auch als Kernprozesse des Unterrichtens.↩︎