1 Vier-Ebenen-Ansatz
Ziele
- Sie kennen typische Fragestellungen, um sich einer stoffdidaktischen Analyse systematisch zu nähern.
- Sie erkennen den Vier-Ebenen-Ansatz als eine Möglichkeit, eine stoffdidaktische Analyse strukturiert vorzunehmen.
- Sie können den Vier-Ebenen-Ansatz anhand eines Beispiels nachvollziehen.
- Sie sind sich der Komplexität einer stoffdidaktischen Analyse bewusst.
Material
- Folien zum Kapitel 1 (pdf, Keynote)
- App Winkel-Farm (nur für iOS)
1.1 Analyse von Lernbereichen
Die inhaltliche Basis der Veranstaltung bietet ein Beitrag von Hußmann & Prediger (2016) zur Spezifizierung und Strukturierung mathematischer Lernbereiche2. Nur einen Artikel als Basis einer kompletten 4 SWS starken Veranstaltung zu nutzen, scheint zunächst unüblich. In diesem Fall ist es jedoch hilfreich, da der Beitrag eine Kategorisierung stoffdidaktischer Analysen vorschlägt und vielfältige Fragen formuliert, woraus sich wieder ein ganzes Repertoir an Themen ergibt, die es im Rahmen von Vorlesung und Seminar zu untersuchen gilt.
Hußmann & Prediger (2016, 35 f.) kategorisieren eine stoffdidaktische Analyse in eine formale, semantische, konkrete und empirische Ebene, wobei diese nicht hierarchisch aufgebaut sind, sondern sich gegenseitig beeinflussen. Innerhalb der Ebenen wird jeweils noch einmal in die Spezifizierung und die Strukturierung eines Lerngegenstands unterschieden.
Auf der formalen Ebene wird der Lerngegenstand aus seiner fachlich-logischen Struktur heraus betrachtet.
Die semantische Ebene adressiert Sinn und Bedeutung des mathematischen Gegenstands sowie erkenntnistheoretische Aspekte.
Ziel der konkreten Ebene ist die Umsetzung des Lehr-Lern-Prozesses an konkreten Situationen, über die das mathematische Wissen konstruiert wird.
Über die empirische Ebene werden die kognitiven und ggf. sozialen Aspekte der Schülerinnen und Schüler in die stoffdidaktische Analyse integriert.
Über die Spezifizierung wird ermittelt, was genau Schülerinnen und Schüler bezüglich eines bestimmten mathematischen Themas lernen sollen, während die Strukturierung analysiert, wie diese Elemente miteinander in Verbindung stehen und wie sie im Lernpfad strukturiert werden können.
Aus den vier Ebenen und der jeweiligen Unterscheidung in Spezifizierung und Strukturierung ergeben sich acht (nicht immer trennscharfe) Dimensionen, die den Analyseprozess zu einem Lernbereich kategorisieren können. Um dies für Forschungs- und Entwicklungsprozesse greifbar zu machen, haben Hußmann & Prediger (2016, S. 36) typische Fragestellungen formuliert, an die in Tabelle 1.1 mehr oder weniger stark angelehnt wird.
| Spezifizierung | Strukturierung | |
|---|---|---|
| Formale Ebene | Welche Begriffe, Sachverhalte und Verfahren sollen erarbeitet werden? Wie können die Sachverhalte und Verfahren formal begründet werden? |
Wie kann das Netzwerk aus Begriffen, Sachverhalten und Verfahren logisch strukturiert werden? Welche Verbindungen zwischen den Fachinhalten sind aus fachlicher Perspektive entscheidend, welche weniger? |
| Semantische Ebene | Welche (mathematisch-gesellschaftliche) Bedeutung liegt hinter dem Lerngegenstand (vgl. Fundamentale Ideen)? Welcher Sinn soll bei den Schülerinnen und Schülern hinsichtlich des Lerngegenstands aufgedeckt werden und welche Repräsentationen sind dafür geeignet (vgl. Grundvorstellungen)? |
Wie verhalten sich Sinn und Bedeutung des Lerngegenstands zueinander und zu früheren und späteren Lerngegenständen? |
| Konkrete Ebene | Welche Kernfragen und Kernideen können die Entwicklung der Begriffe, Sachverhalte und Verfahren leiten? Welche (inner- und außermathematischen) Kontexte sind geeignet, um an ihnen die Kernfragen und -ideen exemplarisch zu behandeln und die Inhalte zu rekonstruieren? |
Wie kann das Verständnis sukzessive über realitätsbezogene Situationen in dem beabsichtigten Lernpfad konstruiert werden (vgl. horizontale Mathematisierung)? Wie kann der Lernpfad in Bezug auf die mathematische Problemstruktur angeordnet werden (vgl. vertikale Mathematisierung)? |
| Empirische Ebene | Welche typischen individuellen Voraussetzungen (Vorstellungen, Kenntnisse, Kompetenzen, …) sind zu erwarten und wie passen diese zum angestrebten Verständnis? Woher kommen typische Hindernisse oder unerwünschte Vorstellungen? |
Wie können typische Vorkenntnisse und Vorstellungen als fruchtbare Anknüpfungspunkte dienen? Welche Schlüsselstellen (Hindernisse, Wendepunkte, …) gibt es im Lernweg der Schülerinnen und Schüler? |
Diese Fragen können dabei helfen, einen Lernbereich aus professioneller Sicht vollumfänglich zu analysieren (insb. Spezifizierung) und daraus die Gestaltung eines Lernpfades für Schülerinnen und Schüler abzuleiten (insb. Strukturierung). Noch nicht abgeleitet werden kann daraus jedoch die Gestaltung einer konkreten Unterrichtsstunde – dies bedarf weiterer Überlegungen, z. B. zu Unterrichtsmethoden, Aufgaben, Klassenmanagement, … (Hußmann & Prediger, 2016, S. 37).
1.2 Lernbereich und Lerngegenstand
Als Lerngegenstände werden im Rahmen dieser Veranstaltung für spezifische Ausbildungszwecke ausgewählte Ausschnitte des gesellschaftlichen Wissens und Könnens angesehen (vgl. Lompscher, 1985). Diese Sichtweise entstammt tätigkeitstheoretischen Überlegungen, wobei zwischen gesellschaftlichem Wissen und Können und individuellen Kenntnissen, Fähigkeiten und Fertigkeiten unterschieden wird. Weitere Hintergrundinformationen dazu finden Sie in Abschnitt 5.1 sowie in den Kapiteln 8 und 8.3.
Zu Lerngegenständen gehören – im Rahmen des Mathematikunterrichts – sowohl inhaltliche Themen (wie der Satz des Pythagoras, Rechnen mit negativen Zahlen, …) als auch typische Methoden und Vorgehensweisen (wie das Modellieren, Problemlösen), aber auch Werte und Normen, die vermittelt werden sollen (z. B. dass in Rechnungen das Gleichheitszeichen untereinander geschrieben wird, handschriftliche Zeichnungen mit einem gespitzen Bleistift anzufertigen sind usw.).
Im Rahmen der Stoffdidaktik-Veranstaltung wird sich auf inhaltliche Themen konzentriert. Aber auch hier gibt es eine Fülle und potenzielle Kleinteiligkeit: So kann etwa das Einzeichnen einer gebrochenen Zahl auf dem Zahlenstrahl als eigener Lerngegenstand aufgefasst werden, aber auch die gesamte Bruchrechnung ist ein Lerngegenstand. Es bietet sich daher an, größere Cluster zu schaffen, die eines vergleichbaren Aufwands für die stoffdidaktische Analyse benötigen. Solche Cluster von Lerngegenständen sollen als Lernbereiche bezeichnet werden. Üblicherweise spiegelt sich ein Lernbereich dann in einer Unterrichtssequenz wieder (vgl. auch Vollrath & Roth, 2012, S. 187).
1.3 Beispiel Winkelbegriff
Um sich der Komplexität des Vier-Ebenen-Ansatzes bewusst zu werden, sollen mögliche Gedankengänge am Beispiel des Winkelbegriffs durchgeführt werden. Grundlage hierfür bietet die Dissertation Neue Zugänge zum Winkelbegriff (Etzold, 2021). In dieser wird zwar nicht der Vier-Ebenen-Ansatz für die stoffdidaktische Analyse verfolgt, aber dennoch lassen sich die einzelnen Elemente darin wiederfinden. Ziel ist hier keine vollumfängliche stoffdidaktische Analyse, sondern eher eine Darstellung der exemplarischen Herangehensweise, wie man sich einer Spezifizierung und Strukturierung des Lerngegenstands Winkel auf den vier Ebenen nähern kann.
1.3.1 Formale Ebene
Eine fachmathematische Analyse (bereits mit dem Blick auf eine schulische Nutzung) des Winkelbegriffs bieten u. a. Freudenthal (1973b), Strehl (1983) oder Mitchelmore (1990).
Freudenthal (1973b, S. 441) unterscheidet einen Winkel bspw. dahingehend, ob er über Geraden oder Halbgeraden (bzw. Strahlen) beschrieben wird, ob diese geordnet oder ungeordnet sind und ob sie in der orientierten oder unorientierten Ebene vorliegen (siehe Abbildung 1.1).
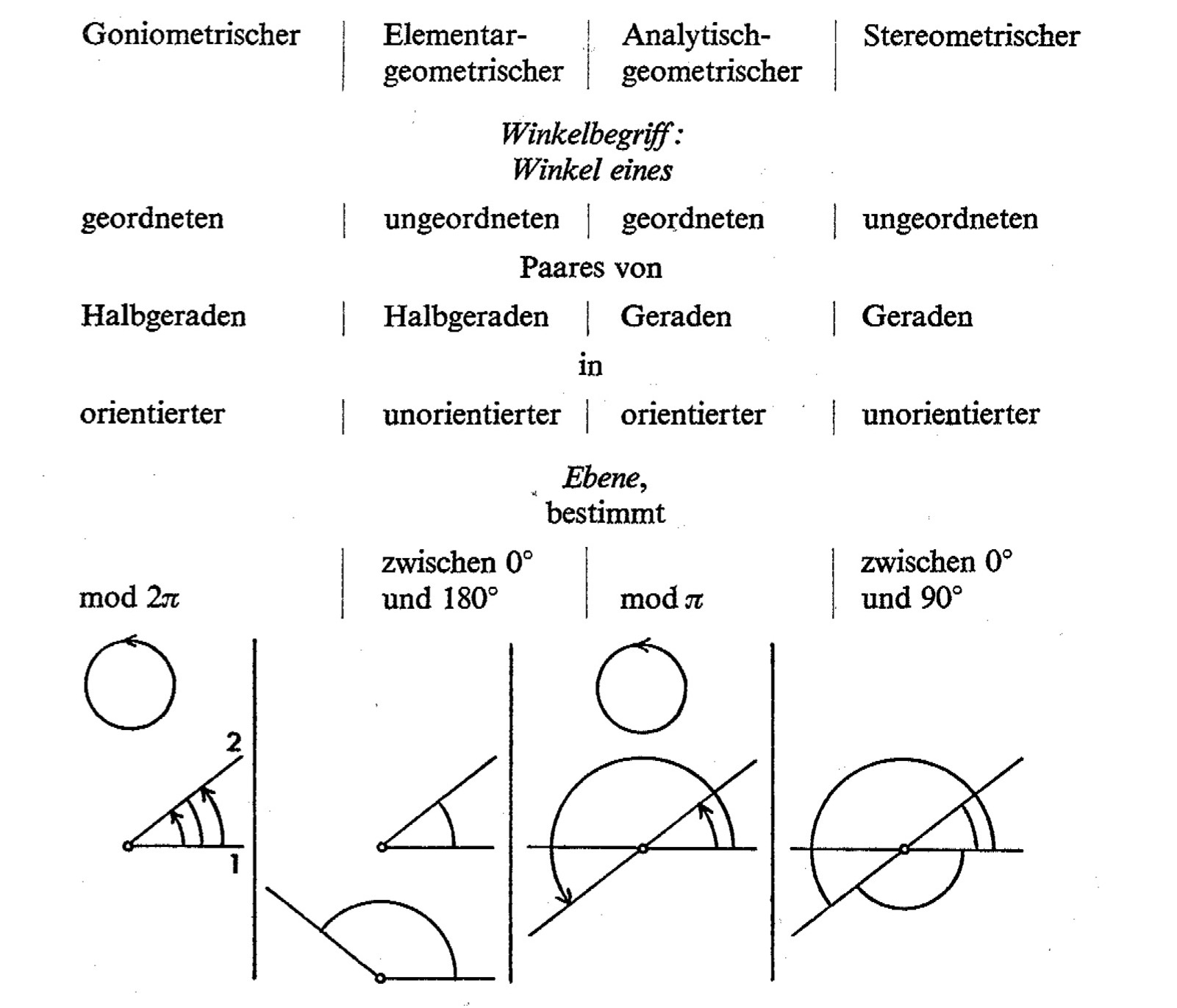
Abb. 1.1: Winkelbegriffe nach Freudenthal (1973b, S. 441)
Er diskutiert, welchen Einfluss die jeweilige Sichtweise auf dem Maßbereich hat, wie Winkel überhaupt gemessen werden können und wie mit Winkeln operiert werden kann. Was passiert denn, wenn man ein geordnetes Strahlenpaar in der orientierten Ebene spiegelt (vgl. Freudenthal, 1973b, 443 ff.)?
Wenn die Reihenfolge der Strahlen erhalten bleibt und die Winkelmessung aufgrund der Orientierung der Ebene vorgegeben ist, ändert sich damit ggf. auch das Maß des Winkels (siehe Abbildung 1.2).
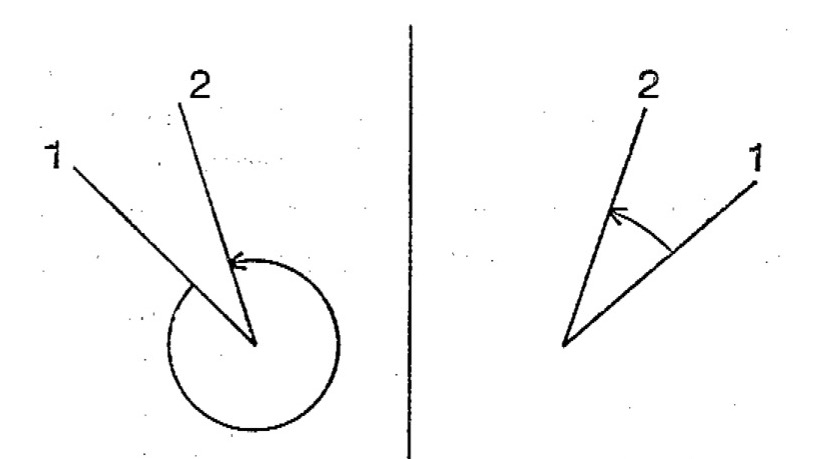
Abb. 1.2: Spiegelung eines goniometrischen Winkels (Freudenthal, 1973b, 443)
Hierzu stellt Freudenthal (1973b, 443 ff.) weitere fachmathematische Ausführungen dar und schließt damit, dass der elementargeometrische, goniometrische und analytische Winkelbegriff aus fachlicher Sicht für den schulischen Lernpfad unentbehrlich sind (Freudenthal, 1973b, S. 449).
Die Spezifizierung besteht also darin, den Begriff zu schärfen und Operationen mit ihm zu beschreiben. Die Strukturierung besteht u. a. in der vernetzenden Analyse der verschiedenen Winkelbegriffe und der Schlussfolgerung ihrer gleichermaßen Bedeutsamkeit für den Schulunterricht.
1.3.2 Semantische Ebene
Dazu, welche Vorstellungen Schülerinnen und Schüler zum Winkelbegriff entwickeln sollen, sei u. a. auf Krainer (1989) und Mitchelmore & White (1998) verwiesen. Eine grundsätzliche Schwierigkeit beim Unterrichten von Winkeln sind diverse und (scheinbar) nicht in Verbindung zu bringende Anwendungskontexte, die dennoch über denselben mathematischen Begriff beschrieben werden können. So ist das Sichtfeld eines Tieres ebenso wie die Umdrehung eines Wasserzählers über Winkel beschreibbar – haben doch beide Situationen zunächst nichts miteinander zu tun.
Aufbauend auf den Arbeiten von Krainer (1989) und Mitchelmore & White (1998) können über eine Verknüpfung zur formalen Ebene mithilfe einer informationstheoretischen Winkeldefinition (Etzold, 2021, 39 f..) vier Grundvorstellungen zum Winkelbegriff ausgearbeitet bzw. validiert werden:
- Winkel als Knick
- Winkel als Feld
- Winkel als Richtungsänderung
- Winkel als Umdrehung
Dabei erhalten die Bestandteile eines Winkels (Scheitelpunkt, Schenkel, ggf. Bereich zwischen den Schenkeln, Abweichungsmaß) eine besondere Bedeutung, über die sich auch eine sinnvolle Reihenfolge der Behandlung dieser Grundvorstellungen ableiten lässt. So »bietet es sich an, mit den Winkelfeldern zu beginnen. Bei diesen werden die meisten Bestandteile sichtbar (Scheitelpunkt, beide Schenkel als Begrenzungen sowie der zwischen den Schenkeln relevante Bereich) […]. Anschließend können Knicke oder Richtungsänderungen behandelt werden, woraufhin die Umdrehungen folgen.« (Etzold, 2021, S. 60)
Die Spezifizierung in diesem semantischen Teil ist demnach die Ausarbeitung der Grundvorstellungen. Die Begründung einer möglichen Reihenfolge kann der Strukturierung des Lerngegenstands zugeordnet werden.
1.3.3 Konkrete Ebene
Um die einzelnen Vorstellungen zu Winkeln aufzubauen, bedarf es charakteristischer Situationen, an denen der mathematische Kern der jeweiligen Vorstellung besonders gut sichtbar wird. Abbildung 1.3 zeigt derartige Winkelsituationen und die zugehörigen Grundvorstellungen (hier Winkelkontexte).
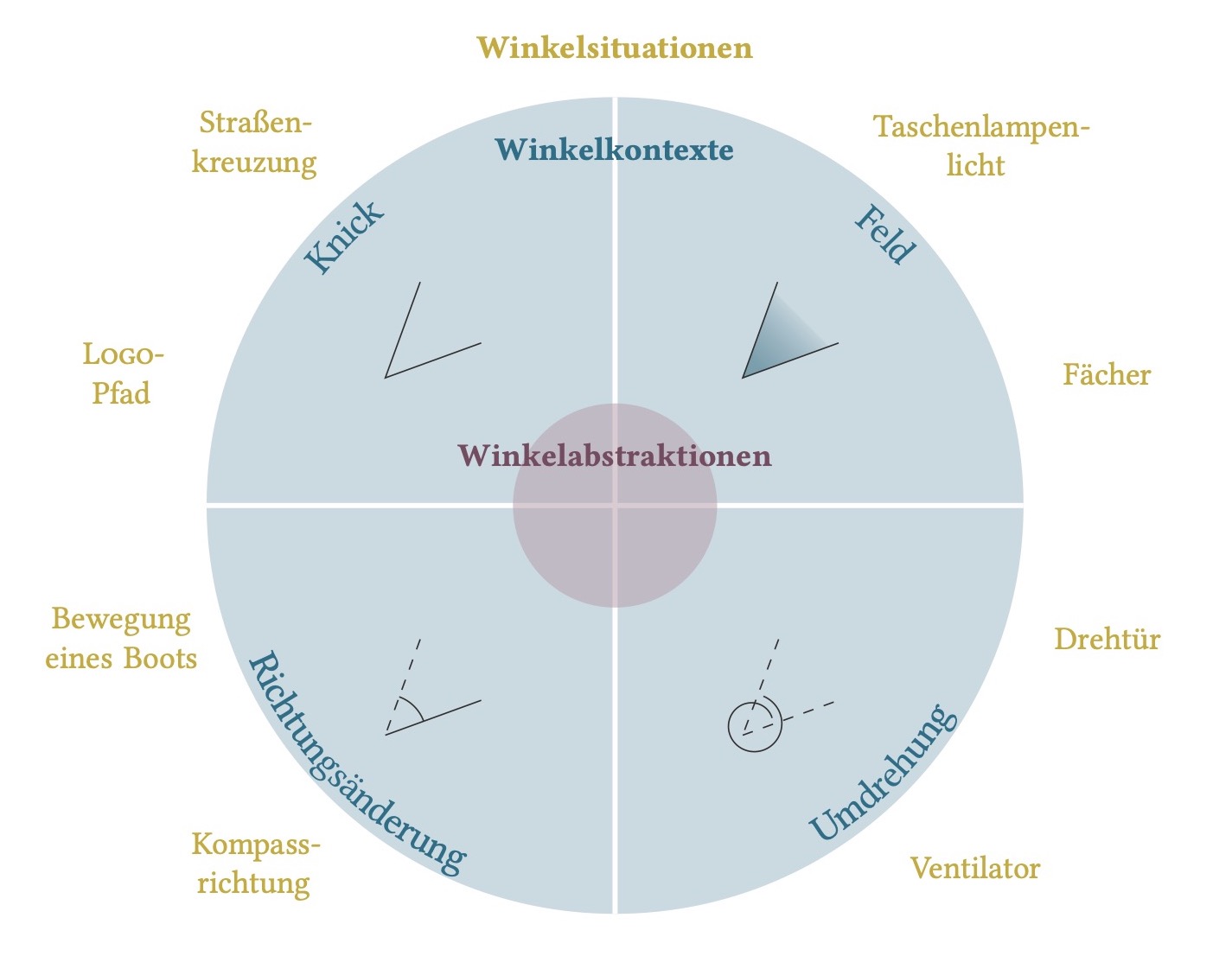
Abb. 1.3: Winkelsituationen und -kontexte (Etzold, 2021, S. 70)
Exemplarisch für die Grundvorstellung des Winkels als Feld wird darauf aufbauend eine Lernumgebung und darin eingebettetes Unterrichtsmaterial entwickelt, mithilfe dessen die Grundvorstellung ausgebildet werden kann. An der konkreten Situation der Sichtfelder von Tieren sollen die Schülerinnen und Schüler Handlungen ausführen, die es ihnen ermöglicht, den mathematischen Kern hinter dem konkreten Beispiel zu erkunden.
Die Schülerinnen und Schüler nutzen dazu eine App (siehe Abbildung 1.4), in der mehrere Tiere mit ihren Sichtfeldern dargestellt werden können, und erhalten u. a. folgende Aufgaben (vgl. Etzold, 2019b, S. 8 ff.):
- Setze das Schaf an eine Stelle, an der es von der Kuh gesehen wird, aber die Kuh selbst nicht sieht.
- Setze das Schaf an eine Stelle, an der es nicht von der Kuh gesehen wird.
- Das Schaf will die Kuh verwirren. Bewege es an möglichst viele Orte, an denen es von der Kuh gesehen wird.
- Setze das Schaf an eine Stelle, an der es noch gerade so von der Kuh gesehen wird.
- Wo muss das Schaf lang laufen, damit es die gesamte Zeit gerade so von der Kuh gesehen wird?
An Aufgabe 5 kann z. B. erkundet werde, dass sich das Schaf geradlinig auf der Grenze zwischen Sichtfeld und Nicht-Sichtfeld bewegen muss. In die eine Richtung ist die Bewegung beliebig fortsetzbar, in die andere durch den Kopf der Kuh begrenzt. Eine mathematische Verallgemeinerung dieser Handlung besteht dann in der Identifizierung des Schenkels (Begrenzung) als Strahl (nur in eine Richtung fortsetzbar) mit dem Scheitelpunkt (Kopf der Kuh) als Quelle des Winkelfeldes.
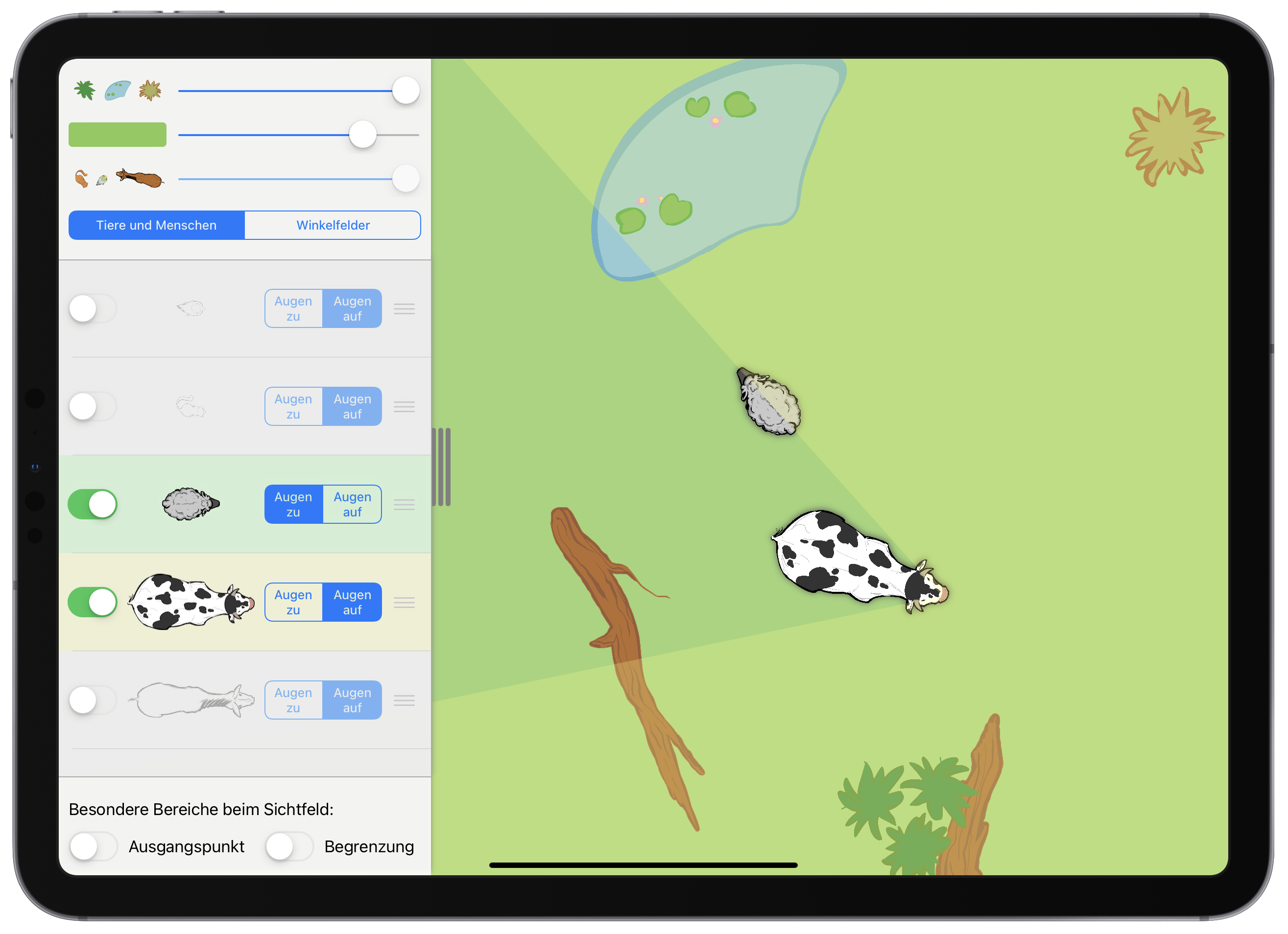
Abb. 1.4: Screenshot der App Winkel-Farm (Etzold, 2019a)
Als Spezifizierung kann das Finden der Sichtfeld-Situation als charakterisches Beispiel für ein Winkelfeld angesehen werden. Die Strukturierung führt zum dargestellten Lernpfad und den konkreten Aufgabenstellung, über die konkrete Handlungen verallgemeinert werden und damit das mathematische Verständnis aufgebaut wird.
1.3.4 Empirische Ebene
Die zuvor beschriebene Lernumgebung wurde in mehreren Zyklen erprobt und dabei die Qualität der Handlungen der Schülerinnen und Schüler beobachtet. Ein Ziel bestand darin, dass möglichst verallgemeinerbare Handlungen (wie oben am Beispiel des Schenkels beschrieben) durchgeführt werden.
Es wird erwartet, dass die Repräsentation eines Sichtfeldes von der Draufsicht über eine semintransparent ausgemalte Teilfläche der Ebene noch nicht bekannt ist. Um diese nachzuvollziehen und mit eigenen Erfahrungen in Bezug zu bringen, wird an den Beginn der Unterrichtsstunde ein Bild des Klassenraumes in der Draufsicht präsentiert (siehe Abbildung 1.5). Dann soll eine Schülerin oder ein Schüler beschreiben, was sie/er alles sieht, ohne den Kopf zu drehen. Dieser Bereich wird auf dem Bild eingezeichnet, so dass die Repräsentation des Sichtfeldes im Folgenden zur Verfügung steht.
Abb. 1.5: Klassenraum von oben (Foto: Christian Dohrmann)
In der Erprobung konnte beobachtet werden, dass einige Bedienschwierigkeiten mit der Anwendung den Lernfortschritt hemmten. Dies konnte u. a. dadurch verbessert werden, dass vor die eigentliche Erarbeitung eine freie Erkundungsphase mit der App (siehe Abbildung 1.6) gesetzt wurde (Etzold, 2021, S. 147, 152). Durch spezifische Aufgabenstellungen wurden bestimmte Funktionen der App fokussiert:
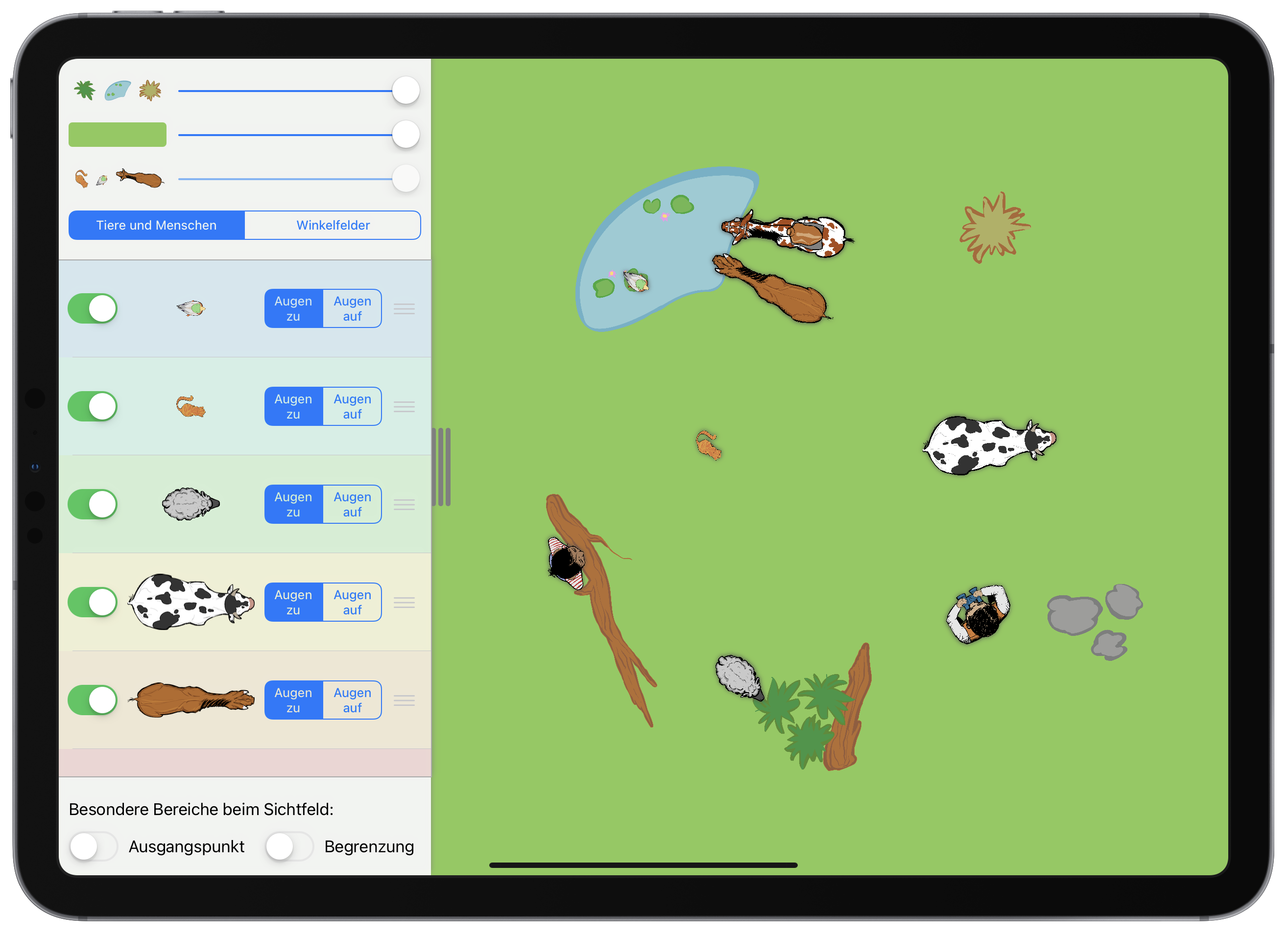
Abb. 1.6: Möglicher Startbildschirm für die freie Erkundungphase
»Das Pferd soll auf dem Steinpflaster stehen, die Frau soll auf dem Pferd sitzen/stehen. Das Pferd guckt in Richtung der grünen Büsche, die Frau hat die Augen zu. Gleichzeitig versteckt sich die Katze unter der Kuh.«
Die Einführungsphase über das Klassenraumfoto folgt aus der Spezifizierung innerhalb der empirischen Ebene. Das Hinzufügen der freien Erkundungsphase ist dagegen der Strukturierung der Analyse zuzuordnen.
1.3.5 Verknüpfung der Ebenen
An den Ausführungen ist schon sichtbar geworden, dass sich die Ebenen nicht immer trennen lassen und teilweise gegenseitig beeinflussen. Auch gehen oft Spezifizierung und Strukturierung ineinander über.
Das ist aber gar nicht schlimm, ganz im Gegenteil. Es zeigt wieder einmal, wie wichtig solch ein ganzheitlicher Ansatz ist, so dass eine stoffdidaktische Analyse aus den diversen Sichtpunkten heraus betrachtet werden sollte.
Wichtig ist v. a., dass Sie sich als Lehrkraft stets darüber im Klaren sind, dass für eine stoffdidaktische Analyse verschiedene Perspektiven verfolgt werden müssen. Sehen Sie den Vier-Ebenen-Ansatz daher auch als Kontrollinstrument, ob Sie an alles gedacht haben, wenn Sie einen Lerngegenstand intensiv analysieren.
1.4 Zum Nachbereiten
- Lesen Sie den Artikel von Hußmann & Prediger (2016) zum Vier-Ebenen-Ansatz.
- Reflektieren Sie Ihre bisherige Fach- und Fachdidaktikausbildung in Mathematik dahingehend, welche der aufgeworfenen Fragen Sie zu konkreten Themenbereichen (nicht) beantworten könnten.