7 Begriffe, Zusammenhänge, Verfahren

Ziele

• Sie kennen prinzipielle Möglichkeiten, Begriffe, Zusammenhänge und Verfahren einzuführen, Aneignungsprozesse mithilfe von Orientierungshilfen zu gestalten und die Inhalte zu festigen.
  
• Sie erkennen Gemeinsamkeiten und Unterschiede in den typischen Vorgehensweisen für Begriffe, Zusammenhänge und Verfahren.
  
• Sie können die Prozesse tätigkeitstheoretisch einordnen.

Material

• Folien zum Kapitel 7 (pdf, Keynote)

Aufbauend auf den tätigkeitstheoretischen Grundlagen der letzten beiden Kapitel soll in diesem Kapitel dargestellt werden, wie damit das Unterrichten von Begriffen, Zusammenhängen und Verfahren gestaltet werden kann. Dabei wird immer von drei Schritten ausgegangen:

1. Begriff/Zusammenhang/Verfahren erarbeiten
   
2. Begriff/Zusammenhang/Verfahren aneignen über die Nutzung geeigneter Orientierungshilfen sowie der etappenweisen Ausbildung geistiger Handlungen
   
3. Begriff/Zusammenhang/Verfahren festigen

Perspektivisch sollten Sie in der Lage sein, die hier beschriebenen Prozesse auf konkrete Lerngegenstände anzuwenden. Dabei ist jedoch zu beachten, dass es sich nicht um eine feste Vorgehensweise handelt, sondern vielmehr prinzipielle Gestaltungsmöglichkeiten für die Stofferarbeitung und Festigung beschrieben werden.

7.1 Begriffe

»Man spricht allgemein von einem ›Begriff‹, wenn eine Anzahl von Objekten oder Ereignissen aufgrund gewisser übereinstimmender Merkmale mit einem gemeinsamen Namen belegt wird« (Weinert, 1974, S. 664, zitiert nach Zech, 1998, S. 165).

Damit werden zwei Dimensionen von Begriffen sichtbar, nämlich der Bezeichner und das Bezeichnete. Während der Bezeichner das Wort bzw. der Name ist, mit dem das zu betrachtende Objekt oder Ereignis belegt wird, ist das Bezeichnete die Idee hinter dem Objekt, also das Gefüge an übereinstimmenden Merkmalen. Weder Bezeichner noch Bezeichnetes sind jedoch das Objekt oder Ereignis selbst. Äquivalente, und auch in den Sprachwissenschaften bedeutsame Bezeichnungen sind Signifikant für den Bezeichner und Signifikat für das Bezeichnete (vgl. auch Rembowski, 2015, 13 ff.; Wikipedia, 2021c, 2021b).

Wenn etwa ein Kind den Bezeichner Quader verwendet, um ein Viereck mit vier gleich langen Seiten und vier rechten Winkeln zu beschreiben (also eigentlich das Bezeichnete eines Quadrates meint), kann es sich hier durchaus um eine Wortverwechslung handeln, die nicht zwingend mit einem inhaltlichen Fehlverständnis einhergehen muss.

7.1.1 Begriffe bilden

Die Einführung von Begriffen kann stets als Wechselspiel zwischen Beispielen/Gegenbeispielen und der Begriffsfestlegung aufgefasst werden. Die Richtung und Qualität dieses Zusammenhangs ermöglicht verschiedene Wege zum Begriff (siehe Abbildung 7.1).

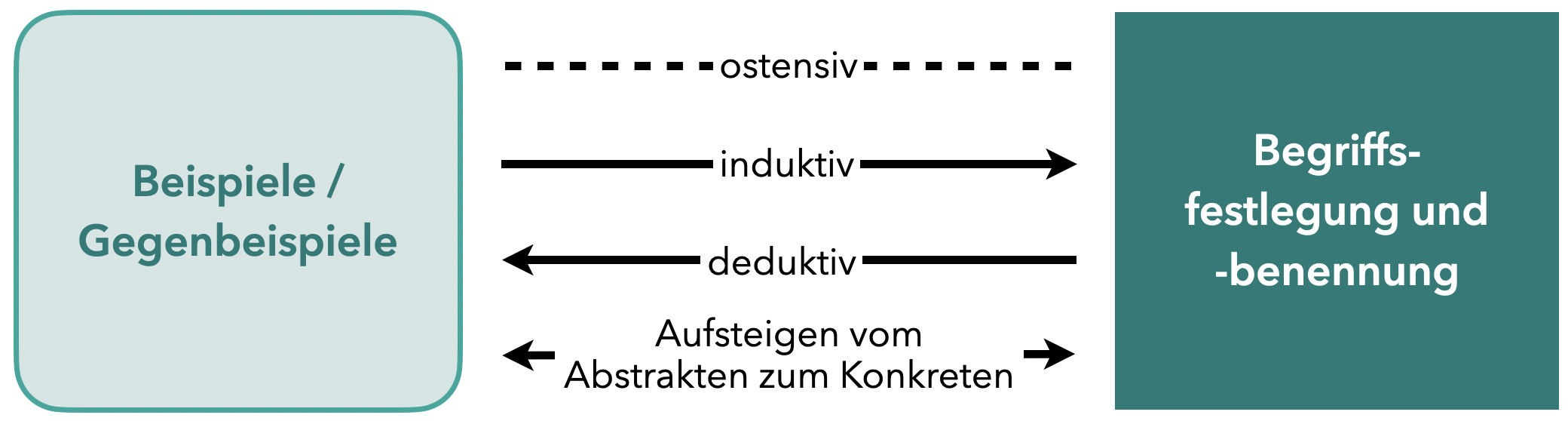
Abb. 7.1: Möglichkeiten der Begriffseinführung

7.1.1.1 Ostensive Begriffseinführung

Bei der ostensiven Begriffseinführung wird das Lernen eines Begriffs als Erfassen der Gestalt als einprägsames Ganzes angenommen. Das heißt, der Begriff wird gar nicht formal definiert, sondern nur über Beispiele dargestellt. Dies wird insbesondere bei Arbeitsbegriffen so gehandhabt (z. B. Bruchstrich) oder bei der Begriffseinführung in der Grundschule, wenn deren Gestalt leicht eingänglich ist (z. B. Kreis).

Dabei muss jedoch die wahrgenommene Gestalt dem Wesentlichen des Begriffs entsprechen und der Gestalteindruck ist häufig abhängig von der Lage. Es ist also darauf zu achten, nicht ausschließlich Spezialfälle zu präsentieren, die dann zu einer Untergeneralisierung des Begriffs führen. Werden z. B. zwei zueinenander senkrechte Strecken präsentiert, sollten diese also nicht gleich lang sein, sich nicht in der Mitte schneiden und auch nicht parallel zu den Tafel-/Blatt-/Bildschirmrändern ausgerichtet sein (siehe Abbildung 7.2).

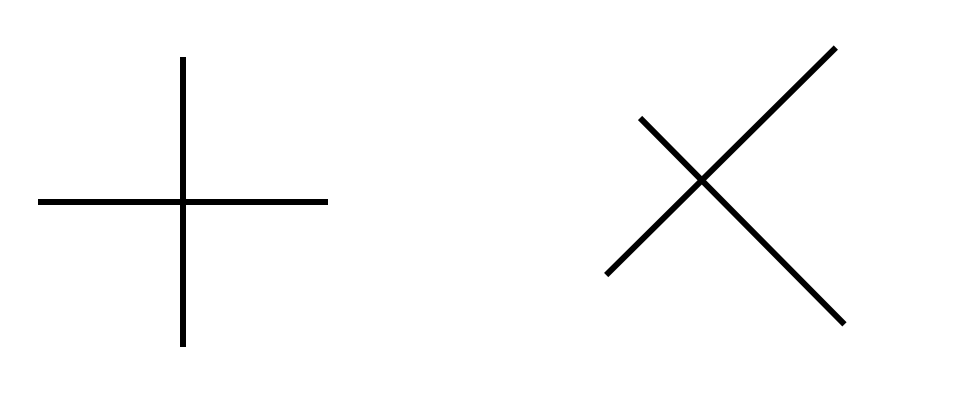
Abb. 7.2: Ungeeignete und geeignete ostensive Darstellung des Begriffs senkrecht zueinander

7.1.1.2 Induktive Begriffseinführung

Bei der induktiven Begriffseinführung wird zunächst eine Vielzahl an Beispielen präsentiert. Aus diesen heraus wird dann das Wesentliche des Begriffs extrahiert. Dafür werden die Objekte zunächst beschrieben und anschließend gemeinsame Eigenschaften entdeckt. Dies kann passieren, indem die ungeordneten Beispiele nach Merkmalen sortieren werden oder bereits in Teilmengen aufgeteilt präsentiert werden. Daran wird nun der Begriffsinhalt herausgearbeitet.

Dieses Vorgehen ist relativ natürlich, da es auch der Begriffsbildung im Vorschulalter bzw. im Alltag entspricht. Allerdings benötigt es sehr viel Zeit. Hinzu kommt, dass das Erkennen der gemeinsamen Merkmale in der Unterrichtssituation nicht selten zu einem Ostereiersuchen verfällt, indem die Lehrkraft so lange nachfragt, bis die gewünschte Eigenschaft gefunden wird. Oder noch kritischer formuliert: »Die Lernenden jedoch haben noch keine Ahnung von diesem Wesen und können sie auch nicht gewinnen, da sie keinerlei Mittel dafür besitzen« (Giest & Lompscher, 2004).

Beim Einsatz der induktiven Begriffseinführung müssen also insbesondere geeignete Impulsfragen im Vorhinein bedacht werden, um die Schülerinnen und Schüler durch gezielte Fragestellungen das Wesentliche des Begriffs entdecken lassen zu können.

7.1.1.3 Deduktive Begriffseinführung

Die deduktive Begriffseinführung geht den Weg von der Definition zu den Beispielen. Dieses Vorgehen ist das übliche in der Hochschulmathematik und sollte – um zum Beispiel wissenschaftspropädeutisch tätig zu sein – auch im Schulunterricht schon vermittelt werden.

Typische Impulsfragen für das anschließende Identifizieren udn Realisieren von Repräsentanten¹⁹ bei der deduktiven Begriffseinführung nach Gabe der Definition zu unterstützen, können sein:

• Ist das ein …?
• Stelle ein … her.
• Welche Teile der Definition sind nicht erfüllt?
• Was muss an dem … verändert werden, damit es ein … ist?
• Wie prüft man, ob das ein … ist?
• Warum entsteht ein …, wenn man das so und so herstellt?

7.1.1.4 Aufsteigen vom Abstrakten zum Konkreten

Das Aufsteigen vom Abstakten zum Konkreten ist durch ein spezifisches Wechselspiel von einem Beispiel, der Definition und weiterer Beispiele geprägt. Nach Lompscher (1996) sind drei Schritte relevant.

Abb. 7.3: Aufsteigen vom Abstrakten zum Konkreten

1. Für die Einführung des Begriffs wird ein konkretes Ausgangsbeispiel gewählt, an dem das Wesen des Begriffs besonders gut deutlich wird. An diesem Ausgangskonkretum werden Lernhandlungen erarbeitet, die sich zwar am Beispiel orientieren, aber verallgemeinern lassen, sodass sie dem Begriffsaufbau dienlich sind.

2. Im Anschluss wird, mit Unterstützung der Lehrkraft, das Wesen des Begriffs herausgearbeitet und in Form einer Ausgangsabstraktion formuliert. Dieses Vorgehen ist vergleichbar mit dem induktiven Begriffserwerb, allerdings wird nicht aus einer Vielzahl von Beispielen eine gemeinsame Eigenschaft eliminiert, sondern am charakteristischen Beispiel wird die Eigenschaft durch eine wissende Person (Lehrkraft) in Bezug auf die Handlungserfahrungen der Schülerinnen und Schüler dargestellt. Dieser Prozess kann durch Orientierungshilfen oder Arbeitsmittel (siehe nächstes Kapitel) unterstützt werden.

3. Der dritte Schritt, das eigentliche Aufsteigen vom Abstrakten zum Konkreten, ist nun das Abarbeiten von Konkretisierungsreihen. Hierzu werden weitere Beispiele für den Begriff betrachtet, auf die das Ausgangsabstraktum angewandt wird. Orientierungshilfen/Arbeitsmittel dienen dabei als Mittler und die Lernhandlungen werden in verallgemeinerter und ggf. auch modifizierter Form angewandt. Erst auf diese Weise ist ein echtes Durchdringen des Begriffs möglich. Dieses Vorgehen ist mit dem deduktiven Vorgehen vergleichbar, allerdings nicht im dem Sinne, dass aus einer Definition heraus die Beispiele generiert werden. Vielmehr wird auf gegebene Beispiele die Definition angewandt, ausgeschärft und damit der Begriff immer besser verstanden.

Diese Vorgehensweise hat den Vorteil, relativ effektiv zu sein und trotz des Verzichts auf ein deduktives Vorgehen recht schnell zu einer (ersten) Definition des Begriff zu kommen. Außerdem ist sie ehrlich gegenüber den noch nicht vorhandenen Kenntnissen der Schülerinnen und Schüler, da diese bei einem induktiven Vorgehen i. d. R. noch nicht wissen, nach welchem gemeinsamen Merkmal die Beispiele nun analysiert werden sollen, so dass es oft mit einem Raten (oder letztlich doch einer Vorgabe durch die Lehrkraft) verbunden ist, auf das zu interessierende Merkmal zu stoßen.

7.1.1.5 Beispiele und Gegenbeispiele

Unabhängig davon, auf welche Art und Weise man Begriffe einführt, ist stets ein Zusammenspiel aus Beispielen, Gegenbeispielen und verbalen Erläuterungen notwendig – und das in allen Altersklassen! Bei entsprechenden Verbalisierungen sind ggf. weniger Beispiele/Gegenbeispiele nötig, da damit das Wesen des Begriffs besser herausgearbeitet werden kann (Zech, 1998, S. 260).

Bei der Auswahl von Beispielen und Gegenbeispielen bieten sich das Variationsprinzip und das Kontrastprinzip an. Die folgenden Überlegungen stammen hauptsächlich von Zech (1998, 260 ff.).

7.1.1.5.1 Variationsprinzip

Beispiele sollten breit variiert werden, es darf nicht zu einer Untergeneralisierung kommen. Im Alltag als Gegenbeispiele empfundene Beispiele müssen mit angebracht werden. Wichtig erscheinende irrelevante Merkmale sollten mindestens einmal variiert werden.

Für den Rechtecktbegriff kann dies eine Variation in Größe, Seitenverhältnis, Ausrichtung und Farbe, aber auch die Präsentation von Spezialfällen (z. B. eines Quadrates) bedeuten (siehe Abbildung 7.4).

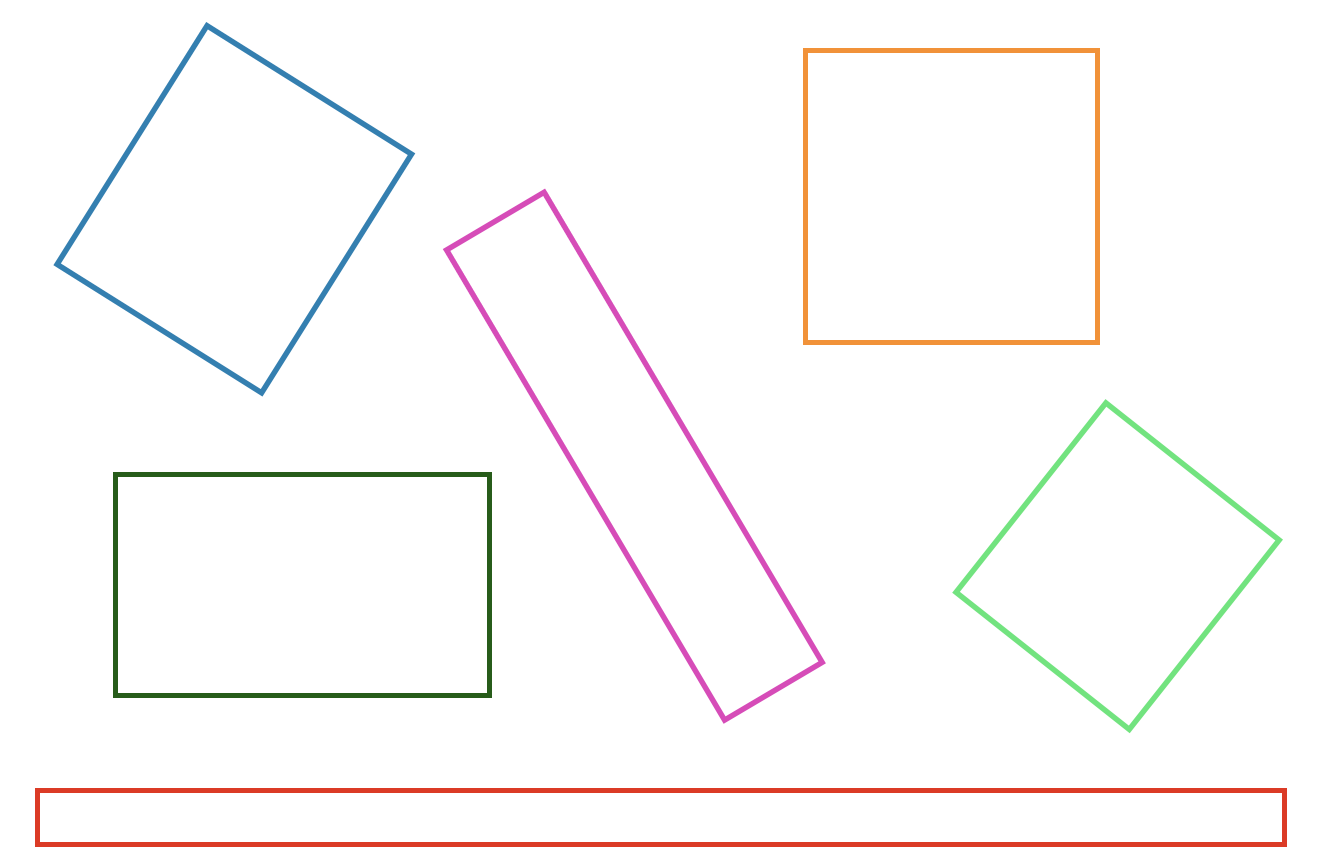
Abb. 7.4: Variationsprinzip beim Begriff Rechteck

Um dieses Prinzip für einen Begriff zu realisieren, muss man sich als Lehrkraft also Gedanken über die mathematisch relevanten und irrelevanten Eigenschaften machen. Auch eine explizite Diskussion mit den Schülerinnen und Schülern, warum diese Eigenschaften variiert werden durften (und andere nicht), kann hilfreich für das Begriffsverständnis sein.

7.1.1.5.2 Kontrastprinzip

Gegenbeispiele dürfen nicht für Beispiele gehalten werden, es darf nicht zu einer Übergeneralisierung kommen. Im Alltag als Beispiele empfundene Gegenbeispiele (sogenannte Fastbeispiele) müssen diskutiert werden. Relevante Merkmale müssen mindestens einmal fehlen.

Für den Rechteckbegriff relevant sind etwa die rechten Winkel (was bei Beibehaltung der gleich langen, parallelen Seiten zu einem Parallelogramm führt). Auch die Ecken-Eigenschaften und die Tatsache, dass es sich um eine Figur (und nicht um einen Körper) handelt, sind relevant (siehe Abbildung 7.5).

Abb. 7.5: Kontrastprinzip beim Begriff Rechteck

7.1.1.5.3 Darbietung von Beispielen und Gegenbeispielen

Zech (1998, S. 261) fasst zusammen: »Beispiele und Gegenbeispiele sind dann am effektivsten, wenn sich die Beispiele möglichst stark in den irrelevanten Merkmalen unterscheiden und die Gegenbeispiele in möglichst wenigen relevanten Merkmalen unterscheiden.«

Eine simultane Darbietung zweier stark kontrastierender Beispiele (Abbildung 7.6) oder eines Beispiels mit einem sehr ähnlichen Gegenbeispiel (Abbildung 7.7) kann weiterhin den Fokus auf die relevanten Merkmale des Begriffs lenken.

Abb. 7.6: Simultane Darbietung zweier Beispiele zum Begriff Quadrat

Abb. 7.7: Simultane Darbietung von Beispiel und Gegenbeispiel zum Begriff Achsensymmetrie

7.1.2 Begriffe aneignen

Die relevanten Aneignungshandlungen beim Begriffserwerb sind das Identifizieren und Realisieren. Die Tabelle konkretisiert die Möglichkeit der Gestaltung von Orientierungshilfen und das etappenweise Ausbilden geistiger Handlungen an diesen beiden Aneignungshandlungen.

Tab. 7.1: Teilprozesse zur Begriffsbildung und -aneignung, nach Steinhöfel et al. (1988, S. 46)

	Identifizieren	Realisieren
Orientierungshilfen	System der Merkmale des Begriffs; Schrittfolge zum Prüfen der Merkmale	Handlungsvorschrift zum Herstellen oder Vervollständigen des Objekts
Etappe der materiellen/materialisierten Handlung	Überprüfung der Merkmale an gegebenen Objekten oder an Modellen (Zeichnungen, Diagramme); Orientierungshilfe liegt schriftlich vor	Beim Lösen entsprechender Aufgaben orientieren sich Schülerinnen und Schüler am Text der Handlungsvorschrift, die schriftlich vorliegt.
Etappe der sprachlichen Handlung	sprachliches Begründen des Zutreffens oder Nichtzutreffens der einzelnen Merkmale (unter zunehmender Zurückdrängung der Orientierungshilfe)	Kommentieren des Lösungsweges beim Ausführen der Handlungsschritte (Handlungsvorschrift liegt nicht mehr vor)
Etappe der geistigen Handlung	sofortiges Entscheiden, ob der Begriff zutrifft oder nicht (ohne Benutzung der Orientierungshilfe)	selbstständiges Lösen entsprechender Aufgaben (ohne Verwendung der Handlungsvorschrift)

7.1.3 Begriffe festigen

Vertiefende Übungen ergeben sich v. a. durch die Einordnung des neu erlernten Begriffs in ein Begriffssystem. Hinzu kommt die Verwendung alternativer Definitionen sowie die Variablität in der Verwendung von Bezeichnungen (z. B. Variablen). Auch können Grenz- und Sonderfälle des Begriffs diskutiert werden, um ein vertieftes Verständnis zu gewinnen (vgl. Steinhöfel et al., 1988, S. 34). Eine systematische Übersicht, auch für ein ähnliches Vorgehen bei Sachverhalten und Verfahren, bietet Tabelle 7.3.

Nach Vollrath & Roth (2012, S. 48) ist ein Begriff verstanden, wenn Schülerinnen und Schüler

• die Bezeichnung des Begriffs kennen,
• Beispiele angeben und jeweils begründen können, weshalb es sich um ein Beispiel handelt,
• begründen können, weshalb etwas nicht unter den Begriff fällt,
• charakteristische Eigenschaften des Begriffs kennen,
• Oberbegriffe, Unterbegriffe und Nachbarbegriffe kennen,
• mit dem Begriff beim Argumentieren und Problemlösen arbeiten können.

7.2 Zusammenhänge

Bei Zusammenhängen (also Regeln, Gesetzen und Sätzen) bietet es sich an, in der Erarbeitung zwischen dem Finden des Zusammenhangs, dem Finden einer Begründung und der Darstellung der Begründung zu unterscheiden.²⁰ Im schulischen Kontext erfüllt eine Begründung i. d. R. nicht nur die Funktion, den Wahrheitsgehalt des Sachverhaltes zu sichern (diese Funktion hat ein Beweis v. a. in der Fachmathematik), sondern über die Begründung den Sachverhalt besser zu verstehen, dessen innere Struktur nachzuvollziehen und mithilfe der Begründung über den Sachverhalt zu kommunizieren. Während die ersten beiden Teilprozesse v. a. der Erarbeitung des Sachverhalts dienen, sind alle drei Teilprozesse notwendige Bestandteile für die Aneignung des Sachverhalts.

7.2.1 Zusammenhänge erarbeiten

7.2.1.1 Zusammenhänge finden

Für das Finden neuer Zusammenhänge bestehen folgende Möglichkeiten (vgl. Vollrath & Roth, 2012, 247 f.):

• Der neue Zusammenhang wird induktiv über das Entdecken von Merkmalen in gegebenen Situationen erarbeitet.

  Werden bspw. Rechtecke und ihre Diagonalen gezeichnet, kann daraus entdeckt werden, dass sich die Diagonalen stets halbieren, dies also ein gültiger Zusammenhang zu sein scheint.

• Der neue Zusammenhang entsteht aus dem Widerspruch zu einer angenommenen Hypothese.

  Aus dem Recheckbeispiel könnte angenommen werden, dass Vierecke mit sich halbierenden Diagonalen immer Rechtecke sind. Über ein Gegenbeispiel kann aber gezeigt werden, dass dies auch bei Parallelogrammen der Fall ist. So wurde ein neuer Zusammenhang entdeckt.

• Der neue Zusammenhang wird deduktiv aus bisherigen Zusammenhängen gefolgert.

  Der Kosinussatz kann über die Zerteilung eines allgemeinen Dreiecks in rechtwinklige Dreiecke und die mehrfache Anwendung des Satzes des Pythagoras gefolgert werden.

Nicht immer ist es sinnvoll, einen Zusammenhang zu finden. So kann etwa die Lösungsformel \(x_{1,2} = -\frac{p}{2}\pm \sqrt{\left(\frac{p}{2}\right)^2-q}\) schlecht vermutet werden, um damit die Gleichung \(0 = x^2+px+q\) zu lösen. In dem Fall wird üblicherweise mithilfe einer Herleitung direkt zur Begründung des Zusammenhangs übergegangen. Ein solches Vorgehen ist i. d. R. deduktiv.

7.2.1.2 Begründungen finden

Da das Finden von Begründungen als Problemlöseprozess aufgefasst werden kann, ist es notwendig, auf Heurismen²¹ Bezug zu nehmen, um Begründungen für Zusammenhänge zu finden (vgl. Steinhöfel et al., 1988, 67 ff.).

• Dazu gehören heuristische Strategien, wie das Vorwärts- und Rückwärtsarbeiten, Rückführung von Unbekanntem auf Bekanntes oder Analogieschlüsse, die einzelne Beweisschritte leiten könnten.
• Heuristische Hilfsmittel wie informative Figuren können den Lösungsweg erleichtern. Gerade das Einzeichnen von Hilfslinien hat für geometrische Beweise eine hohe Bedeutung und sollte entsprechend erarbeitet werden.
• Über eine Zusammenstellung wichtiger Zusammenhänge und Definitionen stehen notwendige Beweismittel zur Verfügung, die dann auch auch Orientierungshilfen dienen können.

7.2.2 Zusammenhänge aneignen

Für die Aneignung eines neuen Zusammenhangs muss dieser an sich sowie seine Begründung angeeignet werden. Da beides eng miteinander zusammenhängt, sollte der Fokus daher auf der inneren Struktur des Zusammenhangs liegen. Mögliche Lernhandlungen hierfür sind:

• Prüfen der Voraussetzungen, um die Anwendbarkeit und Gültigkeit der Behauptung zu schließen. Dies erfolgt i. d. R. anhand einer (in einer Aufgabe) gegebenen Situation. Es reicht nicht aus, den Zusammenhang nur anzuwenden, sondern das Prüfen der ihm zugrundeliegenden Voraussetzungen ist ein wesentlicher Schritt in dessen Aneignung. Im Endeffekt entspricht dieses Prüfen einer Identifizierungshandlung.
• Angeben von Beispielen, auf die der Zusammenhang anwendbar ist. Dies kann auch als Realisierungshandlung aufgefasst werden.
• Herausarbeiten von Voraussetzung und Behauptung, um die Aussage des Zusammenhangs zu verinnerlichen und dessen logische Struktur zu betonen. Dies kann auch über eine sprachliche Umformulierung des Zusammenhangs (z. B. als Wenn-dann-Aussage) erfolgen.

Als Orientierungshilfen innerhalb der genannten Lernhandlungen und zur Darstellung der Begründung sind geeignet:

• In strukturierten Wissensspeichern kann ein Zusammenhang oder eine Gruppe von Zusammenhängen so dargestellt werden, dass dessen/deren innere Struktur hervorgehoben wird. Hierzu bietet sich eine tabellarische Übersicht an, die neben dem Namen des Zusammenhangs auch dessen Voraussetzungen und Behauptungen sowie ggf. eine verallgemeinerte (ikonische oder symbolische) Darstellung des Zusammenhangs enthält.

  Tab. 7.2: Strukturierter Wissensspeicher zu Winkelsätzen, angelehnt an Steinhöfel et al. (1988, S. 69)

  Name des Satzes	Voraussetzung	Skizze	Behauptung
  Scheitelwinkelsatz	\(\alpha\) und \(\beta\) sind ein Scheitelwinkelpaar.	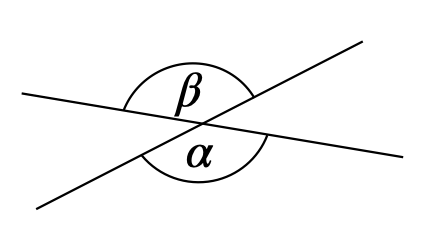	\(\alpha = \beta\)
  Nebenwinkelsatz	\(\alpha\) und \(\beta\) sind ein Nebenwinkelpaar.	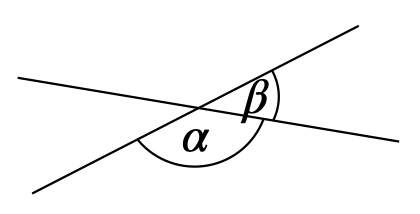	\(\alpha + \beta = 180°\)
  Stufenwinkelsatz	\(\alpha\) und \(\beta\) sind Stufenwinkel an geschnittenen Parallelen.	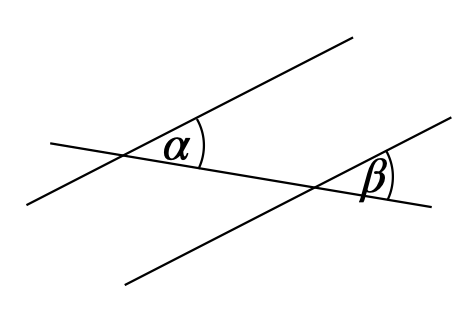	\(\alpha = \beta\)
  Wechselwinkelsatz	\(\alpha\) und \(\beta\) sind Wechselwinkel an geschnittenen Parallelen.	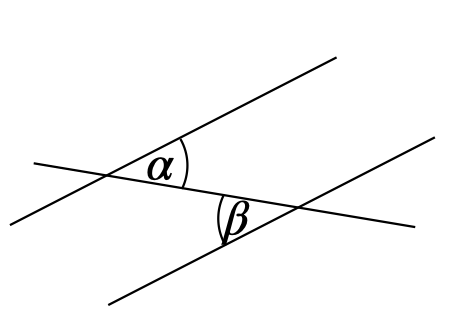	\(\alpha = \beta\)

• Ebenfalls der Betonung der inneren Struktur dienlich sind strukturbetonende Realisierungsmöglichkeiten. In diesen wird ein Zusammenhang dargestellt und die Darstellung dient gleichzeitig als »Ausfüllhilfe«. Solche Darstellungen mit Platzhaltern bieten sich insbesondere bei algebraischen Zusammenhängen an.

  Die erste binomische Formel lässt sich in der Form \(({\large\bigcirc} + \boxed{\phantom{X}})^2 = {\large\bigcirc}^2 + 2\cdot {\large\bigcirc}\cdot \boxed{\phantom{X}} + \boxed{\phantom{X}}^2\) darstellen, wobei die Kreise und Boxen mit entsprechenden Werten oder Variablen gefüllt werden können.

• Für das Finden einer Begründung kann folgende Handlungsvorschrift als Orientierungshilfe dienen (angelehnt an Steinhöfel et al., 1988, S. 72):

  1. Formulieren des Zusammenhangs als Wenn-dann-Aussage
  2. Feststellen von Voraussetzung und Behauptung
  3. Erstellen einer Überlegungsfigur, Bezeichnung wichtiger Teile sowie der Voraussetzung und Behauptung
  4. Überlegung, woraus die Behauptung folgen kann. Dabei Verwendung der Überlegungsfigur sowie Orientierung an
     • Definitionen vorkommender Begriffe
     • Sätzen mit gleicher Behauptung
     • Sätzen mit ähnlicher Behauptung
  5. Abwägung, welcher Satz bzw. welche Definition geeignet ist
  6. Nachweis der Behauptung aus den bei 5. gewählten Beweismitteln

• Für die Darstellung einer Begründung kann ein Beweisschema Orientierung bieten. So können bspw. Beweise in einer Tabelle dargestellt werden, bestehend aus einer Spalte zum Beweisschritt und einer zur zugehörigen Begründung. Dies ist insbesondere für direkte Beweise geeignet, bei denen von der Voraussetzung zur Behauptung geschlossen wird.

7.2.3 Zusammenhänge festigen

Zum Festigen von Zusammenhängen eignet sich nach Steinhöfel et al. (1988, S. 34) u. a. die Einschränkung einer oder mehrerer Voraussetzungen oder das Vertauschen von Voraussetzung und Behauptung, um die weitere Gültigkeit zu prüfen. Wie auch schon bei Begriffen sollten weiterhin Bezeichnungen variiert und alternative Formulierungen betrachtet werden. Auch bietet es sich an, Zusammenhänge mit gleicher oder ähnlicher Behauptung zu betrachten. Auch hier sei an die systematische Übersicht in Tabelle 7.3 verwiesen.

Nach Vollrath & Roth (2012, S. 49) ist ein Zusammenhang verstanden, wenn Schülerinnen und Schüler

• den Zusammenhang angemessen formulieren können,
  
• Beispiele für den Zusammenhang angeben können,
  
• wissen, unter welchen Voraussetzungen der Zusammenhang gilt,
  
• den Zusammenhang begründen können,
  
• Konsequenzen des Zusammenhangs kennen,
  
• Anwendungen des Zusammenhangs kennen.

7.3 Verfahren

Verfahren dienen in der Mathematik der Verallgemeinerung einer Lösung von einem spezifischen Problem hin zu einer ganzen Klasse von Problemen. Für die ausführenden Schülerinnen und Schüler verschiebt sich damit der (idealerweise) kreative Prozess bei der Behandlung von Begriffen und Zusammenhängen hin zu einem disziplinierten Arbeiten (vgl. Vollrath & Roth, 2012, 262 f.). Dabei darf das Verfahren jedoch nicht als geistig leeres Abarbeiten eines Lösungschemas verstanden werden, sondern auch die »Herkunft des Verfahrens« (z. B. Begründung einzelner Schritte) sind Bestandteil der Verfahrenskenntnisse.

Vollrath & Roth (2012, S. 261, Hervorhebungen im Original) zufolge beziehen sich Verfahren »in der Arithmetik in erster Linie auf die Rechenoperationen in den verschiedenen Zahlbereichen, auf das Lösen von Sachaufgaben für Größen mit Hilfe von Funktionen sowie auf die Bestimmung von Funktionswerten; in der Algebra betreffen sie das Lösen von Gleichungen, Gleichungssystemen und Ungleichungen; in der Geometrie geht es um das Konstruieren, das Berechnen von Umfängen, Flächeninhalten und Rauminhalten, das Darstellen von Körpern und in der Trigonometrie um die Dreiecksberechnungen.«

Dabei bauen Verfahren auf Begriffe und Zusammenhänge auf – benötigen i. d. R. sogar mehrere von ihnen. Diese müssen also sicher zur Verfügung stehen. Oftmals ist eine Hierarchie von Begriffen und Zusammenhängen bzw. vorheriger Verfahren nötig, um neue Verfahren aufzubauen (z. B. baut die schriftliche Multiplikation u. a. auf die schriftliche Addition und das kleine Einmaleins im Kopf auf, vgl. Vollrath & Roth, 2012, S. 262). Die Behandlung von Verfahren dient damit gleichzeitig auch der vertiefenden Aneignung von Begriffen und Zusammenhängen.

7.3.1 Verfahren gewinnen

Entsprechend ihrer Eigenschaft, dass Verfahren dem effektiven Lösen einer Klasse von Problemen dienlich sind, können Verfahren über eine reflektierende Betrachtung der Lösung spezifischer Probleme derselben Problemklasse erarbeitet werden. Geeignete Reflexionsfragen sind dabei:

• Was haben all die betrachteten Probleme gemeinsam?
• Welche Schritte haben wir jeweils durchgeführt, um das Problem zu lösen?
• Wozu haben wir die Schritte durchgeführt?
• Warum war es möglich, die Schritte durchzuführen?

Die letzten beiden Fragen beziehen sich auf das Ziel (»Wozu?«) und den Weg (»Warum?«) der jeweiligen Verfahrensschritte.²² Vollrath & Roth (2012, S. 264) stellen am Beispiel des Lösens der Gleichung \(5x = 10\) dar, dass eine Unterscheidung zwischen Ziel (»die \(5\) auf die andere Seite bekommen«) und Weg (durch \(5\) dividieren) bei der Verfahrensgewinnung hilfreich sein kann. Während das Ziel die Notwendigkeit des Schrittes begründet, nimmt der Weg Bezüge auf die im Hintergrund wirkenden Begriffe und Sachverhalte und liefert damit eine kausale Begründung für den Verfahrensschritt.

7.3.2 Verfahren aneignen

Die Aneignung eines Verfahrens erfolgt i. d. R. über dessen Anwendung. Im Sinne der etappenweisen Ausbildung bedeutet dies (Steinhöfel et al., 1988, S. 118):

• Auf der Etappe der materiellen/materialisierten Handlung liegt der Verfahrensablauf in schriftlicher Form vor.
• Auf der Etappe der sprachlichen Handlung liegt der Verfahrensablauf nicht mehr schriftlich vor. Die einzelnen Schritte werden von den Schülerinnen und Schülern während der Ausführung kommentiert.
• Auf der Etappe der geistigen Handlung führen die Schülerinnen und Schüler das Verfahren selbstständig und ohne schriftlich vorliegenden Verfahrensablauf aus.

Als Orientierungshilfe dient die schriftliche Fixierung des Verfahrensablaufs selbst – als Wortvorschrift, als Flussdiagramm bzw. als Graph o. Ä.

7.3.3 Verfahren festigen

Verfahren können u. a. gefestigt werden, indem einzelne im Verfahren auftretende Operanden spezialisiert werden (z. B. die beiden Summanden bei der schriftlichen Addition) – dies entspricht im Endeffekt einer Fallunterscheidung. Auch ist die Untersuchung unterschiedlicher Reihenfolgen der Verfahrensoperationen oder eine Variabilität der Darstellung des Verfahrens (z. B. Blockschema, Wortvorschrift, Graph, …) möglich. Weiterhin können Unter- bzw. Oberalgorithmen betrachtet, Umkehroperationen gebildet oder unterschiedliche Variablengrundbereiche untersucht werden (vgl. Steinhöfel et al., 1988, S. 34).

Nach Vollrath & Roth (2012, 49 f.) ist ein Verfahren verstanden, wenn Schülerinnen und Schüler

• wissen, was man damit erreicht,
  
• wissen, wie es geht,
  
• es auf Beispiele anwenden können,
  
• wissen, unter welchen Voraussetzungen es funktioniert,
  
• wissen, warum es funktioniert.

7.4 Zusammenfassung

In den letzten Abschnitten hat sich gezeigt, dass die Behandlung von Begriffen, Zusammenhängen und Verfahren grundsätzliche Ähnlichkeiten aufweisen. So konnten stets die Teilprozesse einer Erarbeitung (Begriffe bilden, Zusammenhänge und ihre Begründungen finden, Verfahren gewinnen), einer Aneignung (unter Zuhilfenahme von Orientierungshilfen mit dem Ziel der etappenweie Ausbildung geistiger Handlungen) und einer Festigung identifiziert werden. Für letztere zeigt Tabelle 7.3 noch einmal eine Gegenüberstellung von Möglichkeiten.

Tab. 7.3: Möglichkeiten zur Festigung von Begriffen, Zusammenhängen und Verfahren, nach Steinhöfel et al. (1988, S. 34)

	Begriffe	Zusammenhänge	Verfahren
Verwendung von Spezial- und Extremfällen	Unterbegriffe; Grenzfälle	Einschränkung einer oder mehrerer Voraussetzungen im Gültigkeitsbereich; Fallunterscheidungen	Spezialisierung von Operanden (Fallunterscheidungen)
Umformulieren	verschiedene Definitionsarten; Definition in Merkmalssystem verwandeln	verschiedene logisch gleichwertige Formulierungen	evtl. unterschiedliche Reihenfolge der Operationen
Verwendung unterschiedlicher Bezeichnungen	Merkmale nicht an feste Variablensymbole binden	Voraussetzungen und Behauptungen nicht an feste Symbole binden	unterschiedliche Formalisierungen (Blockschema, Wortvorschrift, Graph, …)
Bekanntes Neuem gegenüberstellen und Zusammenhänge erkennen lassen	Oberbegriffe; Einordnung in Begriffssystem	Sätze mit gleicher Behauptung; Sätze mit ähnlicher Behauptung	Unteralgorithmen; Oberalgorithmen
Umkehrungen bilden		Voraussetzungen und Behauptungen vertauschen	Umkehroperationen bilden
Bedingungen variieren	Merkmalsvariation durch Weglassen bzw. Hinzufügen von Merkmalen, Ändern der log. Verknüpfung	Weglassen bzw. Hinzufügen von Voraussetzungen	unterschiedliche Variablengrundbereiche

Weiterführende Möglichkeiten zur Erarbeitung von Begriffen, Zusammenhängen und Verfahren stellen Vollrath & Roth (2012, 227 ff.) dar.

7.5 Zum Nachbereiten

1. Beschreiben Sie für ein Verfahren aus der Sekundarstufe I unterrichtliche Möglichkeiten, dieses zu gewinnen.

2. Entwickeln Sie, entsprechend der Zusammenfassung in Tabelle 7.3, Festigungsaufgaben zum Begriff Erwartungswert, zum Zusammenhang Satz des Pythagoras oder zum Verfahren Polynomdivision.

References

Giest, H., & Lompscher, J. (2004). Tätigkeitstheoretische Überlegungen zu einer neuen Lernkultur. Sitzungsberichte der Leibniz-Sozietät, 72, 101–123. https://leibnizsozietaet.de/wp-content/uploads/2012/11/07_giest.pdf

Lompscher, J. (1996). Aufsteigen vom Abstrakten zum Konkreten - Lernen und Lehren in Zonen der nächsten Entwicklung. https://publishup.uni-potsdam.de/opus4-ubp/frontdoor/deliver/index/docId/444/file/AUFSTEIG.pdf

Rembowski, V. (2015). Eine semiotische und philosophisch-psychologische Perspektive auf Begriffsbildung im Geometrieunterricht. Begriffsfeld, Begriffsbild und Begriffskonvention und ihre Implikationen auf Grundvorstellungen [Dissertation, Universität des Saarlandes]. https://doi.org/10.22028/D291-26661

Steinhöfel, W., Reichold, K., & Frenzel, L. (1988). Zur Gestaltung typischer Unterrichtssituationen im Mathematikunterricht. Ministerium für Volksbildung.

Vollrath, H.-J., & Roth, J. (2012). Grundlagen des Mathematikunterrichts in der Sekundarstufe (F. Padberg, Hrsg.; 2. Aufl.). Spektrum Akademischer Verlag. https://doi.org/10.1007/978-3-8274-2855-4

Wikipedia. (2021b). Signifikant — Wikipedia, die freie Enzyklopädie. https://de.wikipedia.org/w/index.php?title=Signifikant&oldid=212433603

Wikipedia. (2021c). Signifikat — Wikipedia, die freie Enzyklopädie. https://de.wikipedia.org/w/index.php?title=Signifikat&oldid=214582005

Zech, F. (1998). Grundkurs Mathematikdidaktik (9. Aufl.). Beltz Verlag.

---

19. Diese Repräsentanten eines Begriffs sind nicht mit dessen Repräsentationen im Sinne der Grundvorstellungsidee zu verwechseln! Die Repräsentanten sind konkrete (reale oder ideelle) Objekte, Repräsentationen dagegen Darstellungen, die ein operatives Arbeiten ermöglichen. Beides kann aber natürlich sehr ähnlich aussehen oder sogar zusammenfallen.↩︎

20. Spezifischer sprechen einige Quellen auch von der Satzfindung, Beweisfindung und Beweisdarstellung, z. B. Steinhöfel et al. (1988, S. 59)↩︎

21. Eine Übersicht über Heurismen bietet bspw. die Webseite https://proffi-m.de/theorie.↩︎

22. Vollrath & Roth (2012, S. 264) verweisen hier auf die umgangssprachliche Vermischung der beiden Fragen »Wozu?« und »Warum?«.↩︎