2 (Hoch-)Schulmathematik strukturieren

Ziele

• Sie erkennen den Nutzen der Hochschulmathematik bei der Entscheidungsfindung zur Spezifizierung und Strukturierung der Schulmathematik auf der formalen Ebene des Vier-Ebenen-Ansatzes.
• Sie kennen geeignete Quellen zur Beantwortung der Fragen auf der formalen Ebene des Vier-Ebenen-Ansatz
  
• Sie kennen verschiedene Möglichkeiten, Mathematik zu strukturieren.
  
• Sie können beschreiben, woher die verschiedenen Strukturierungsmöglichkeiten kommen.

Material

• Folien zum Kapitel 2 (pdf, Keynote)

2.1 Allgemeine Hinweise

2.1.1 Doppelte Diskontinuität

Auf der formalen Ebene des Vier-Ebenene-Ansatzes soll der zu betrachtende Lerngegenstand fachmathematisch untersucht werden, um eine erste Auswahl (Spezifizierung) und Anordnung (Strukturierung) der Lerninhalte zu ermöglichen. Dies ruft natürlich – auch für Lerngegenstände der Grundschulmathematik – danach, die im Studium erworbenen hochschulmathematischen Erkenntnisse zu nutzen. Dieser Ruf wird jedoch (scheinbar!) geschmälert durch eine offensichtliche Ungleichheit zwischen Schulmathematik und Hochschulmathematik. Felix Klein beschreibt dieses Phänomen, das sich insbesondere auf die Ausbildung von Lehrkräften auswirkt, bereits im Übergang vom 19. zum 20. Jahrhunderts als doppelte Diskontinuität: »Der junge Student sieht sich am Beginn seines Studiums vor Probleme gestellt, die ihn in keinem Punkte mehr an die Dinge erinnern, mit denen er sich auf der Schule beschäftigt hat; natürlich vergißt er daher alle diese Sachen rasch und gründlich. Tritt er aber nach Absolvierung des Studiums ins Lehramt über, so soll er plötzlich eben diese herkömmliche Elementarmathematik schulmäßig unterrichten; da er diese Aufgabe kaum selbständig mit seiner Hochschulmathematik in Zusammenhang bringen kann, so wird er in den meisten Fällen recht bald die althergebrachte Unterrichtstradition aufnehmen, und das Hochschulstudium bleibt ihm nur eine mehr oder minder angenehme Erinnerung, die auf seinen Unterricht keinen Einfluß hat.« (Klein, 1967, S. 1)²

Einen Ausweg, dieser doppelten Diskontinität zu entgehen, sah Klein in einer Elementarmathematik vom höheren Standpunkte aus (Klein, 1925, 1955, 1967). Dabei verfolgt er »das Ziel, im Anschluss an umfassende hochschulmathematische Erfahrungen die Schulmathematik in den erworbenen Wissenskanon fachlich einzubetten« (Danckwerts, 2013, S. 78).

Diesen Gedanken fortsetzend kann man auch »gleich am Anfang des Studiums direkt und explizit an die schulmathematischen Vorerfahrungen an[knüpfen], bleibt inhaltlich bei diesen und arbeitet einen höheren Standpunkt heraus, der auf die vertiefte Auseinandersetzung mit der Oberstufenmathematik zielt und prinzipiell mit den bis dahin erworbenen (elementar-)mathematischen Mitteln auskommt.« (Danckwerts, 2013, S. 78) Eine solche Entwicklung hat das Projekt Mathematik Neu Denken verfolgt, das gut 100 Jahre nach Kleins Publikationen die Lehramtsausbildung im Fach Mathematik weiterentwickeln wollte (Beutelspacher et al., 2012). Entwickelt wird daraus eine Schulmathematik vom höheren Standpunkt, die auf eine fachliche und verstehensorientierte Durchdringung der Schulmathematik zielt, »ohne im vollen Umfang auf das Instrumentarium der kanonischen […] [Hochschulmathematik] zurückgreifen zu müssen« (Danckwerts, 2013, S. 87).

Im Rahmen der Stoffdidaktik-Veranstaltung sollen beide Ansätze aufgegriffen und an konkreten Beispielen versucht werden, die Fragen der formalen Ebene zu beantworten.

2.1.2 Geeignete Quellen

• Neben den Werken von Felix Klein zu Beginn des 20. Jahrhunderts (Klein, 1925, 1955, 1967) und aktuellen Ansätzen zum Umgang mit der doppelten Diskontinuität in der Lehramtsausbildung (Ableitinger et al., 2013; Beutelspacher et al., 2012) liefern die in den 1970er Jahren von Hans Freudenthal verfassten Werke zur Mathematik als pädagogische Aufgabe (Freudenthal, 1973c, 1973b; englischsprachig auch digital verfügbar über Freudenthal, 1973a) Ansätze, Schul- und Hochschulmathematik miteinander in Bezug zu bringen.

• Ebenfalls hilfreich sind größere Nachschlagewerke zur Mathematik, bspw. die Kleine Enzyklopädie Mathematik (Gellert et al., 1986).

• Nicht zu unterschätzen für die fachmathematische Auseinandersetzung sind auch fachdidaktische Quellen, insbesondere zur Didaktik der Sachgebiete. Als digital verfügbare Quellen seien zu erwähnen:

  • Didaktik der Algebra: nach der Vorlage von Hans-Joachim Vollrath (Weigand et al., 2022)
  • Didaktik der Geometrie für die Sekundarstufe I (Weigand et al., 2018)
  • Didaktik der Analysis. Aspekte und Grundvorstellungen zentraler Begriffe (Greefrath et al., 2016)
  • Didaktik der Stochastik in der Sekundarstufe I (Krüger et al., 2015)
  • Didaktik der Analytischen Geometrie und Linearen Algebra: Algebraisch verstehen – Geometrisch veranschaulichen und anwenden (Henn & Filler, 2015)
  • Mathematikunterricht in der Sekundarstufe II. Band 1: Fachdidaktische Grundfragen, Didaktik der Analysis (Tietze et al., 2000a)
  • Mathematikunterricht in der Sekundarstufe II. Band 2: Didaktik der Analytischen Geometrie und Linearen Algebra (Tietze et al., 2000b)
  • Mathematikunterricht in der Sekundarstufe II. Band 3: Didaktik der Stochastik (Tietze et al., 2002)

• Ebenfalls hilfreich für die fachliche Spezifizierung und Strukturierung kann die Darstellung der Fachinhalte in Schulbüchern sein. Hier bietet sich eine vergleichende Analyse mehrerer Schulbücher, auch unterschiedlicher Bundesländer, an.

• Nur gering geeignet für die Spezifizierung und Strukturierung sind die Bildungsstandstandards und Rahmenlehrpläne. Sie bieten – entsprechend ihrer Funktion – bereits eine Auswahl der zu unterrichtenden Inhalte und schränken damit die fachdidaktische Diskussion diesbezüglich ein.

Mathematik kann auf verschiedene Weisen strukturiert werden. Manche Strukturierungsmöglichkeiten orientieren sich stärker an der Fachwissenschaft (z. B. Sachgebiete), andere haben über die Gestaltung der Bildungsstandards eine eher politische Funktion (z. B. Litdeen). Im Folgenden werden drei Strukturierungsmöglichkeiten vorgestellt.

2.2 Sachgebiete

Für die Fachwissenschaft Mathematik haben sich historisch verschiedene Unterdisziplinen entwickelt, die als Sachgebiete der Mathematik bezeichnet werden können. Schulrelevante Gebiete sind hierbei:

• Arithemtik
• Algebra
• Geometrie
• Analysis
• Stochastik
• Lineare Algebra / Analytische Geometrie

Auch heute bilden sich diese und weitere Sachgebiete (z. B. Numerik) in den Strukturen von universitären Lehrveranstaltungen, Forschungsrichtungen und nicht zuletzt der Strukturierung einzelner Lehrpläne der Schulen ab.

Für eine Vertiefung mit der Didaktik der Sachgebiete eignen sich u. a. die in Abschnitt 2.1.2 dargestellten Quellen. Weiterhin werden Sie im Masterstudium im Modul Ausgewählte Themen der Mathematikdidaktik³ die Möglichkeit haben, sich mit der Didaktik einzelner Sachgebiete näher auseinanderzusetzen.

2.3 Leitideen

Die Strukturierung mathematischer Inhalte in Leitideen ist seit Anfang der 2000er Jahre im deutschen Bildungswesen etabliert, als die KMK⁴ Bildungsstandards für den Mittleren Schulabschluss (2004), den Primarbereich (2005) und später auch die Allgemeine Hochschulreife (2012) herausgebracht hat. Darauf aufbauend wurden in den meisten Bundesländern die Lehrpläne angepasst. Zwischenzeitlich wurden die Bildungsstandards für den Primarbereich sowie den Ersten und Mittleren Schulabschluss überarbeitet, für die gymnasiale Oberstufe gelten während der gerade laufenden Überarbeitung noch die von 2012. (Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, 2012, 2022b, 2022a). In Brandenburg spiegeln sich die Bildungsstandards in den Rahmenlehrplänen für die Jahrgangsstufen 1 – 10 und die Gymnasiale Oberstufe wider (Ministerium für Bildung, Jugend und Sport des Landes Brandenburg, 2022, 2023).

Im Laufe der letzten 20 Jahre haben sich für die Leitideen teils verschiedene Bezeichnungen ergeben. In den aktuellen Bildungsstandards des Ersten und Mittleren Schulabschlusses (Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, 2022a) werden verwendet:

• Leitidee Zahl und Operation
• Leitidee Größen und Messen
• Leitidee Strukturen und funktionaler Zusammenhang
• Leitidee Raum und Form
• Leitidee Daten und Zufall

Die Leitidee Zahl und Operation beispielweise »umfasst sinntragende Vorstellungen und Darstellungen von Zahlen und Operationen sowie die Nutzung von Rechengesetzen und Kontrollverfahren. Dazu gehören die sachgerechte Nutzung von Prozent- und Zinsrechnung ebenso wie kombinatorische Überlegungen und Verfahren, denen Algorithmen zu Grunde liegen.« (Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, 2022a, S. 15). Weiterhin werden diese Kompetenzen an spezifischen Fachinhalten konkretisiert, etwa: »Die Schülerinnen und Schüler […] • untersuchen Zahlen nach ihren Faktoren, in einfachen Fällen ohne digitale Mathematikwerkzeuge, • stellen Zahlen der Situation angemessen dar, z.B. unter anderem in Zehnerpotenzschreibweise, • rechnen mit natürlichen, ganzen und rationalen Zahlen, die im täglichen Leben vorkommen, sowohl zur Kontrolle als auch im Kopf und erklären die Bedeutung der Rechenoperationen […]« (Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, 2022a, S. 15)

Die konkreten Ausführungen innerhalb der Leitideen werden in den Bildungsstandards als inhaltsbezogene Kompetenzen beschrieben, die mit Abschluss des ersten bzw. mittleren Schulabschlusses zu erreichen sind. Es handelt sich dabei um Regelstandards, also Kompetenzen, die »Schülerinnen und Schüler im Durchschnitt in einem Fach erreichen sollen« (Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, 2022a, S. 2). Diese sind abzugrenzen gegenüber Basiskompetenzen als »mathematisch zentrale, instrumentell bedeutsame und geradezu grundlegende Konzepte und Verfahren, die für die mathematische Kompetenzentwicklung unverzichtbar sind« (vgl. https://pikas-mi.dzlm.de/node/92). Für Basiskompetenzen gibt es derzeit in Deutschland keine politischen Dokumente wie Rahmenlehrpläne oder Bildungsstandards.

2.4 Stoffelementkategorien

Eine weitere Strukturierung mathematischen Wissens kann darin bestehen, den Blick darauf zu lenken, wie dieses Wissen angeeignet wird. So können ähnliche Aneigungsprozesse Motivation bieten, das Wissen entsprechend zu strukturieren und dies dann für die Gestaltung von Lehr-Lern-Prozessen nutzbar zu machen. Die Bezeichnung Stoffelementkategorie nutzt u. a. Zais (2003), während Vollrath & Roth (2012, 45 f.) von Arten mathematischen Wissens sprechen. Es können drei Kategorien unterschieden werden.

• Begriffe. Diese bilden das Grundgerüst der Mathematik und belegen Objekte gleicher Eigenschaft mit einem gemeinsamen Bezeichner. Neben der Begriffsfestlegung, i. d. R. über eine Definition, ist der Einsatz geeignter Beispiele und Gegenbeispiele essentiell beim Aufbau eines Begriffsverständnisses.

• Zusammenhänge. Diese beschreiben Eigenschaften von Begriffen und ihre Beziehungen zueinander. Klassischerweise gehören hierzu mathematische Sätze inkl. ihrer Beweise, aber auch präformale Begründungen. Bei Vollrath & Roth (2012, 45 f.) wird statt von Zusammenhängen von Sachverhalten gesprochen, ältere Quellen beziehen sich auch nur auf Sätze.

• Verfahren. Diese bestimmen, wie bestimmte Aufgaben zu lösen sind, z. B. schriftliche Rechenverfahren, Lösungsverfahren von Gleichungen und Gleichungssystemen.

Einige Autoren zählen zu den Verfahren auch heuristische Strategien zum Problemlösen oder die Anwendung des Permanenzprinzips (vgl. Steinhöfel et al., 1988, S. 23). Vollrath & Roth (2012, S. 46 ff.) ergänzen inhaltlich ähnlich:

• Metamathematisches Wissen. Darunter ist zu verstehen, wie Mathematik betrieben wird, also bspw. welche Möglichkeiten es gibt, ein mathematisches Problem zu lösen oder eine Sachsituation mathematisch zu modellieren.

In den nächsten Kapiteln wird näher darauf eingegangen, wie Lernprozesse bei der Ausbildung der jeweiligen Stoffelement-Kategorien gestaltet werden können.

2.5 Beispiel Negative Zahlen

Am Beispiel der negativen Zahlen soll dargestellt werden, wie eine Sichtweise vom höheren Standpunkt auf die in der Schule relevante Behandlung dieses Lerngegenstands zur Spezifizierung und Strukturierung helfen kann. Dabei beinhalten die negativen Zahlen sowohl die ganzen Zahlen als auch die rationalen Zahlen.

2.5.1 Natürliche Zahlen

Fachmathematisch können die ganzen Zahlen aus den natürlichen Zahlen generiert werden. Hierzu sollen zunächst die natürlichen Zahlen selbst fachmathematisch eingeordnet werden. Im Prinzip bestehen zwei Sichtweisen, nämlich die Einführung über die Peano-Axiome sowie die Betrachtung gleichmächtiger Mengen.

Aus den Peano-Axiomen (Wikipedia, 2021a) folgt zunächst die Existenz einer Reihenfolge von Zahlen (also Nachfolger der \(0\)), die dann mit \(1\), \(2\), \(3\) usw. bezeichnet werden können.⁵ Diese Bezeichnung erlaubt jedoch noch keinerlei Berechnungen, nicht einmal eine Ordnungsrelation ist vorhanden. Es kann also (noch) nicht gesagt werden, dass \(3\) größer ist als \(1\). Vielmehr lässt sich die Situation eher mit einem Alphabet vergleichen⁶, bei dem auch nicht C größer als A ist.

Für eine Ordnungsrelation bedarf es zunächst der Definition der Addition über \(n+0 := n\) und \(n+k' := (n+k)'\) für alle \(n,k\in\mathbb{N}\) mit der (aus den Peano-Axiomen existierenden) Nachfolgerbildung \('\). So gilt etwa mit \(1:=0'\): \({\color{blue} 1}+{\color{red} 1} = {\color{blue} 1}+{\color{red} {0'}} = ({\color{blue} 1}+{\color{red} 0}){\color{red} '} = 1{\color{red} '} =: 2\). So kann nun induktiv jede höhere Additionsaufgabe generiert werden. Darauf aufbauend kann die Ordnungsrelation \(n<m\) über die Existenz eines \(k\in\mathbb{N}\backslash\{0\}\) mit \(m = n+k\) definiert werden. Die Subtraktion \(m-n = k\) ist nun wiederum über die Umkehroperation \(n+k = m\) definierbar, sofern \(m\geq n\).

Die Gleichmächtigkeit (z. B. endlicher) Mengen \(M\) und \(N\) wird über die Existenz einer Bijektion zwischen diesen beiden Mengen definiert, siehe Abbildung 2.1.

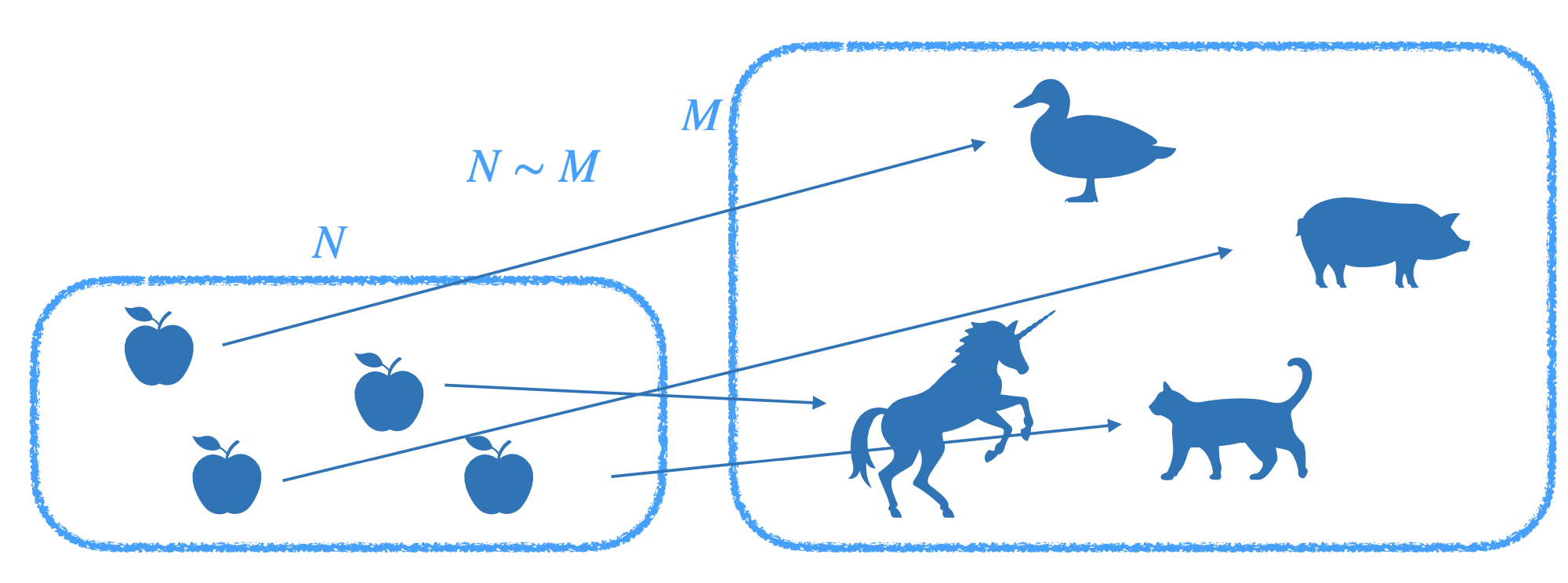
Abb. 2.1: Gleichmächtigkeit von Mengen

Diese Relation ist eine Äquivalenzrelation, also symmetrisch, reflexiv und transitiv. Damit können Äquivalenzklassen gebildet werden, die die Mächtigkeit der Menge angeben. \(4\) ist dann der Bezeichner für die Äquivalenzklasse von vierelementigen Mengen. Die Addition \(n+k\) entspricht dann der Mächtigkeit der Vereinigungsmenge von Mengen mit den Mächtigkeiten \(n\) und \(k\), vgl. Abbildung 2.2.

Abb. 2.2: Additionsergebnis als Äquivalenzklasse der Vereinigungsmenge

2.5.2 Ganze Zahlen

Da innerhalb der natürlichen Zahlen noch nicht beliebig subtrahiert werden darf, stehen auch keine negativen Zahlen als Ergebnisse zur Verfügung. Um dennoch das Ergebnis bspw. der Aufgabe \(2-7\) »definieren« zu können, bietet sich erneut eine Äquivalenzrelation über die »Differenzengleichheit« an. Konkret lässt sich für \(k,l,m,n\in\mathbb{N}\) sagen: \((k,l)\sim (m,n):\Leftrightarrow k+n=l+m\) Das heißt z. B., dass die Zahlenpaare \((2,7)\), \((0,5)\) und \((4,9)\) in Relation zueinander stehen, weil sie dieselbe »Differenz« haben (obwohl es die Differenz formal noch nicht gibt). Dies ermöglicht nun die Einführung des Bezeichners \(-5\) für die Äquivalenzklasse \([(0,5)]\).

Das Vorgehen ist verträglich mit den bisherigen Regeln in \(\mathbb{N}\), d. h. es führt nicht zu Widersprüchen, wenn etwa das Zahlenpaar \((7,4)\) betrachtet wird mit dem Repräsentanten-Bezeichner \(3\). Die Menge aller Äquivalenzklassen (bzw. deren Kurzbezeichner) ist nun \(\mathbb{Z}\).

Die Addition und Subtraktion zweier Zahlenpaare sind nun definierbar:

\[\begin{align} (k, l) + (m, n) := (k + m, l + n)\\ (k, l) − (m, n) := (k, l) + (n, m) \end{align}\]

Als Alternative bietet sich ein axiomatisches Vorgehen an, also dass die ganzen Zahlen mit der Addition als abelsche Gruppe definiert werden – bedeutsam ist hier insbesondere die Existenz eines Inversen zu jeder Zahl.

2.5.2.1 Permanenzprinzip und Permanenzreihen

Wie bereits erwähnt, führen die neu eingeführte Addition und Subtraktion in \(\mathbb{Z}\) nicht zu Konflikten mit den bisherigen analogen Operationen in \(\mathbb{N}\). Dies wird über das Permanenzprinzip gefordert, nach dem neue Theorien (z. B. das Rechnen mit negativen Zahlen) soweit wie möglich verträglich sein müssen mit bisherigen Theorien (z. B. das Rechnen mit positiven Zahlen).

Sichtbar gemacht werden kann dieses Prinzip über Permanenzreihen. Dies ist insbesondere dann hilfreich, wenn für bestimmte Rechenoperationen keine geeigneten realen Veranschaulichungen existieren. Ein typisches Beispiel hierfür ist die Multiplikation zweier negativer Zahlen. Kann die Multiplikation einer natürlichen Zahl (erster Summand) mit einer negativen Zahl (zweiter Summand) außermathematisch noch als mehrfache Verschuldung aufgefasst und die Vertauschung von erstem und zweitem Summanden über das Kommutativgesetz innermathematisch erklärt werden, bietet die Multiplikation zweier negativer Zahlen keine so naheliegende Interpretation. Abbildung 2.3 stellt eine Permanenzreihe dar, anhand derer die Rechnung \((-3)\cdot (-5)\) erklärt werden kann.

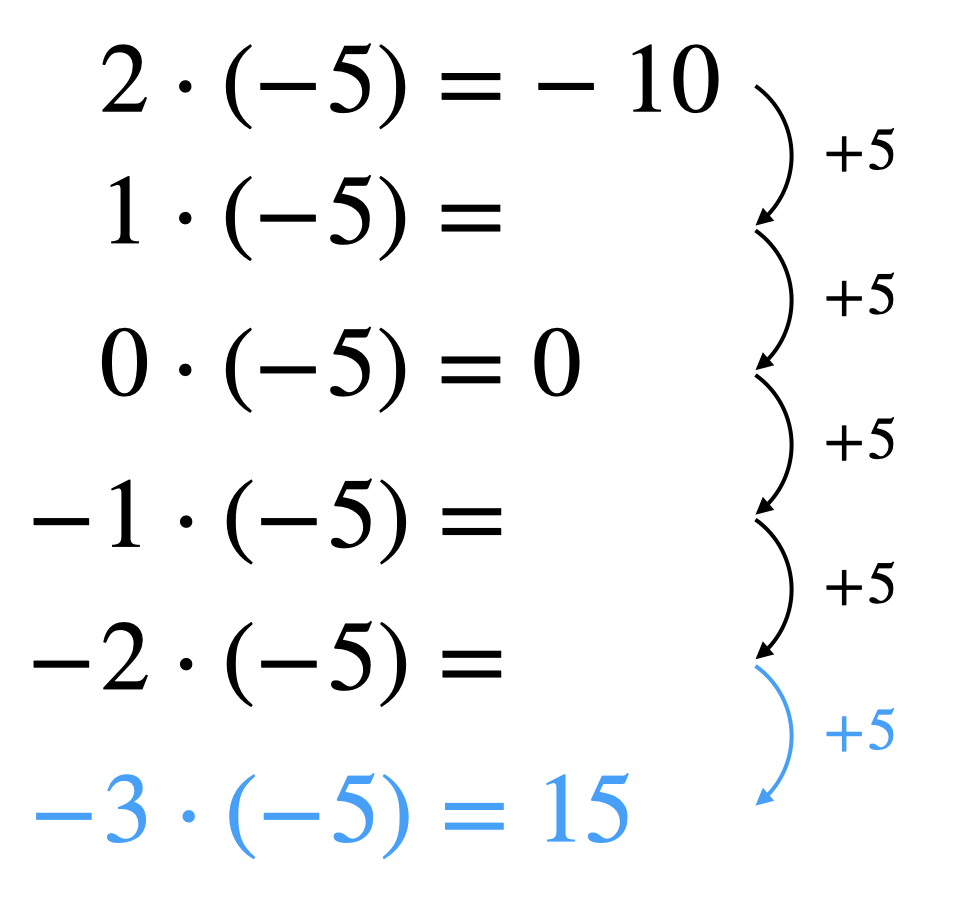
Abb. 2.3: Permanenzreihe zur Multiplikation zweier negativer Zahlen

Entscheidend ist beim Aufstellen von Permanenzreihen jedoch, dass der Übergang von einer Zeile zur nächsten auf einem entsprechenden Rechengesetz beruht. In Abbildung 2.3 ist dies das Distributivgesetz \((a-1) \cdot b = a \cdot b - b\). Vernachlässigt man die Existenz einer Übergangsregel, lassen sich plausibel erscheinende Muster fortsetzen (wie \(0^3 = 0\), \(0^2 = 0\), \(0^1 = 0\)), die dann allerdings zu falschen Schlussfolgerungen (\(0^0 = 0\)) führen. Im dargestellten Beispiel kann die Übergangsregel \(a^{m-1} = a^m : a\) wegen \(a = 0\) nicht angewandt werden.

Weitere Hinweise zum Einsatz des Permanenzprinzips im Mathematikunterricht finden Sie zum Beispiel bei Hoffkamp & Lensing (2024).

2.5.2.2 Ableitungen für den Lernpfad

Aus all den bisherigen Überlegungen auf der formalen Ebene lassen sich für den Unterricht zentrale Fachinhalte ableiten:

Ganze Zahlen können über Zahlenpaare aus den natürlichen Zahlen oder als »Gegenzahlen« der natürlichen Zahlen entwickelt werden.

• Natürliche Zahlen sind als Teilmenge in die ganzen Zahlen eingebettet.
• Die Subtraktion natürlicher Zahlen \(m-n\) mit \(n > m\) ist nun lösbar.
• Die Rechenregeln werden erweitert, wobei die bekannten weiter gelten. Die wird über das Permanenzprinzip begleitet, bei der Herleitung von Rechenregeln bietet sich die Nutzung von Permanenzreihen an.

2.5.3 Rationale Zahlen

In fachlich analoger Weise lassen sich auch die rationalen Zahlen über Äquivalenzrelationen einführen. Dann fordert die »Quotientengleichheit«, dass für \(k,l,m,n\in\mathbb{N}\) mit \(l,n\neq 0\) gilt: \((k,l)\sim (m,n):\Leftrightarrow k\cdot n=l\cdot m\). Die Äquivalenzklasse \([(1,2)]\) kann dann mit \(\frac{1}{2}\) bezeichnet werden. Im Gegensatz zu den ganzen Zahlen ist es bei den rationalen Zahlen durchaus üblich, für dieselbe Zahl unterschiedliche Bezeichner zu verwenden, wie \(\frac{1}{2}\) oder \(\frac{5}{10}\). Fachmathematisch ist dies jedoch nicht relevant, also auch keine Diskussion auf der formalen Ebene (jedoch auf späteren Ebenen).

Aus Sicht der formalen Ebene lässt sich daher auch nicht ableiten, ob im Mathematikunterricht nach den natürlichen Zahlen zunächst die rationalen Zahlen (wie z. B. in Deutschland) oder erst die ganzen Zahlen (wie z. B. in Australien) eingeführt werden sollten. Innerhalb eines Zahlbereichs bietet jedoch die fachlogische Struktur Ansatzpunkte zur Gestaltung des Lernpfads, wie bei den negativen Zahlen dargestellt.

References

Ableitinger, C., Kramer, J., & Prediger, S. (Hrsg.). (2013). Zur doppelten Diskontinuität in der Gymnasiallehrerbildung: Ansätze zu Verknüpfungen der fachinhaltlichen Ausbildung mit schulischen Vorerfahrungen und Erfordernissen. Springer Fachmedien Wiesbaden. https://doi.org/10.1007/978-3-658-01360-8

Beutelspacher, A., Danckwerts, R., Nickel, G., Spies, S., & Wickel, G. (2012). Mathematik Neu Denken. Vieweg+Teubner Verlag. https://doi.org/10.1007/978-3-8348-8250-9

Danckwerts, R. (2013). Angehende Gymnasiallehrer(innen) brauchen eine „Schulmathematik vom höheren Standpunkt“! In C. Ableitinger, J. Kramer, & S. Prediger (Hrsg.), Zur doppelten Diskontinuität in der Gymnasiallehrerbildung (S. 77–94). Springer Fachmedien Wiesbaden. https://doi.org/10.1007/978-3-658-01360-8_5

Freudenthal, H. (1973a). Mathematics as an Educational Task. Springer Netherlands. https://doi.org/10.1007/978-94-010-2903-2

Freudenthal, H. (1973c). Mathematik als pädagogische Aufgabe (Bd. 1). Klett.

Freudenthal, H. (1973b). Mathematik als pädagogische Aufgabe (Bd. 2). Klett.

Gellert, W., Küstner, H., Hellwich, M., Kästner, H., & Reichardt, H. (Hrsg.). (1986). Kleine Enzyklopädie Mathematik (13. Aufl.). VEB Bibliographisches Institut.

Greefrath, G., Oldenburg, R., Siller, H.-S., Ulm, V., & Weigand, H.-G. (2016). Didaktik der Analysis. Aspekte und Grundvorstellungen zentraler Begriffe (F. Padberg & A. Büchter, Hrsg.; 4. Aufl.). Springer Spektrum. https://doi.org/10.1007/978-3-662-48877-5

Henn, H.-W., & Filler, A. (2015). Didaktik der Analytischen Geometrie und Linearen Algebra: Algebraisch verstehen – Geometrisch veranschaulichen und anwenden. Springer Spektrum.

Hoffkamp, A., & Lensing, F. (Hrsg.). (2024). mathematik lehren 246: Permanenzprinzip. Friedrich Verlag.

Klein, F. (1925). Elementarmathematik vom Höheren Standpunkte aus II. Geometrie. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-642-90852-1

Klein, F. (1955). Elementarmathematik vom Höheren Standpunkte aus III. Präzisions- und Approximationsmathematik (C. H. Müller, Hrsg.). Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-00246-9

Klein, F. (1967). Elementarmathematik vom Höheren Standpunkte aus I. Arithmetik, Algebra, Analysis. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-11652-4

Krüger, K., Sill, H.-D., & Sikora, C. (2015). Didaktik der Stochastik in der Sekundarstufe I. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-43355-3

Ministerium für Bildung, Jugend und Sport des Landes Brandenburg (Hrsg.). (2022). Rahmenlehrplan für die gymnasiale Oberstufe. Teil C. Mathematik. https://bildungsserver.berlin-brandenburg.de/fileadmin/bbb/unterricht/rahmenlehrplaene/gymnasiale_oberstufe/curricula/2022/Teil_C_RLP_GOST_2022_Mathematik.pdf

Ministerium für Bildung, Jugend und Sport des Landes Brandenburg (Hrsg.). (2023). Rahmenlehrplan Brandenburg. Teil C, Mathematik, Jahrgangsstufen 1 – 10. https://bildungsserver.berlin-brandenburg.de/fileadmin/bbb/unterricht/rahmenlehrplaene/Rahmenlehrplanprojekt/amtliche_Fassung/getrennt_2023/BB_RLP_2023_Teil_C_Ma_GenF_1.pdf

Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland. (2012). Bildungsstandards im Fach Mathematik für die Allgemeine Hochschulreife. (Beschluss der Kultusministerkonferenz vom 18.10.2012). https://www.kmk.org/fileadmin/Dateien/veroeffentlichungen_beschluesse/2012/2012_10_18-Bildungsstandards-Mathe-Abi.pdf

Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland. (2022a). Bildungsstandards für das Fach Mathematik Erster Schulabschluss (ESA) und Mittlerer Schulabschluss (MSA). (Beschluss der Kultusministerkonferenz vom 15.10.2004 und vom 04.12.2003, i.d.F. vom 23.06.2022). https://www.kmk.org/fileadmin/Dateien/veroeffentlichungen_beschluesse/2022/2022_06_23-Bista-ESA-MSA-Mathe.pdf

Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland. (2022b). Bildungsstandards für das Fach Mathematik Primarbereich. (Beschluss der Kultusministerkonferenz vom 15.10.2004, i.d.F. vom 23.06.2022). https://www.kmk.org/fileadmin/Dateien/veroeffentlichungen_beschluesse/2022/2022_06_23-Bista-Primarbereich-Mathe.pdf

Steinhöfel, W., Reichold, K., & Frenzel, L. (1988). Zur Gestaltung typischer Unterrichtssituationen im Mathematikunterricht. Ministerium für Volksbildung.

Tietze, U.-P., Klika, M., & Wolpers, H. (Hrsg.). (2000a). Mathematikunterricht in der Sekundarstufe II. Band 1: Fachdidaktische Grundfragen, Didaktik der Analysis (2. Aufl.). Vieweg+Teubner Verlag. https://doi.org/10.1007/978-3-322-90568-0

Tietze, U.-P., Klika, M., & Wolpers, H. (Hrsg.). (2000b). Mathematikunterricht in der Sekundarstufe II. Band 2: Didaktik der Analytischen Geometrie und Linearen Algebra. Vieweg+Teubner Verlag. https://doi.org/10.1007/978-3-322-86479-6

Tietze, U.-P., Klika, M., & Wolpers, H. (Hrsg.). (2002). Mathematikunterricht in der Sekundarstufe II. Band 3: Didaktik der Stochastik. Vieweg+Teubner Verlag. https://doi.org/10.1007/978-3-322-83144-6

Vollrath, H.-J., & Roth, J. (2012). Grundlagen des Mathematikunterrichts in der Sekundarstufe (F. Padberg, Hrsg.; 2. Aufl.). Spektrum Akademischer Verlag. https://doi.org/10.1007/978-3-8274-2855-4

Weigand, H.-G., Filler, A., Hölzl, R., Kuntze, S., Ludwig, M., Roth, J., Schmidt-Thieme, B., & Wittmann, G. (2018). Didaktik der Geometrie für die Sekundarstufe I. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-56217-8

Weigand, H.-G., Schüler-Meyer, A., & Pinkernell, G. (2022). Didaktik der Algebra: nach der Vorlage von Hans-Joachim Vollrath. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-64660-1

Wikipedia. (2021a). Peano-Axiome — Wikipedia, die freie Enzyklopädie. https://de.wikipedia.org/w/index.php?title=Peano-Axiome&oldid=216675163

Wikipedia. (2022b). Kultusministerkonferenz — Wikipedia, die freie Enzyklopädie. https://de.wikipedia.org/w/index.php?title=Kultusministerkonferenz&oldid=228417777

Zais, T. (2003). Der Beitrag des Wissenschaftsbereichs "Methodik des Mathematikunterrichts" der Universität Karl-Marx-Stadt zur mathematikmethodischen Theoriebildung in der DDR. In H. Henning & P. Bender (Hrsg.), Didaktik der Mathematik in den alten Bundesländern — Methodik des Mathematikunterrichts in der DDR. Bericht über eine Doppeltagung zur gemeinsamen Aufarbeitung einer getrennten Geschichte (S. 246–256). http://www.math.uni-magdeburg.de/private/henning/tagung.pdf

---

2. Es handelt sich hier um den Nachdruck eines Werkes, dessen erste Auflage 1908 erschien.↩︎

3. siehe Modulbeschreibung zum Modul MAT-LS-D3 bei PULS↩︎

4. Mehr zur Kultusministerkonferenz (KMK) und ihrer eigentlichen Bezeichnungen siehe Wikipedia (2022b).↩︎

5. Ab 10 wird bei der Bezeichnung jedoch das Stellenwertsystem genutzt – das geht schon weiter als hier zulässig.↩︎

6. Ein wesentlicher Unterschied dieses Vergleiches ist, dass das Alphabet endlich ist, die Menge der natürlichen Zahlen jedoch nicht.↩︎