11 Geometrie
Ziele
- Sie sind sich der Verbindungen von Geometrie, Linearer Algebra und Analytischer Geometrie bewusst.
- Sie kennen enaktive, ikonische und symbolische Herangehensweisen zur Behandlung von Lagebeziehungen.
- Sie kennen Besonderheiten im Einsatz von DGS bei der Behandlung geometrischer Fragestellungen (wie Zugstabilität, Spuren und Ortslinien).
Material
Literaturempfehlungen
- Weigand et al. (2018): Didaktik der Geometrie für die Sekundarstufe I
- Henn & Filler (2015): Didaktik der Analytischen Geometrie und Linearen Algebra: Algebraisch verstehen – Geometrisch veranschaulichen und anwenden
- Tietze et al. (2000b): Mathematikunterricht in der Sekundarstufe II. Band 2: Didaktik der Analytischen Geometrie und Linearen Algebra
Der Geometrieunterricht der Sekundarstufe I ist geprägt von Begriffen, Zusammenhängen und Verfahren der Elementargeometrie. So werden geometrische Objekte (wie Punkte, Geraden, Winkel) und ihre Relationen betrachtet sowie Messungen (Längen, Flächeninhalte, Volumina, …) vorgenommen. Außerdem werden elementargeometrische Sätze (z. B. Satz des Thales, Satz des Pythagoras, Sinus- und Kosinussatz) behandelt. In Hinblick auf die Sekundarstufe II kommt es zur Koordinatisierung der geometrischen Objekte, üblicherweise über die Beschreibung in einem kartesischen Koordinatensystem. Liegen die geometrischen Objekte nun koordinatisiert vor, kann mit ihne in der Analytischen Geometrie »gerechnet« werden. Für die dazu anwendbaren Gesetzmäßigkeiten bedient man sich der Linearen Algebra, in der die zugrundeliegenden Strukturen veroretet sind.
Am Beispiel des Vektorbegriffs kann man sagen: Elementargeometrisch beschreibt ein Vektor eine Verschiebung in eine bestimmte Richtung um einen bestimmten Betrag. Koordinatisiert lässt sich der Vektor in der Analytischen Geometrie über ein Tupel beschreiben. Mit solchen Tupeln kann dann gerechnet werden, wobei entsprechende Gesetzmäßigkeiten (Vektoraddition, Skalierung) der Linearen Algebra entstammen, wo Vektoren als Elemente eines Vektorraums aufgefasst werden.
11.1 Lagebeziehungen
Lagebeziehungen zwischen Punkten, Geraden und Ebenen spielen über die gesamte Schullaufbahn eine bedeutsame Rolle. Es beginnt in der Grundschule über die Lage von Punkten auf Geraden, zueinander senkrechte und parallele Geraden, den Winkelbegriff zu Beginn der Sekundarstufe, bis hin zur Analytischen Geometrie in der Sekundarstufe II, wenn die Lagebeziehungen algebraisch beschrieben werden.
11.1.1 Lagebeziehungen falten
Werden auf einem Blatt Papier zwei Punkte markiert und diese aufeinandergefaltet, entsteht als Faltlinie die Mittelsenkrechte zwischen diesen beiden Punkten (siehe Abbildung 11.1).
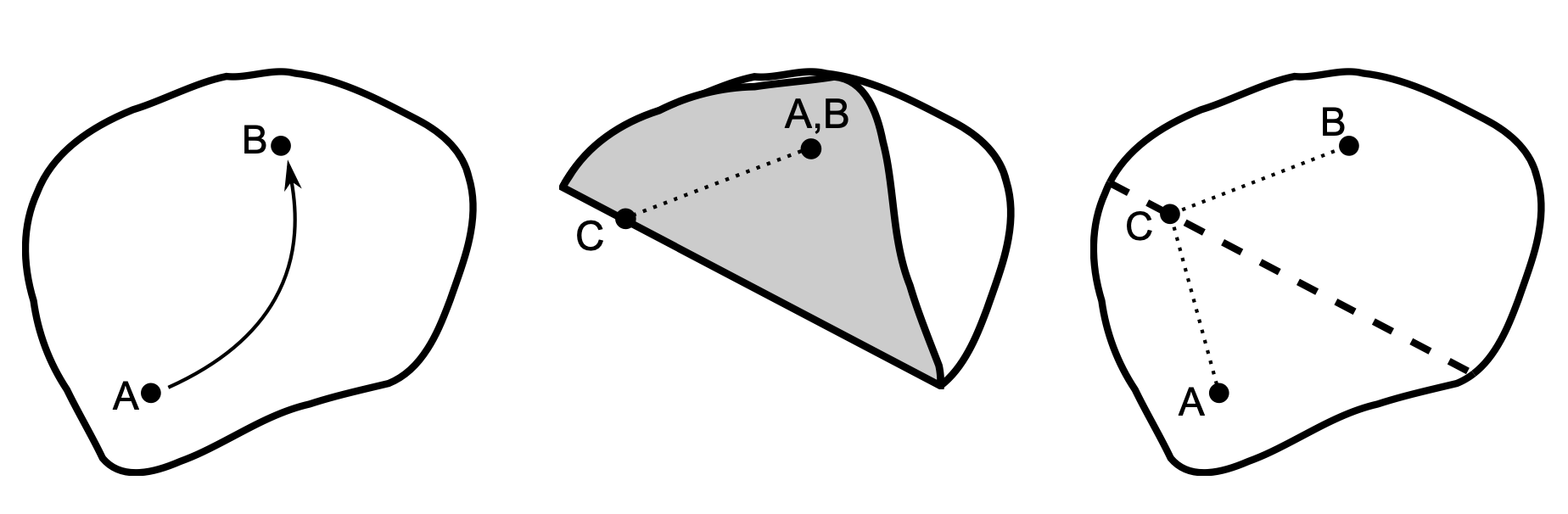
Abb. 11.1: Mittelsenkrechte durch Faltung (Etzold & Petzschler, 2014, S. 5)
Um dies zu begründen, muss die Faltung analysiert und mit der geometrischen Konfiguration in Zusammenhang gebracht werden. Betrachtet man einen Punkt \(C\) auf der Faltlinie, so hat dieser zu \(A\) und \(B\) denselben Abstand, was aus dem Übereinanderlegen von \(A\) und \(B\) durch die Faltung bekommt. Die Faltlinie ist damit die Menge aller Punkte (in der Ebene des Papierstücks), die zu \(A\) und \(B\) denselben Abstand haben – und dies ist gerade die Mittelsenkrechte.
Lerntheoretisch kann als Lernhandlung das Erkennen (als mehrfaches Identifizieren und Realisieren) der geometrischen Konfiguration der Faltung aufgefasst werden (vgl. typische Lernhandlungen im Mathematikunterricht in Abschnitt 5.1). Die Analyse dieser Lernhandlungen unterstützt nun die Aneignung geometrischen Wissens.
Fachdidaktisch interessant ist hier die Betonung der Ortslinieneigenschaft der Mittelsenkrechten. Diese Abstandsbedingung zu zwei Punkten ist auch relevant, um die Konstruktion einer Mittelsenkrechten durchzuführen – also das Zeichnen zweier Kreisbögen mit demselben Radius von den Punkten ausgehend, die Schnittpunkte liegen dann auf der Mittelsenkrechten. Auch wenn begründet werden soll, dass sich die Mittelsenkrechten der Seiten eines Dreiecks im Umkreismittelpunkt schneiden, bedarf es dieser Eigenschaft. Aus dem Bezeichner Mittelsenkrechte ist die entsprechende Eigenschaft dagegen nicht direkt ablesbar – handelt es sich demnach doch »nur« um eine Gerade, die senkrecht zur Strecke \(\overline{AB}\) und durch deren Mitte verläuft.39
Der Faltprozess kann also eine Motivation bieten, über eine zunächst enaktive Handlung die geometrische Eigenschaft der Faltprodukte genauer zu betrachten und die Faltung selbst »auseinanderzunehmen«. Ein solcher Analyseprozess kann nochmal verstärkt gefordert werden, wenn bspw. das Faltergebnis in einer Dynamischen Geometriesoftware (DGS) realisiert wird. Dann nämlich ist es notwendig, die Faltlinie über die im DGS zur Verfügung stehenden Werkzeuge zu realisieren (vgl. Etzold & Petzschler, 2014, S. 6).
In analoger Weise zur Faltung der Mittelsenkrechten durch Punkt-auf-Punkt-Faltung kann auch das Falten einer Winkelhalbierenden durch Kante-auf-Kante-Faltung realisiert werden. Darauf aufbauend wiederum können Senkrechten, Parallelen oder sogar Quadrate bzw. Kreismittelpunkte gefaltet werden (siehe Etzold & Petzschler, 2014, 10, 82 f., 86 f.).
11.1.2 Skalarprodukt
Zur Beschreibung von Lagebeziehungen zweier Geraden, insbesondere der Bestimmung des Winkels dazwischen, wird in der Sekundarstufe II das Skalarprodukt behandelt. Nach Henn & Filler (2015, S. 195 ff.) bestehen hierfür prinzipiell drei Zugänge:
- Bei einem geometrischen Zugang dient, wie bereits motiviert, die Winkelbestimmung als Anlass, das Skalarprodukt zu behandeln. Mit der Definition \(\left<\vec u, \vec v\right> := |\vec u|\cdot |\vec v|\cdot \cos(\angle(\vec u,\vec v))\) kann das Skalarprodukt interpretiert werden, indem einer der beiden Vektoren auf die Richtung des anderen Vektors projiziert wird und anschließend das Produkt gebildet wird. Letzteres ist als (gerichteter) Flächeninhalt des entsprechenden Rechtecks interpretierbar, vgl. Abbildung 11.2.
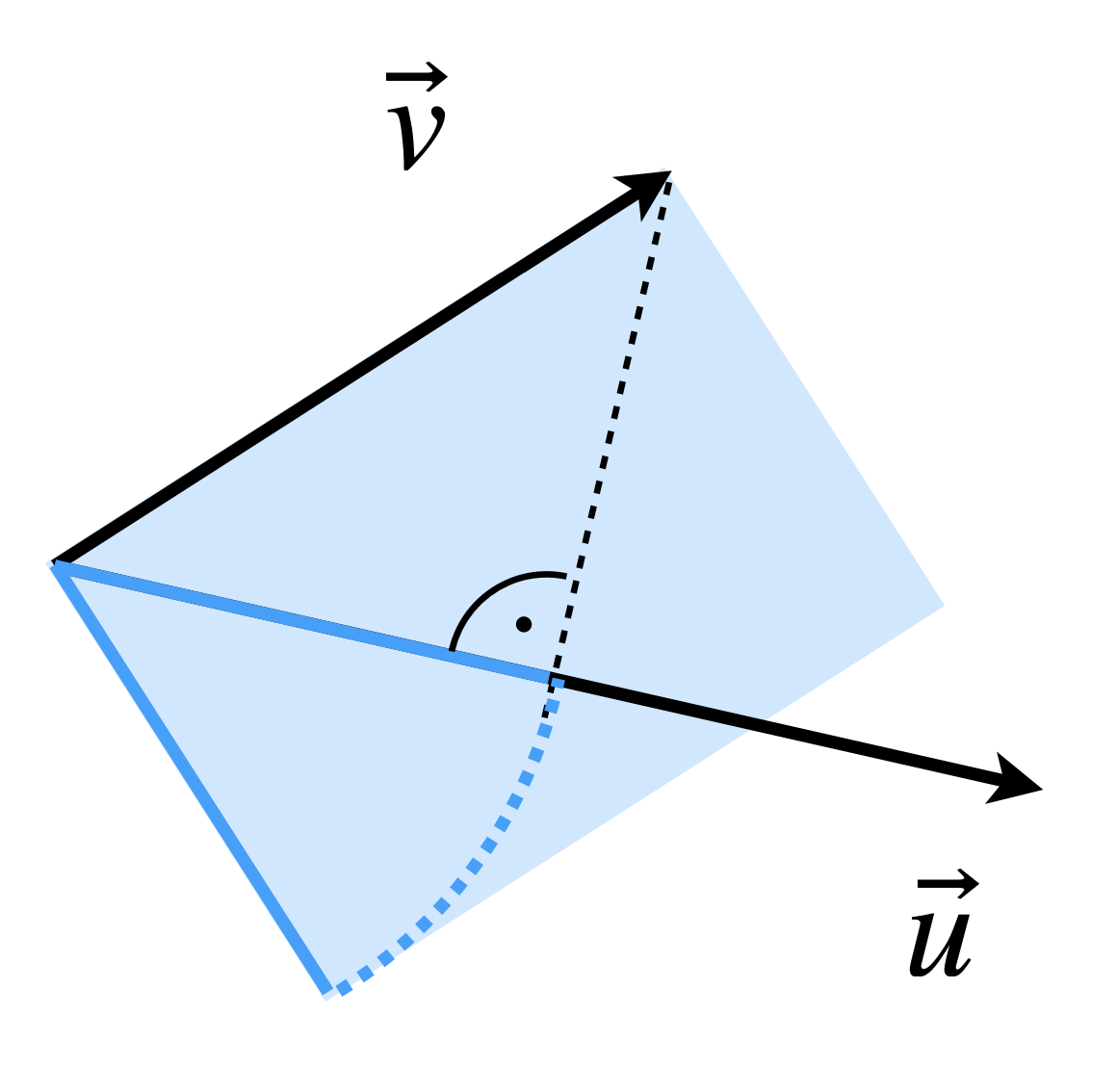
Abb. 11.2: Geometrische Interpretation des Skalarprodukts
Bei einem arithmetischen Zugang sind zwei Vektoren als Tupel gegeben, z. B. \(\vec u = \left(\begin{array}{c} u_1 \\ u_2\\\vdots \\ u_n \end{array}\right)\) und \(\vec v = \left(\begin{array}{c} v_1 \\ v_2\\\vdots \\ v_n \end{array}\right)\), und das Skalarprodukt ist über die Produktsumme \(\left<\vec u, \vec v\right> := \sum\limits_{i=1}^n u_iv_i\) definiert. Dieser Zugang ermöglicht auch die Betrachtung außergeometrischer Probleme, etwa die Aufsummation von Stückpreisen bei entsprechend gegebenen Häufigkeiten.
Der axiomatische Zugang definiert das Skalarprodukt als positiv definitive, symmetrische Bilinearform, d. h. es muss folgende Eigenschaften erfüllen:
\[\begin{align*} \left<\vec u, \vec v \right> &\geq 0\\\left<\vec u,\vec u\right> = 0 &\Leftrightarrow \vec u = 0 \\ \left<\vec u,\vec v\right> &= \left<\vec v,\vec u\right>\\ \left<\vec u+\vec v,\vec w\right> &= \left<\vec u,\vec w\right> + \left<\vec v,\vec w\right>\\ \left<\lambda \vec u,\vec v\right> &= \lambda \left<\vec u,\vec v\right> \end{align*}\]
Der axiomatische Zugang spielt im Schulunterricht i. d. R. keine Rolle. Um einen Zusammenhang zwischen der geometrischen Sichtweise und der Formel über die Produktsumme herzustellen, bietet sich die Betrachtung des Kosinussatzes in einem Dreieck an, dessen Seiten über Vektoren beschrieben werden.
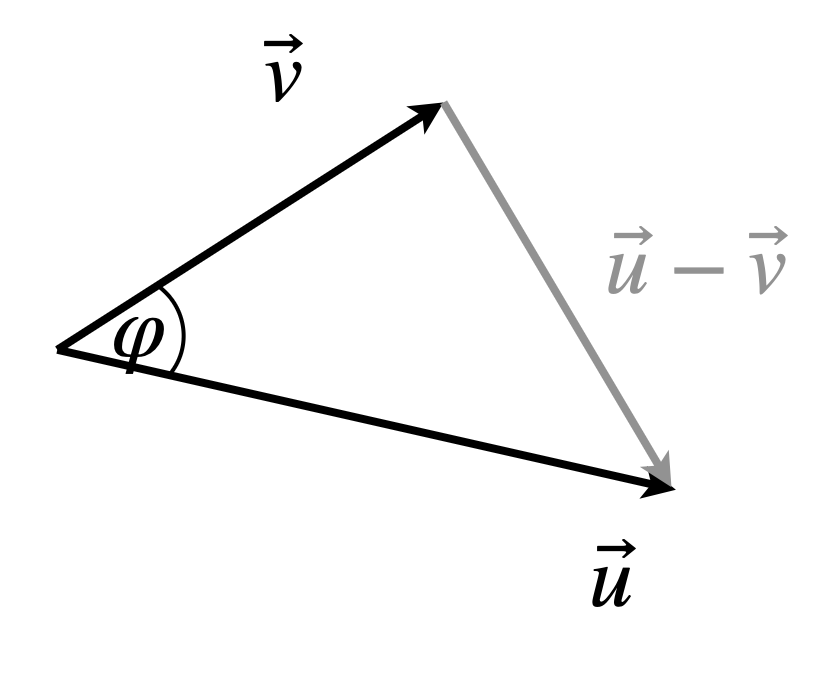
Abb. 11.3: Dreieck zur Herleitung des Skalarprodukts
Die folgenden Betrachtungen werden im \(\mathbb{R}^3\) dargestellt, sind aber auch im \(\mathbb{R}^2\) möglich oder sogar auf den \(\mathbb{R}^n\) übertragbar.
Für die Länge eines Vektors gilt \(|\vec u| = \sqrt{u_1^2+u_2^2+u_3^2}\). Der Kosinussatz für das in Abbildung 11.3 dargestellt Dreieck lautet: \[|\vec u-\vec v|^2 = |\vec u|^2 + |\vec v|^2 - 2\cdot|\vec u|\cdot |\vec v|\cdot \cos(\angle(\vec u,\vec v))\]
Mithilfe der Längenformel und der 2. binomischen Formel links vom Gleichheitszeichen erhält man:
\[\sum_{i=1}^3 (u_i^2-2u_iv_i + v_i^2) = \sum_{i=1}^3 u_i^2 + \sum_{i=1}^2 v_i^2 - 2\cdot|\vec u|\cdot |\vec v|\cdot \cos(\varphi)\]
Dabei heben sich einige Terme auf und es bleibt übrig:
\[\begin{align*}\sum_{i=1}^3 u_iv_i &= |\vec u|\cdot |\vec v|\cdot \cos(\varphi)\\ \cos(\varphi) &= \frac{\sum\limits_{i=1}^3 u_iv_i}{|\vec u|\cdot |\vec v|}\end{align*}\]
Hieraus lässt sich nun motivieren, den im Zähler stehenden Term als Skalarprodukt zu bezeichnen und die Definition \(\left<\vec u, \vec v\right> = \sum\limits_{i=1}^3 u_iv_i\) einzuführen.
Neben der Schreibweise \(\left <\vec u,\vec v\right>\) sind auch \(\vec u\bullet \vec v\) oder \(\vec u\circ \vec v\) üblich. Letztere beiden können jedoch suggerieren, dass aus dem »Produkt« zweier Vektoren wieder ein Vektor entsteht, da dies den Erfahrungen des bisherigen Umgangs mit Produkten entspricht. Die Schreibweise \(\left <\vec u,\vec v\right>\) könnte hier stärker darauf hinweisen, dass es sich um eine »Funktion« handelt, die den beiden Vektoren \(\vec u\) und \(\vec v\) eine Zahl (also ein Skalar) zuordnet.
11.2 Dynamische Geometriesysteme
In dynamischen Geometriesystemen (DGS) wie GeoGebra40 oder Cinderella41 lassen sich geometrische Konstruktionen darstellen und durch zusätzliche Funktionalitäten vielfältig untersuchen.
Zunächst einmal bietet ein DGS die üblichen Grundkonstruktionen, die auch mit Zirkel und Lineal möglich sind, sowie darauf aufbauende Konstruktionen (wie das Einzeichnen einer Mittelsenkrechte zu zwei Punkten). Weiterhin ist es i. d. R. möglich, Objekte auszumessen und die Konstruktion durch weitere graphische Elemente (wie z. B. Texte) zu ergänzen.
Zum Umgang mit DGS gibt es vielfältige Forschungs- und Entwicklungsergebnisse, die auch in den Didaktiken der einzelnen Sachgebiete referenziert werden (u. a. bei Greefrath et al., 2016, 41 f., 65 f., 155 f.; Weigand et al., 2018, 62 ff.).
In der Verwendung von dynamischer Geometriesoftware liegen einige Besonderheiten, auf die hier kurz eingegangen werden soll.
- Die zu betrachtenden Objekte werden i. d. R. zugstabil konstruiert. Das heißt, wenn ein Parallelogramm konstruiert werden soll, muss dies so erfolgen, dass es sich weiterhin um ein Parallelogramm handelt, auch wenn einer seiner Eckpunkte bewegt wird. So wird auch der Unterschied zwischen Konstruieren und Zeichnen deutlich: Die Konstruktion schafft Relationen zwischen den Eckpunkten bzw. Seiten des Parallelogramms, so dass die Parallelogramm-Eigenschaft in das Objekt implementiert wurde, während eine Zeichnung nur statisch ein Parallelogramm darstellt. Der Begriffsbildung (insbesondere dem Begriffsinhalt) dienlich ist auch die Diskussion verschiedener Konstruktionswege bzw. deren Identifizierung anhand des »Bewegungsverhaltens« des konstruiereten Objekts. Einen unterrichtspraktischen Ansatz hierfür liefern Kortenkamp & Dohrmann (2016).

Abb. 11.4: Zugstabil konstruiertes vs. gezeichnetes Parallelogramm
- Dynamische Geometriesysteme verhalten sich entweder deterministisch oder kontinuierlich. Damit ist gemeint, dass die durch eine Konstruktion abhängigen Objekte bei deterministischen Systemen stets dasselbe Verhalten aufweisen und bei dynamischen System, je nach Bewegung der unabhängigen Objekte, unterschiedlich dargestellt werden können. Abbildung ?? visualisiert dieses Verhalten. Der fachliche Hintergrund liegt in der Programmierung eines DGS, was bei Kortenkamp (1999, 84 ff.) und Labs (2008, 57 ff.) ausführlicher dargestellt wird. Für den Schulalltag sollte Ihnen dies bewusst sein, damit Sie »merkwürdiges« DGS-Verhalten verstehen und ggf. erklären können.
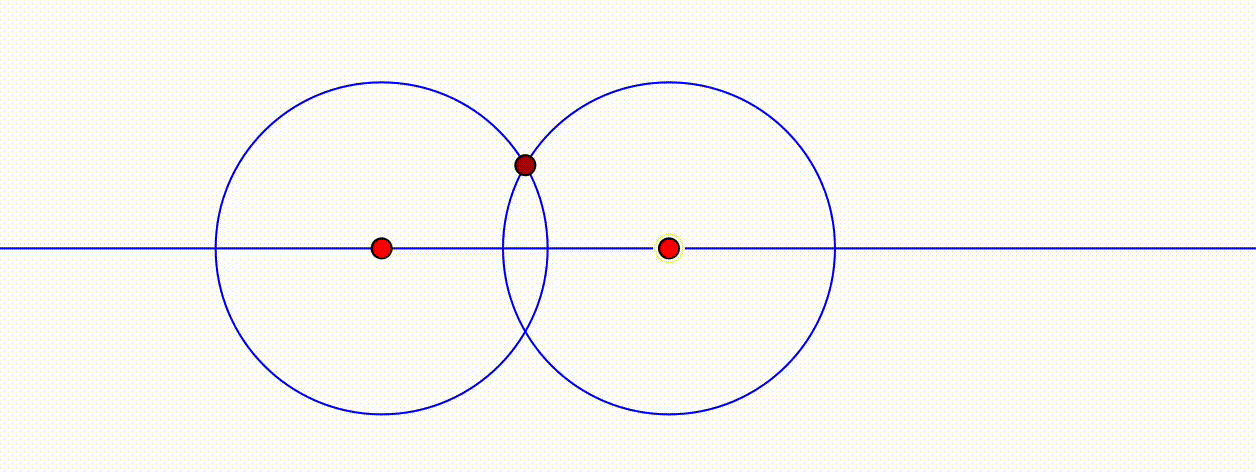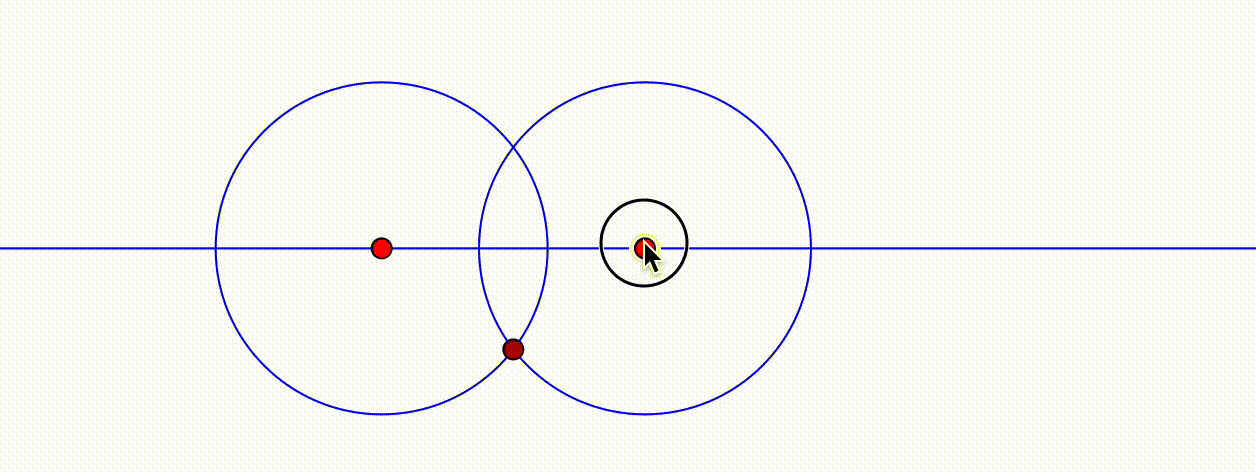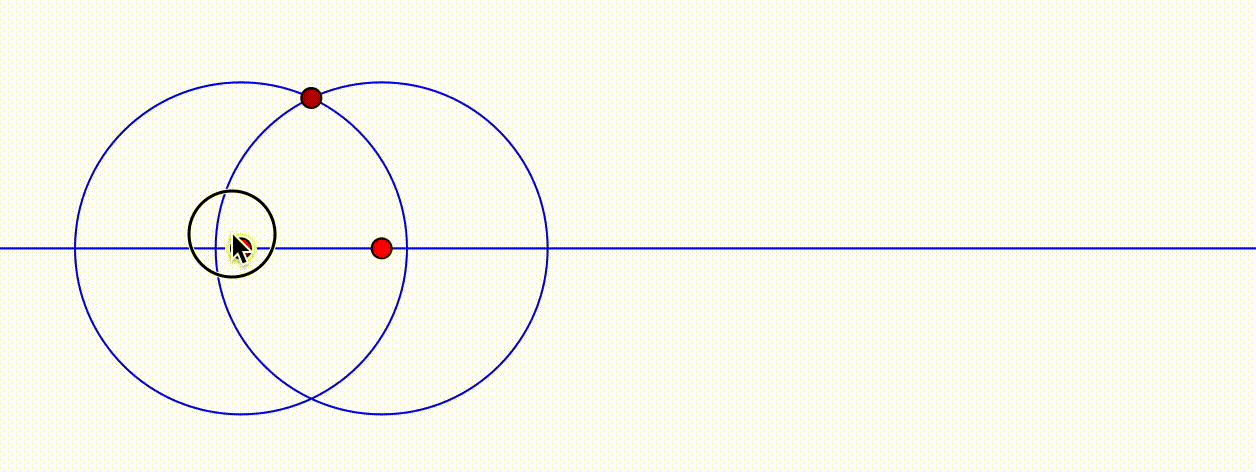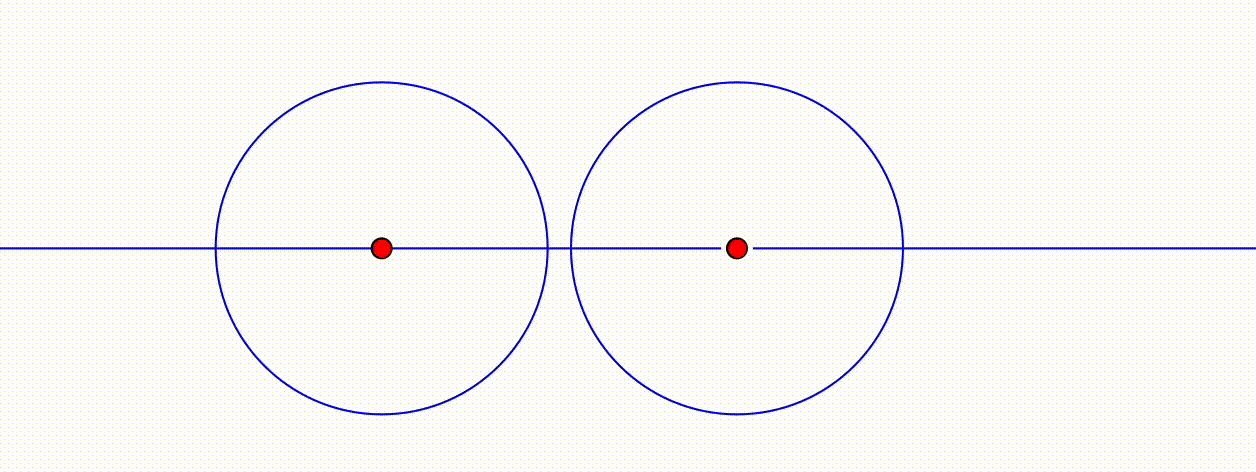
Abb. 11.5: Kontinuierliches Verhalten in Cinderella
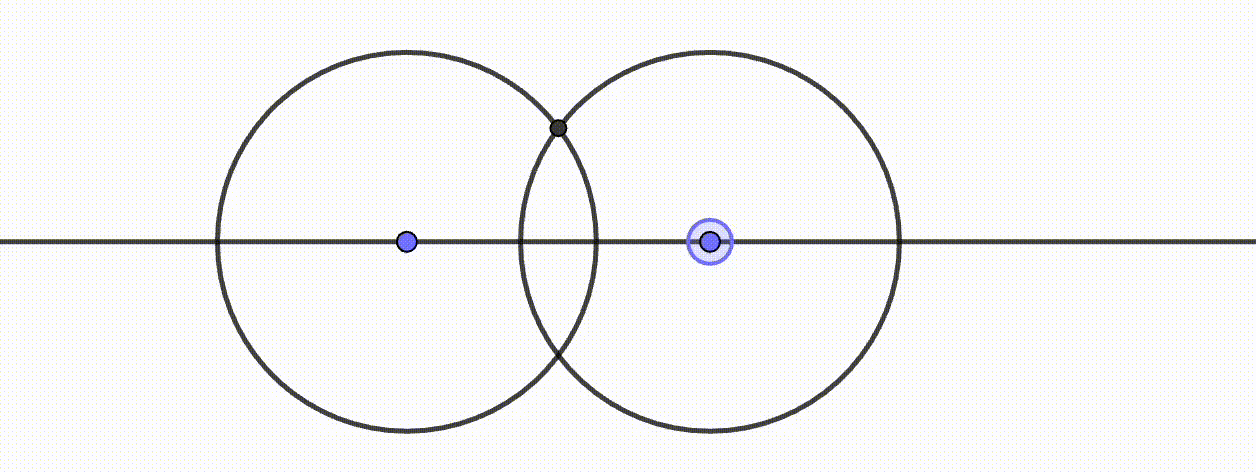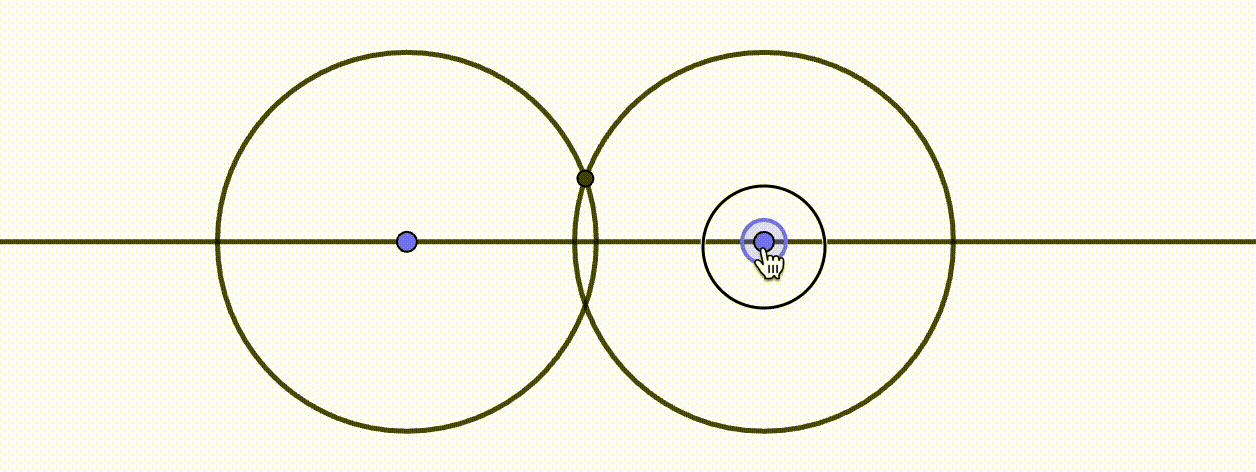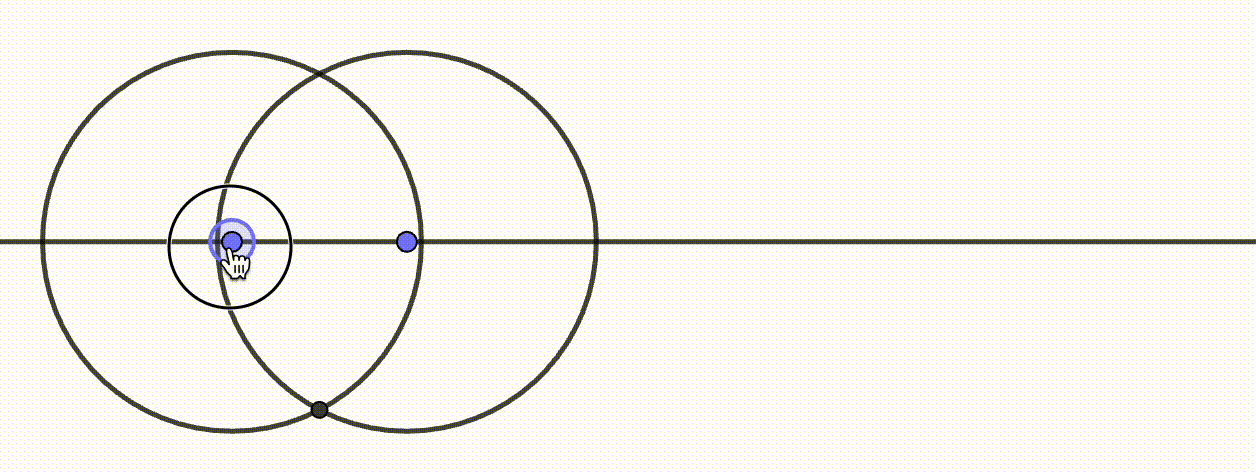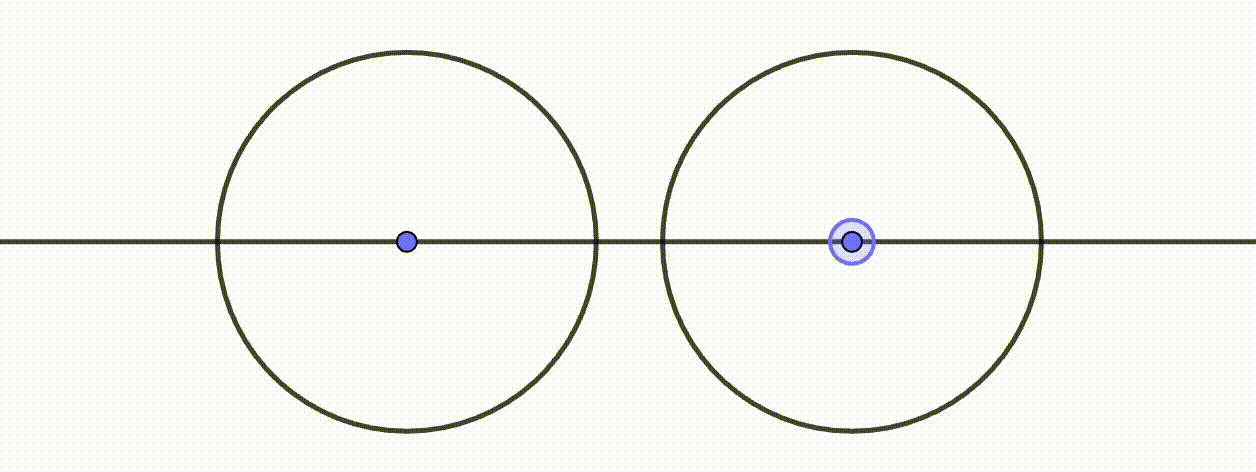
Abb. 11.6: Deterministisches Verhalten in GeoGebra
- Über die Verwendung von Spuren und Ortslinien kann der DGS-Einsatz zu einer intensiveren geometrischen Auseinandersetzung führen als es mit statischen Zeichnungen auf Papier der Fall wäre. Die Spur zeichnen bei Bewegung die Lage eines Objektes nach. Dies ist insbesondere dann von Interesse, wenn ein Objekt von einem anderen abhängig ist und man die Abhängigkeit genauer untersuchen möchte. Die Ortslinie ergibt sich nun als Menge aller Punkte, auf der sich ein Punkt in Abhängigkeit anderer Objekte bewegt. Konstruiert man bzw. über zwei Kreise gleichen Radius einen Punkt \(M\), der von den Punkten \(A\) und \(B\) denselben Abstand hat und varriert die Länge des Radius, so erhält man damit alle Punkte, die von \(A\) und \(B\) gleich weit entfernt sind. Die zugehörige Ortslinie ist dann die Mittelsenkrechte von \(A\) und \(B\).
References
Im Übrigen sind beide Eigenschaften äquivalent zueinander – es lohnt sich, den Beweis dafür einmal durchzuführen.↩︎