2 (Hoch-)Schulmathematik
Ziele
- Sie erkennen den Nutzen der Hochschulmathematik bei der Entscheidungsfindung zur Spezifizierung und Strukturierung der Schulmathematik auf der formalen Ebene des Vier-Ebenen-Ansatzes.
- Sie kennen geeignete Quellen zur Beantwortung der Fragen auf der formalen Ebene des Vier-Ebenen-Ansatz
Material
2.1 Doppelte Diskontinuität
Auf der formalen Ebene des Vier-Ebenene-Ansatzes soll der zu betrachtende Lerngegenstand fachmathematisch untersucht werden, um eine erste Auswahl (Spezifizierung) und Anordnung (Strukturierung) der Lerninhalte zu ermöglichen. Dies ruft natürlich – auch für Lerngegenstände der Grundschulmathematik – danach, die im Studium erworbenen hochschulmathematischen Erkenntnisse zu nutzen. Dieser Ruf wird jedoch (scheinbar!) geschmälert durch eine offensichtliche Ungleichheit zwischen Schulmathematik und Hochschulmathematik. Felix Klein beschreibt dieses Phänomen, das sich insbesondere auf die Ausbildung von Lehrkräften auswirkt, bereits im Übergang vom 19. zum 20. Jahrhunderts als doppelte Diskontinuität: »Der junge Student sieht sich am Beginn seines Studiums vor Probleme gestellt, die ihn in keinem Punkte mehr an die Dinge erinnern, mit denen er sich auf der Schule beschäftigt hat; natürlich vergißt er daher alle diese Sachen rasch und gründlich. Tritt er aber nach Absolvierung des Studiums ins Lehramt über, so soll er plötzlich eben diese herkömmliche Elementarmathematik schulmäßig unterrichten; da er diese Aufgabe kaum selbständig mit seiner Hochschulmathematik in Zusammenhang bringen kann, so wird er in den meisten Fällen recht bald die althergebrachte Unterrichtstradition aufnehmen, und das Hochschulstudium bleibt ihm nur eine mehr oder minder angenehme Erinnerung, die auf seinen Unterricht keinen Einfluß hat.« (Klein, 1967, S. 1)3
Einen Ausweg, dieser doppelten Diskontinität zu entgehen, sah Klein in einer Elementarmathematik vom höheren Standpunkte aus (Klein, 1925, 1955, 1967). Dabei verfolgt er »das Ziel, im Anschluss an umfassende hochschulmathematische Erfahrungen die Schulmathematik in den erworbenen Wissenskanon fachlich einzubetten« (Danckwerts, 2013, S. 78).
Diesen Gedanken fortsetzend kann man auch »gleich am Anfang des Studiums direkt und explizit an die schulmathematischen Vorerfahrungen an[knüpfen], bleibt inhaltlich bei diesen und arbeitet einen höheren Standpunkt heraus, der auf die vertiefte Auseinandersetzung mit der Oberstufenmathematik zielt und prinzipiell mit den bis dahin erworbenen (elementar-)mathematischen Mitteln auskommt.« (Danckwerts, 2013, S. 78) Eine solche Entwicklung hat das Projekt Mathematik Neu Denken verfolgt, das gut 100 Jahre nach Kleins Publikationen die Lehramtsausbildung im Fach Mathematik weiterentwickeln wollte (Beutelspacher et al., 2012). Entwickelt wird daraus eine Schulmathematik vom höheren Standpunkt, die auf eine fachliche und verstehensorientierte Durchdringung der Schulmathematik zielt, »ohne im vollen Umfang auf das Instrumentarium der kanonischen […] [Hochschulmathematik] zurückgreifen zu müssen« (Danckwerts, 2013, S. 87).
Im Rahmen der Stoffdidaktik-Veranstaltung sollen beide Ansätze aufgegriffen und an konkreten Beispielen versucht werden, die Fragen der formalen Ebene zu beantworten. Als bedeutsames Bindeglied zwischen Schul- und Hochschulmathematik stellen sich dabeifundamentale Ideen heraus, die auch schon auf die semantische Ebene des Vier-Ebenen-Ansatzes zielen – siehe dazu Abschnitt 3.4.
2.2 Geeignete Quellen
Neben den Werken von Felix Klein zu Beginn des 20. Jahrhunderts (Klein, 1925, 1955, 1967) und aktuellen Ansätzen zum Umgang mit der doppelten Diskontinuität in der Lehramtsausbildung (Ableitinger et al., 2013; Beutelspacher et al., 2012) liefern die in den 1970er Jahren von Hans Freudenthal verfassten Werke zur Mathematik als pädagogische Aufgabe (Freudenthal, 1973c, 1973b; englischsprachig auch digital verfügbar über Freudenthal, 1973a) Ansätze, Schul- und Hochschulmathematik miteinander in Bezug zu bringen.
Ebenfalls hilfreich sind größere Nachschlagewerke zur Mathematik, bspw. die Kleine Enzyklopädie Mathematik (Gellert et al., 1986).
Nicht zu unterschätzen für die fachmathematische Auseinandersetzung sind auch fachdidaktische Quellen, insbesondere zur Didaktik der Sachgebiete. Als digital verfügbare Quellen seien zu erwähnen:
- Didaktik der Algebra: nach der Vorlage von Hans-Joachim Vollrath (Weigand et al., 2022)
- Didaktik der Geometrie für die Sekundarstufe I (Weigand et al., 2018)
- Didaktik der Analysis. Aspekte und Grundvorstellungen zentraler Begriffe (Greefrath et al., 2016)
- Didaktik der Stochastik in der Sekundarstufe I (Krüger et al., 2015)
- Didaktik der Analytischen Geometrie und Linearen Algebra: Algebraisch verstehen – Geometrisch veranschaulichen und anwenden (Henn & Filler, 2015)
- Mathematikunterricht in der Sekundarstufe II. Band 1: Fachdidaktische Grundfragen, Didaktik der Analysis (Tietze et al., 2000a)
- Mathematikunterricht in der Sekundarstufe II. Band 2: Didaktik der Analytischen Geometrie und Linearen Algebra (Tietze et al., 2000b)
- Mathematikunterricht in der Sekundarstufe II. Band 3: Didaktik der Stochastik (Tietze et al., 2002)
Ebenfalls hilfreich für die fachliche Spezifizierung und Strukturierung kann die Darstellung der Fachinhalte in Schulbüchern sein. Hier bietet sich eine vergleichende Analyse mehrerer Schulbücher, auch unterschiedlicher Bundesländer, an.
Nur gering geeignet für die Spezifizierung und Strukturierung sind die Bildungsstandstandards und Rahmenlehrpläne. Sie bieten – entsprechend ihrer Funktion – bereits eine Auswahl der zu unterrichtenden Inhalte und schränken damit die fachdidaktische Diskussion diesbezüglich ein.
2.3 Beispiel Negative Zahlen
Am Beispiel der negativen Zahlen soll dargestellt werden, wie eine Sichtweise vom höheren Standpunkt auf die in der Schule relevante Behandlung dieses Lerngegenstands zur Spezifizierung und Strukturierung helfen kann. Dabei beinhalten die negativen Zahlen sowohl die ganzen Zahlen als auch die rationalen Zahlen.
2.3.1 Natürliche Zahlen
Fachmathematisch können die ganzen Zahlen aus den natürlichen Zahlen generiert werden. Hierzu sollen zunächst die natürlichen Zahlen selbst fachmathematisch eingeordnet werden. Im Prinzip bestehen zwei Sichtweisen, nämlich die Einführung über die Peano-Axiome sowie die Betrachtung gleichmächtiger Mengen.
Aus den Peano-Axiomen (Wikipedia, 2021) folgt zunächst die Existenz einer Reihenfolge von Zahlen (also Nachfolger der \(0\)), die dann mit \(1\), \(2\), \(3\) usw. bezeichnet werden können.4 Diese Bezeichnung erlaubt jedoch noch keinerlei Berechnungen, nicht einmal eine Ordnungsrelation ist vorhanden. Es kann also (noch) nicht gesagt werden, dass \(3\) größer ist als \(1\). Vielmehr lässt sich die Situation eher mit einem Alphabet vergleichen5, bei dem auch nicht C größer als A ist.
Für eine Ordnungsrelation bedarf es zunächst der Definition der Addition über \(n+0 := n\) und \(n+k' := (n+k)'\) für alle \(n,k\in\mathbb{N}\) mit der (aus den Peano-Axiomen existierenden) Nachfolgerbildung \('\). So gilt etwa mit \(1:=0'\): \({\color{blue} 1}+{\color{red} 1} = {\color{blue} 1}+{\color{red} {0'}} = ({\color{blue} 1}+{\color{red} 0}){\color{red} '} = 1{\color{red} '} =: 2\). So kann nun induktiv jede höhere Additionsaufgabe generiert werden. Darauf aufbauend kann die Ordnungsrelation \(n<m\) über die Existenz eines \(k\in\mathbb{N}\backslash\{0\}\) mit \(m = n+k\) definiert werden. Die Subtraktion \(m-n = k\) ist nun wiederum über die Umkehroperation \(n+k = m\) definierbar, sofern \(m\geq n\).
Die Gleichmächtigkeit (z. B. endlicher) Mengen \(M\) und \(N\) wird über die Existenz einer Bijektion zwischen diesen beiden Mengen definiert, siehe Abbildung 2.1.
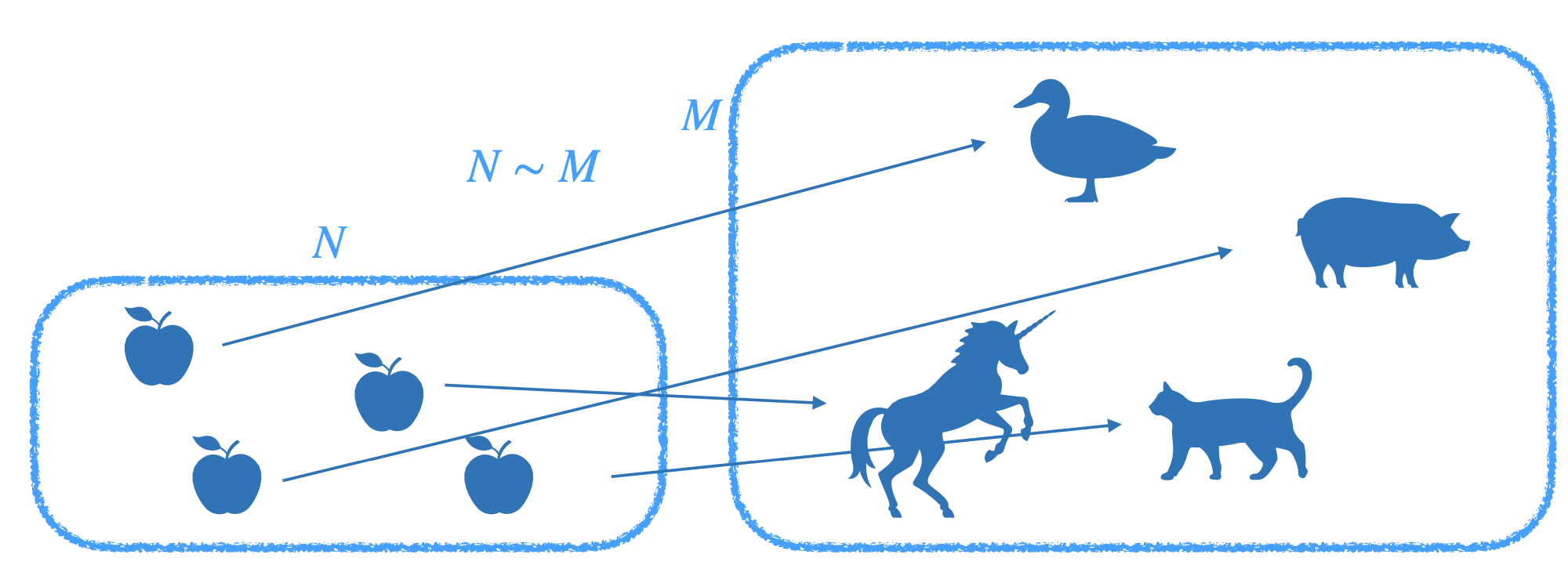
Abb. 2.1: Gleichmächtigkeit von Mengen
Diese Relation ist eine Äquivalenzrelation, also symmetrisch, reflexiv und transitiv. Damit können Äquivalenzklassen gebildet werden, die die Mächtigkeit der Menge angeben. \(4\) ist dann der Bezeichner für die Äquivalenzklasse von vierelementigen Mengen. Die Addition \(n+k\) entspricht dann der Mächtigkeit der Vereinigungsmenge von Mengen mit den Mächtigkeiten \(n\) und \(k\), vgl. Abbildung 2.2.

Abb. 2.2: Additionsergebnis als Äquivalenzklasse der Vereinigungsmenge
2.3.2 Ganze Zahlen
Da innerhalb der natürlichen Zahlen noch nicht beliebig subtrahiert werden darf, stehen auch keine negativen Zahlen als Ergebnisse zur Verfügung. Um dennoch das Ergebnis bspw. der Aufgabe \(2-7\) »definieren« zu können, bietet sich erneut eine Äquivalenzrelation über die »Differenzengleichheit« an. Konkret lässt sich für \(k,l,m,n\in\mathbb{N}\) sagen: \((k,l)\sim (m,n):\Leftrightarrow k+n=l+m\) Das heißt z. B., dass die Zahlenpaare \((2,7)\), \((0,5)\) und \((4,9)\) in Relation zueinander stehen, weil sie dieselbe »Differenz« haben (obwohl es die Differenz formal noch nicht gibt). Dies ermöglicht nun die Einführung des Bezeichners \(-5\) für die Äquivalenzklasse \([(0,5)]\).
Das Vorgehen ist verträglich mit den bisherigen Regeln in \(\mathbb{N}\), d. h. es führt nicht zu Widersprüchen, wenn etwa das Zahlenpaar \((7,4)\) betrachtet wird mit dem Repräsentanten-Bezeichner \(3\). Die Menge aller Äquivalenzklassen (bzw. deren Kurzbezeichner) ist nun \(\mathbb{Z}\).
Die Addition und Subtraktion zweier Zahlenpaare sind nun definierbar:
\[\begin{align} (k, l) + (m, n) := (k + m, l + n)\\ (k, l) − (m, n) := (k, l) + (n, m) \end{align}\]
Als Alternative bietet sich ein axiomatisches Vorgehen an, also dass die ganzen Zahlen mit der Addition als abelsche Gruppe definiert werden – bedeutsam ist hier insbesondere die Existenz eines Inversen zu jeder Zahl.
2.3.2.1 Permanenzprinzip und Permanenzreihen
Wie bereits erwähnt, führen die neu eingeführte Addition und Subtraktion in \(\mathbb{Z}\) nicht zu Konflikten mit den bisherigen analogen Operationen in \(\mathbb{N}\). Dies wird über das Permanenzprinzip gefordert, nach dem neue Theorien (z. B. das Rechnen mit negativen Zahlen) soweit wie möglich verträglich sein müssen mit bisherigen Theorien (z. B. das Rechnen mit positiven Zahlen).
Sichtbar gemacht werden kann dieses Prinzip über Permanenzreihen. Dies ist insbesondere dann hilfreich, wenn für bestimmte Rechenoperationen keine geeigneten realen Veranschaulichungen existieren. Ein typisches Beispiel hierfür ist die Multiplikation zweier negativer Zahlen. Kann die Multiplikation einer natürlichen Zahl (erster Summand) mit einer negativen Zahl (zweiter Summand) außermathematisch noch als mehrfache Verschuldung aufgefasst und die Vertauschung von erstem und zweitem Summanden über das Kommutativgesetz innermathematisch erklärt werden, bietet die Multiplikation zweier negativer Zahlen keine so naheliegende Interpretation. Abbildung 2.3 stellt eine Permanenzreihe dar, anhand derer die Rechnung \((-3)\cdot (-5)\) erklärt werden kann.
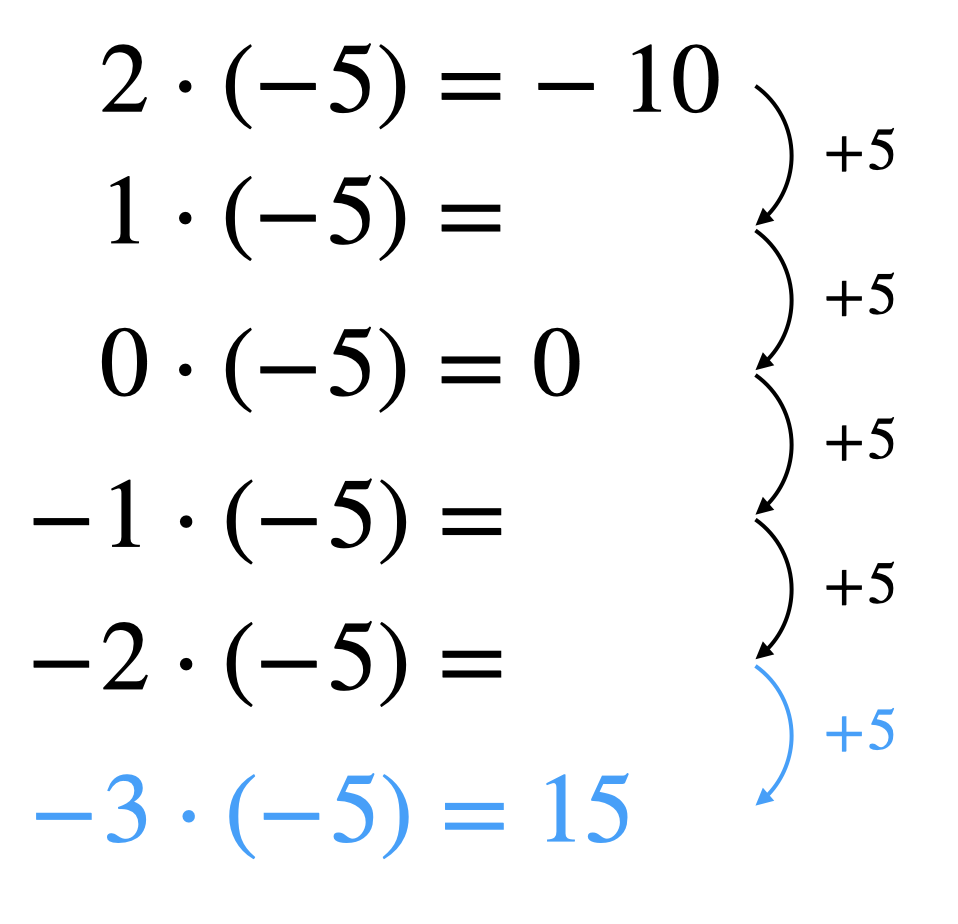
Abb. 2.3: Permanenzreihe zur Multiplikation zweier negativer Zahlen
Entscheidend ist beim Aufstellen von Permanenzreihen jedoch, dass der Übergang von einer Zeile zur nächsten auf einem entsprechenden Rechengesetz beruht. Im Abbildung 2.3 ist dies das Distributivgesetzt \((a-1) \cdot b = a \cdot b - b\). Varnachlässigt man die Existenz einer Übergangsregel, lassen sich plausibel erscheinende Muster fortsetzen (wie \(0^3 = 0\), \(0^2 = 0\), \(0^1 = 0\)), die dann allerdings zu falschen Schlussfolgerungen (\(0^0 = 0\)) führen. Im dargestellten Beispiel kann die Übergangsregel \(a^{m-1} = a^m : a\) wegen \(a = 0\) nicht angewandt werden.
2.3.2.2 Ableitungen für den Lernpfad
Aus all den bisherigen Überlegungen auf der formalen Ebene lassen sich für den Unterricht zentrale Fachinhalte ableiten:
Ganze Zahlen können über Zahlenpaare aus den natürlichen Zahlen oder als »Gegenzahlen« der natürlichen Zahlen entwickelt werden.
- Natürliche Zahlen sind als Teilmenge in die ganzen Zahlen eingebettet.
- Die Subtraktion natürlicher Zahlen \(m-n\) mit \(n > m\) ist nun lösbar.
- Die Rechenregeln werden erweitert, wobei die bekannten weiter gelten. Die wird über das Permanenzprinzip begleitet, bei der Herleitung von Rechenregeln bietet sich die Nutzung von Permanenzreihen an.
2.3.3 Rationale Zahlen
In fachlich analoger Weise lassen sich auch die rationalen Zahlen über Äquivalenzrelationen einführen. Dann fordert die »Quotientengleichheit«, dass für \(k,l,m,n\in\mathbb{N}\) mit \(l,n\neq 0\) gilt: \((k,l)\sim (m,n):\Leftrightarrow k\cdot n=l\cdot m\). Die Äquivalenzklasse \([(1,2)]\) kann dann mit \(\frac{1}{2}\) bezeichnet werden. Im Gegensatz zu den ganzen Zahlen ist es bei den rationalen Zahlen durchaus üblich, für dieselbe Zahl unterschiedliche Bezeichner zu verwenden, wie \(\frac{1}{2}\) oder \(\frac{5}{10}\). Fachmathematisch ist dies jedoch nicht relevant, also auch keine Diskussion auf der formalen Ebene (jedoch auf späteren Ebenen).
Aus Sicht der formalen Ebene lässt sich daher auch nicht ableiten, ob im Mathematikunterricht nach den natürlichen Zahlen zunächst die rationalen Zahlen (wie z. B. in Deutschland) oder erst die ganzen Zahlen (wie z. B. in Australien) eingeführt werden sollten. Innerhalb eines Zahlbereichs bietet jedoch die fachlogische Struktur Ansatzpunkte zur Gestaltung des Lernpfads, wie bei den negativen Zahlen dargestellt.
2.4 Zum Nachbereiten
- Nutzen Sie verschiedene fachmathematische und fachdidaktische Quellen sowie Schulbücher, um fachlich zu klären, was »Terme« und »Gleichungen« sind.
- Nutzen Sie Permanenzreihen, um weitere Rechengesetze nachzuvollziehen, z. B. dass \(a^0 = 1\) (\(a\neq 0\)) und \(a^\frac{1}{2} = \sqrt{a}\) (\(a \geq 0\)) ist.
References
Es handelt sich hier um den Nachdruck eines Werke, dessen erste Auflage 1908 erschien.↩︎
Ab 10 wird bei der Bezeichnung jedoch das Stellenwertsystem genutzt – das geht schon weiter als hier zulässig.↩︎
Ein wesentlicher Unterschied dieses Vergleiches ist, dass das Alphabet endlich ist, die Menge der natürlichen Zahlen jedoch nicht.↩︎