10 Intermezzo: Arithmetisches Mittel
Ziele
- Sie können die Strukturierung einer Unterrichtsstunde zum arithmetischen Mittel nachvollziehen.
- Sie erkennen den Nutzen stoffdidaktischer Analysen und tätigkeitstheoretischer Modelle für die strukturierte Planung von Mathematikunterricht.
- Sie kennen die Lehrstrategie des Aufsteigens vom Abstrakten zum Konkreten als weitere Möglichkeit, Begriffe zu bilden.
Material
- Folien zum Kapitel 10 (pdf, Keynote)
- Virtuelles Arbeitsmittel zum Medien und arithmetischen Mittel (html, Cinderella)
In diesem Kapitel sollen die in den letzten beiden Kapitel dargestellten Theorien auf die Planung einer 45-minütigen Unterrichtsstunde zum arithmetischen Mittel angewandt werden. Es handelt sich dabei nicht um eine ausführliche Unterrichtsplanung – für diese wäre mindestens noch eine Bedingungsanalyse der zu unterrichtenden Klasse und eine ausführlichere didaktisch-methodische Diskussion notwendig. Vielmehr soll im Groben dargestellt werden, welche theoriebasierten Gedankengänge in die Strukturierung einer Unterrichtsstunde fließen können.
10.1 Stoffdidaktische Hintergründe
Das arithmetische Mittel ist ein Lagemaß und ist daher in den Lernbereich der Lage- und Streumaße einzuordnen. Bedeutsame Begriffe sind demnach das arithmetische Mittel, der Median und der Modalwert, die Spannweite, Varianz und Standardabweichung, sowie ggf. noch das untere und obere Quartil bzw. Ausreißer. Sachverhalte und Verfahren spielen in dem Lernbereich keine so große Rolle. Gegebenenfalls ist mit Blick auf die Oberstufe und die Anwendung im Zusammenhang mit Erwartungswerten noch der Steinersche Verschiebungssatz28 von Relevanz.
Als Lagemaß bedarf das arithmetische Mittel metrisch skalierter Daten, also Daten, mit denen aufgrund ihrer inneren Anordnung und Skalierung gerechnet werden darf.29 Dem gegenüber stehen ordinal skalierte Daten, die sich nur in eine Reihenfolge bringen lassen oder nominal skalierte Daten, die mithilfe von Bezeichnungen beschrieben werden. Dabei kann jede metrische Skala auch als ordinale und jede ordinale Skala auch als nominale Skala aufgefasst werden. Diese Unterscheidung ist insbesondere dann relevant, wenn die verschiedenen Lagemaße miteinander verglichen werden, da für ordinal skalierte Daten auch der Median und für nominal skalierte Daten der Modalwert bestimmt werden können.

Abb. 10.1: Beispiele für metrische, ordinale und nominale Skalen
Hat man eine Messreihe mit den \(n\) Daten \(x_1,x_2,\ldots,x_n\) gegeben, lässt sich das arithmetische Mittel \(\bar{x}\) berechnen über
\[\bar{x} = \frac{x_1+x_2+\ldots + x_n}{n} = \frac{\sum\limits_{i=1}^n x_i}{n} = \sum_{i=1}^n \frac{x_i}{n}\]
In der Schule üblich ist die erste Schreibweise, in der keine Summenzeichen verwendet werden. Es gibt auch die Möglichkeit, die Berechnung nur über ihre Vorschrift einzuführen: »Bilde die Summe aller Werte und dividiere durch die Anzahl aller Werte.« (vgl. Krüger et al., 2015, S. 56).
Diese Sichtweise wird in der Oberstufe für nicht-diskrete Daten mithilfe des Integrals erweitert über \(\bar{x} = \frac{\int\limits_a^b f(x)}{b-a}\).
Nach Krüger et al. (2015, 56 f.) enthält das arithmetische Mittel folgende Aspekte:
- Es handelt sich um eine fiktive Größe, die von keinem der Messwerte erreicht werden muss bzw. im Kontext auch gar nicht realistisch erscheinen muss (wenn es sich zum beispiel um Messungen mit natürlischen Zahlen handelt, kann das arithmetische Mittel dennoch eine Bruchzahl sein).
- Das arithmetische Mittel kann als Vergleichswert eines jeden Messwertes aufgefasst werden.
- Damit ist das arithmetische Mittel auch ein Prognosewert, der eine Einschätzung darüber gibt, in welcher Größenordnung ein Messwert (vermutlich) liegen wird.
- Außerdem kann das arithmetische Mittel als repräsentativer Wert einer kompletten Messreihe aufgefasst werden – also die eigentliche Eigenschaft des Lagemaßes annehmen.
Als Grundvorstellungen werden von Krüger et al. (2015, 57 ff.) genannt, dass das arithmetische Mittel als Ausgleichwert sowie als Wert einer gleichmäßigen Verteilung aufgefasst werden kann. Letzere Vorstellung ermöglicht die Repräsentation, die \(n\) Werte als Strecken nebeneinander und im Vergleich dazu \(n\) gleich lange Strecken mit gleicher Gesamtlänge darzustellen (siehe Abbldung 10.2).
Hinsichtlich der Kernfragen bietet es sich an, den Nuten von Lage- und Streumaßen zu hinterfragen:
- Allgemein dienen Lage- und Streumaße – neben Diagrammen – dem Vergleich statistischer Erhebungen, also könnte eine Kernfrage lauten: Wie kann ich statistische Erhebungen rechnerisch miteinander vergleichen?
- Konkret auf Lagemaße bezogen, ließe sich die präzisieren: Wie kann ich die vielen Ergebnisse einer Messreihe mit nur einem Wert beschreiben?
- Die Besonderheit des arithmetischen Mittel, dass dieses bei metrisch skalierten Daten tatsöchlich eine berechnet Zahl ergibt, könnte folgendertmaßen betont werden: Wie kann ich das durchschnittel Ergbnis einer Messreihe berechnen?
Als sinnstifender Kontext bieten sich Sportliche Leistungen an, da diese den Schülerinnen und Schülern vertraut sind (Lebensweltbezug), Lage- und Streumaße tatsächlich zu ihrem Vergleich herangezogen werden (Authentizität) und über vielfältige Sportarten die weiteren Lage- und Streumaße am Kontext besprochen werden können (Reichhaltigkeit). Außerdem bietet sich dieser Kontext für fächerübergreifende oder projektartige Herangehensweisen an.
10.2 Kompetenzziele
Im Gegensatz zu den Lernzielen, die ein psychisches Konstrukt der Lernenden sind (vgl. Abschnitt 8.2.2), beschreiben die Kompetenzziele, über welche Kompetenzen die Schülerinnen und Schüler am Ende der Unterrichtsstunde neu verfügen sollen. Beim konkreten Lerngegenstand sind für eine 45-minütige Unterrichtsstudne realistisch:
- Die Schülerinnen und Schüler können das arithmetische Mittel einer Messreihe berechnen.
- Die Schülerinnen und Schüler können erklären, wofür man des arithmetischen Mittel benötigt.
10.3 Unterrichtsphasen
Im folgenden wird davon ausgegangen, dass für diese Unterrichtsstunde keine explizite Sicherung des Ausgangsniveaus notwendig ist. Diese Entscheidung kann niemals pauschal, sondern muss immer abhängig von der konkreten Klasse und der Lehr-Lern-Situation getroffen werden. Hier wird von einer Klasse ausgegangen, die das Addieren und Dividieren (was für die Berechnung des arithmetischen Mittels notwendig ist) beherrscht und aufgrund des aktuellen Mathematikunterrichts Erfahrungen im Umgang mit Daten hat.
10.3.1 Motivierung und Zielbildung
Als auszuprägended Lernziel bietet sich einer Orientierung an der Kernfrage an (vgl. Abschnitt 8.4), so dass am Ende dieser Unterrichtsphase formuliert werden sollte: Wir wollen lernen, wie man das durchschnittliche Ergebnis einer Messreihe berechnen kann.
Im Kontext des Vergleichs sportlicher Leistung kann nun eine Anforderungssituation in der Zone der nächsten Entwicklung gesucht werden. Hierbei sollte nicht offensichtlich sichtbar sein, welche Person die besseren durchschnittlichen Leistungen erbracht hat, um eine Motivation für die Beschäftigung mit dem Lerngegenstand zu schaffen. Das heißt, wenn bspw. die sportlichen Leistungen zweier Personen miteinander verglichen werden:
- Die beiden Personen dürfen nicht gleich viele Versuche durchgeführt haben, da sonst einfach die Summe der Ergebnisse miteinander verglichen werden kann.
- Die Messreihe mit weniger Daten darf keine größere Summe aufweisen als die Messreihe mit mehr Daten, da sonst eine Berechnung zum Vergleich nicht notwendig ist.
Eine mögliche Aufgabenstellung könnte lauten:
Luca und Alex haben Weitsprung geübt. Wer von den beiden ist besser?
Lucas Sprungweiten: 3,20 m; 1,90 m; 3,00 m; 2,90 m
Alex’ Sprungweiten: 3,10 m; 2,90 m; 2,70 m; 2,60 m; 3,00 m
Alternativ wäre es auch möglich, mit den Schülerinnen und Schülern Messwerte aufzunehmen. Diese müssen dann jedoch die oben genannten Kriterien erfüllen. Eine Entscheidung, welcher Weg getroffen wird, ist auch von den konkreten Rahmenbedingungen abhängig.
Eine mögliche Abfolge zur Gestaltung dieser Phase könnte sein:
- Die in der Aufgabenstellung präsentierte Situation wird im Plenung oder im Rahmen einer Murmelphase analysiert und es werden Vorschläge zur Lösung eingeholt. Möglich Impulse könnten sein: Wie kann ich die beiden miteinander vergleichen? Was heißt es, besser zu sein?
- Anschließend kann das Lernziel gemeinsam im Gespräch herausgearbeitet werden. Ergänzend zur obigen Formulierung bietet es sich an, zu betonen: Wir wollen nicht nur herausfinden, wer besser ist, sondern wollen lernen, wie wir das herausfinden.
10.3.2 Stoffvermittlung
Da die Vorgehensweise zur Berechnung des arithmetischen Mittels nicht allzu kompliziert ist, bietet es sich an, dass diese von den Schülerinnen und Schülern selbstständig über einen geführten Arbeitsauftrag erarbeitet wird. Um damit die spätere Definition und eine geeignete Repräsentation vorzubereiten, kann diese im Arbeitsauftrag bereits enthalten sein.
- Begründe, warum es nicht ausreicht, die Gesamtweiten von Luca und Alex miteinander zu vergleichen.
- Zeichne dir die Sprungweiten für Luca in einem geeigneten Maßstab nebeneinander. Stell dir vor, Luca wäre jedes mal gleich weit gesprungen. Wie weit wäre das bei der gleichen Gesamtweise jeweils gewesen?

- Wiederhole das Vorgehen mit Alex’ Sprungweiten vergleiche anschließend die durchschnittlichen Leistungen der beiden.
Die Bearbeitung dieser Aufgabenfolge bietet sich in Parnerarbeit an. Anschließend kann im Plenum die systematische Stofferarbeitung erfolgen:
- Es wird zunächst kurz die Begründung zum ersten Arbeitsauftrag besprochen.
- Anschließend beschreiben einzelne Schülerinnen und Schüler ihr Vorgehen beim zweiten Arbeitsauftrag. Dies unterstützt auch den Übergang von der materialisierten zur sprachlichen Handlung zur Aneignung des Lerngegenstands (vgl. Abschnitt 8.3.2).
- Die Resultate zum dritten Arbeitsauftrag sollten selbstverständlich auch besprochen werden. An dieser Stelle muss jedoch darauf aufmerksam gemacht werden, dass das konkrete Ergebnis gar nicht so relevant ist wie der Weg, auf dem zu den Ergebnis gekommen wurde. Hier bietet sich daher ein Bezug zum ursprünglich ausgearbeiteten Lernziel an.
- Nun kann unabhängig vom Sport-Kontext das allgemeine Vorgehen herausgearbeitet werden, also dass zunächst alle Werte addiert und anschließend durch die Anzahl der Werte dividiert wird. Auch hier können entsprechende Impule genutzt werden: Was muss man also allgemein tun, wenn man eine Messreihe hat und den durchschnittlichen Wert bestimmen möchte?
- Erst nach dieser inhaltlichen Erarbeitung sollte der Bezeichner »arithmetisches Mittel« eingeführt werden, da der neue Begriff nun mit einem inhaltlichen Verständnis verknüpft werden kann.
- Anschließend kann eine Defition und Vorgehensweise zur Berechnung des arithmetischen Mittels notiert werden. Hier bietet es sich an, wieder auf die bereits verwendete Repräsentation einzugehen. Abbildung 10.2 zeigt einen möglichen Hefteraufschrieb.
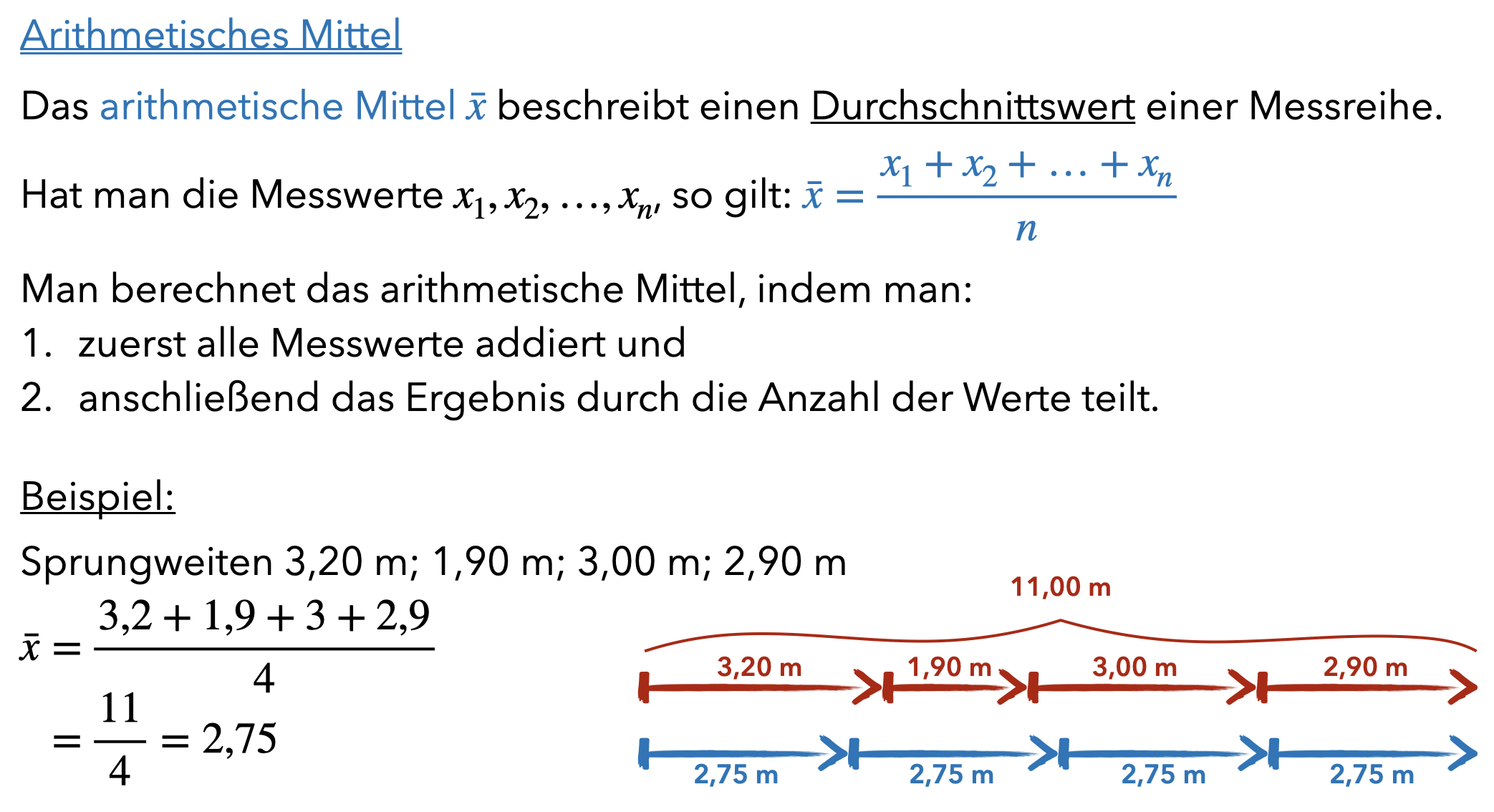
Abb. 10.2: Hefteraufschrieb zum arithmetischen Mittel
Dazu einige Kommentare:
- Es erfolgt zunächst eine Beschreibung, wofür man das arithmetische Mittel verwendet und anschließend erst die formale Definition.
- Die in der Definition enthaltene Vorgehensbeschreibung kann als Orientierungshilfe angesehen werden, um den Begriff des arithmetischen Mittels zu realisieren (vgl. Abschnitte @ref(orientierungsgrundöagen) und 9.1.2).
- Das Beispiel und die Repräsentation sind Bestandteil des Aufschriebs der Definition in den Hefter, um den Schülerinnen und Schüler Anknüpfungspunkte zu bieten.
Um eine Erstaneignung zu ermöglichen, sollten nun einfache Identifizierungs- und Realisierungsaufgaben bearbeitet werden. Dies kann bspw. in Partnerarbeit geschehen, auch um die sprachlichen Handlungen zu unterstützen. Auch sollte die Besprechung typischer Fehler (zum Beispiel beim Eintippen in den Taschenrechner) Bestandteil der Erstaneignung sein.
- Berechne das arithmetisches Mittel. Beschreibe anschließend dein Vorgehen.
Person A: a) 2; 4; 3; 7; 8; b) 2,5; 1,2; 5; 7,2
Person B: a) 5; 2; 8; 3; 4; b) 3,1; 1,2; 7; 4,8 - *Erkläre, welcher Fehler, beim Berechnen des arithmetischen Mittels der Datenreihe \(10; 17; 12; 13; 20\) gemacht wurde und korrigiere ihn. \[\bar{x} = 10+17+12+13+20:5 = 56\]
- Beschreibe, wie du beim Berechnen des arithmetischen Mittels mit dem Taschenrechner vorgehen kannst.
10.3.3 Festigung
Zur Festigung des arithmetischen Mittels bietet es sich an, Aufgaben vielfältig zu variieren (vgl. Abschnitt 9.1.3) und nach dem operativen Prinzip durchzuarbeiten.30
Speziell zum arithmetischen Mittel bietet Leuders (2009) hierzu eine reichhaltige Auswahl an Übungsaufgaben. Von denen müssen nun für die konkrete Unterrichtsstunde gezielt einige ausgesucht werden, ggf. auch mit Wahl- und Wahlpflichtcharakter für den differenzierenden Einsatz. Konkrete methodische Entscheidungen sind dann abhängig von der Lerngruppe zu treffen.
Sollte bereits andere Lagemaße behandelt worden sein, so bietet sich in einer Festigung auch immer ein Vergleich zwischen den Lagemaßen an. Das in Abbildung 10.3 dargestellte virtuelle Arbeitsmittel ermöglicht bspw. einen Vergleich zwischen Median und arithmetischem Mittel.
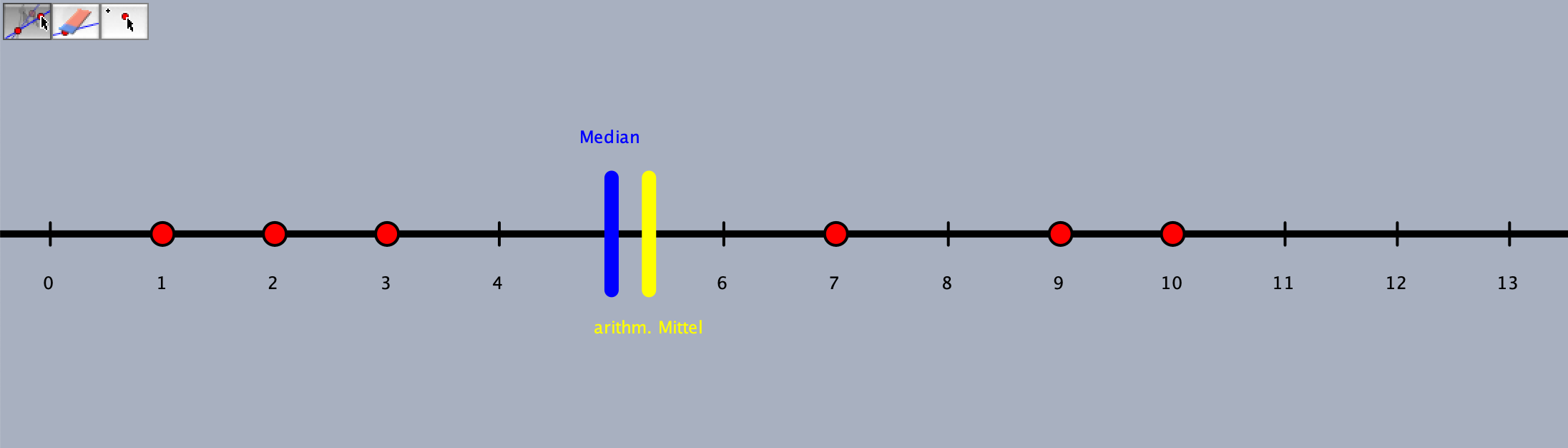
Abb. 10.3: Screenshot des virtuellen Arbeitsmittels zu Lagemaßen
Auf einer skalierten Achse sind dabei Punkte markiert und es wird das arithmetische Mittel (gelb) sowie der Median (blau) dargestellt. Die Punkte können verschoben werden und es ist möglich, neue Punkte hinzuzufügen bzw. existierende Punkte zu entfernen, wobei sich arithmetisches Mittel und Median automatisiert anpassen. Die folgenden Aufgabenstellungen zeigen exemplarisch, wie ein derartiges Arbeitsmittel genutzt werden kann, um Schülerinnen und Schüler zum operativen Durcharbeiten bezüglich dieser Lagemaße anzuregen:
- Verändere die Punkte so, dass Median und arithmetisches Mittel gleich sind.
- Kannst du Punkte verschieben, so dass Median oder arithmetisches Mittel unverändert bleiben? Bei welchen Punkten geht das (nicht) und warum (nicht)?
- Wie verändert sich das beobachtete Verhalten von arithmetischem Mittel und Median bei ungerader Anzahl an Punkten?
- Zeige mit dem Arbeitsmittel, dass der Median stabil gegenüber Ausreißern ist, das arithmetische Mittel jedoch nicht.
10.3.4 Handlungskontrolle
Die Beurteilung der erzielten Lernergebnisse kann, bei diesem relativ übersichtlichen Lerngegenstand, durch eine kleine Zusammenfassung am Ende der Unterrichtsstunde erfolgen. Um hierbei auch zu prüfen, ob die gewünschten Kompetenzziele erreicht worden sind, bieten sich folgende Impulse für kurzes Plenumsgespräch an:
- Fasse zusammen, was wir heute neues gelernt haben.
- Wofür benötigt man das arithmetische Mittel?
- Erkläre, wie man das arithmetische Mittel berechnet.
Dabei sollte auch noch einmal ein Bezug zu den ursprünglich formulierten Lernzielen erfolgen.
Abbildung 10.4 fasst die grundsätzliche Struktur der Unterrichtsstunde inkl. der ungefähren Zeitangabe der einzelnen noch einmal zusammen.

Abb. 10.4: Übersicht einer Unterrichtsstunde zum arithmetischen Mittel
10.4 Aufsteigen vom Abstrakten zum Konkreten
Das in Abschnitt ?? vorgestellt Vorgehen ist bezüglich der Begriffsbildung weder induktiv, noch deduktiv oder ostensiv. Es wird nicht von mehreren Beispiel heraus das Allgemeine generiert (induktiv) und auch nicht zunächst die Definition gegeben und daraufhin Beispiele generiert (deduktiv) und die Begriffseinführung erfolgt auch nicht nur rein erklärend anhand eines Beispiels (ostensiv). Vielmehr ist das Vorgehen aus einem Wechselspiel von einem Beispiel, der Definition und weiterer Beispiele gesprägt. In der dargestellten Form entspricht das Vorgehen dem sogenannten Aufsteigen vom Abstrakten zum Konkreten, welches nach Lompscher (1996) aus drei Schritten besteht.

Abb. 10.5: Aufsteigen vom Abstrakten zum Konkreten
Für die Einführung des Begriffs wird ein konkretes Ausgangsbeispiel gewählt, an dem das Wesen des Begriffs besonders gut deutlich wird. An diesem Ausgangskonkretum werden Lernhandlungen erarbeitet, die sich zwar am Beispiel orientieren, aber verallgemeinern lassen, sodass sie dem Begriffsaufbau dienlich sind.
Im obigen Beispiel war das der Vergleich der Leistungen von Luca und Alex, typische Lernhandlungen waren das Aneinanderlegen der Sprungweiten und anschließende Teilen.
Im Anschluss wird, mit Unterstützung der Lehrkraft, das Wesen des Begriffs herausgearbeitet und in Form einer Ausgangsabstraktion formuliert. Dieses Vorgehen ist vergleichbar mit dem induktiven Begriffserwerb, allerdings wird nicht aus einer Vielzahl von Beispielen eine gemeinsame Eigenschaft eliminiert, sondern am charakteristischen Beispiel wird die Eigenschaft durch eine wissende Person (Lehrkraft) in Bezug auf die Handlungserfahrungen der Schülerinnen und Schüler dargestellt. Dieser Prozess wird unterstützt mithilfe von Lernmodellen (vgl. Abschnitt 5.1.3), bspw. in Form von Arbeitsmitteln oder Orientierungshilfen.
Im obigen Beispiel kann die Pfeil-Repräsentation zur Vorstellung des arithmetischen Mittels als Wert einer gleichmäßigen Verteilung als solches Lernmodell aufgefasst werden.
Der dritte Schritt, das eigentliche Aufsteigen vom Abstrakten zum Konkreten, ist nun das Abarbeiten von Konkretisierungsreihen. Hierzu werden weitere Beispiele für den Begriff betrachtet, auf die das Ausgangsabstraktum angewandt wird. Das Lernmodell dient dabei als Mittler und die Lernhandlungen werden in verallgemeinerter und ggf. auch modifizierter Form angewandt. Erst auf diese Weise ist ein echtes Durchdringen des Begriffs möglich. Dieses Vorgehen ist mit dem deduktiven Vorgehen vergleichbar, allerdings nicht im dem Sinne, dass aus einer Definition heraus die Beispiele generiert werden. Vielmehr wird auf gegebene Beispiele die Definition angewandt, ausgeschärft und damit der Begriff immer besser verstanden.
Die Erstaneignungs- und Festigungsaufgaben im obigen Beispiel dienen damit als Konkretisierungsreihen.
Dies Vorgehensweise hat den Vorteil, relativ effektiv ist, trotz des Verzichts auf ein deduktives Vorgehen recht schnell zu einer (ersten) Definition des Begriff zu kommen. Außerdem ist sie ehrlich gegenüber den noch nicht vorhandenen Kenntnissen der Schülerinnne und Schüler gegenüber, da diese bei einem induktiven Vorgehen i. d. R. noch nicht wissen, nach welchem gemeinsamen Merkmal die Beispiele nun analysiert werden sollen, so dass es oft mit einem Raten (oder letztlich doch einer Vorgabe durch die Lehrkraft) verbunden ist, auf das zu interessierende Merkmal zu stoßen.
10.5 Zum Nachbereiten
Stellen Sie eine Sammlung geeigneter Übungsaufgaben für die Festigungsphase zum arithmetischen Mittel zusammen. Begründen Sie die Auswahl der Aufgaben mithilfe mathematikdidaktischer Theorien.
Diskutieren Sie, inwieweit die Theorie-Elemente der stoffdidaktischen Analyse (siehe auch Abschnitt 8.4) in den einzelenn Schritten des Aufsteigens vom Abstrakten zum Konkreten integriert werden können.
References
\(\sum\limits_{i=1}^n (x_i-\bar{x})^2 = \left(\sum\limits_{i=1}^nx_i^2\right)-n\bar{x}^2\)↩︎
Das ist auch der Grund, weshalb das arithmetische Mittel streng genommen nicht geeignet ist einen Notendurchschnitt zu bestimmen, da die Abstände zwischen den Notenstufen nicht gleich sind.↩︎
Es lohnt sich, an dieser Stelle noch einmal in die Vorlesungsunterlagen zur Einführung in die Mathematikdidaktik zu sehen.↩︎