9 Zweites Intermezzo: Ganze Zahlen
Ziele
- Sie vertiefen am Beispiel ganzer Zahlen Ihr Verständnis über den Vier-Ebenen-Ansatz, insbesondere wie aus den Ebenen heraus Rückschlüsse zum Aufbau eines Lernpfades entwickelt werden können.
Material
9.1 Stoffdidaktische Analyse
9.1.1 Formale Ebene
9.1.1.1 Natürliche Zahlen
Fachmathematisch können die ganzen Zahlen aus den natürlichen Zahlen generiert werden. Hierzu sollen zunächst die natürlichen Zahlen selbst fachmathematisch eingeordnet werden. Im Prinzip bestehen zwei Sichtweisen, nämlich die Einführung über die Peano-Axiome sowie die Betrachtung gleichmächtiger Mengen.
Aus den Peano-Axiomen (Wikipedia, 2021b) folgt zunächst die Existenz einer Reihenfolge von Zahlen (also Nachfolger der \(0\)), die dann mit \(1\), \(2\), \(3\) usw. bezeichnet werden können.21 Diese Bezeichnung erlaubt jedoch noch keinerlei Berechnungen, nicht einmal eine Ordnungsrelation ist vorhanden. Es kann also (noch) nicht gesagt werden, dass \(3\) größer ist als \(1\). Vielmehr lässt sich die Situation eher mit einem Alphabet vergleichen22, bei dem auch nicht C größer als A ist.
Für eine Ordnungsrelation bedarf es zunächst der Definition der Addition über \(n+0 := n\) und \(n+k' := (n+k)'\) für alle \(n,k\in\mathbb{N}\) mit der (aus den Peano-Axiomen existierenden) Nachfolgerbildung \('\). So gilt etwa mit \(1:=0'\): \({\color{blue} 1}+{\color{red} 1} = {\color{blue} 1}+{\color{red} {0'}} = ({\color{blue} 1}+{\color{red} 0}){\color{red} '} = 1{\color{red} '} =: 2\). So kann nun induktiv jede höhere Additionsaufgabe generiert werden. Darauf aufbauend kann die Ordnungsrelation \(n<m\) über die Existenz eines \(k\in\mathbb{N}\backslash\{0\}\) mit \(m = n+k\) definiert werden. Die Subtraktion \(m-n = k\) ist nun wiederum über die Umkehroperation \(n+k = m\) definierbar, sofern \(m\geq n\).
Die Gleichmächtigkeit (z. B. endlicher) Mengen \(M\) und \(N\) wird über die Existenz einer Bijektion zwischen diesen beiden Mengen definiert, siehe Abbildung 9.1.
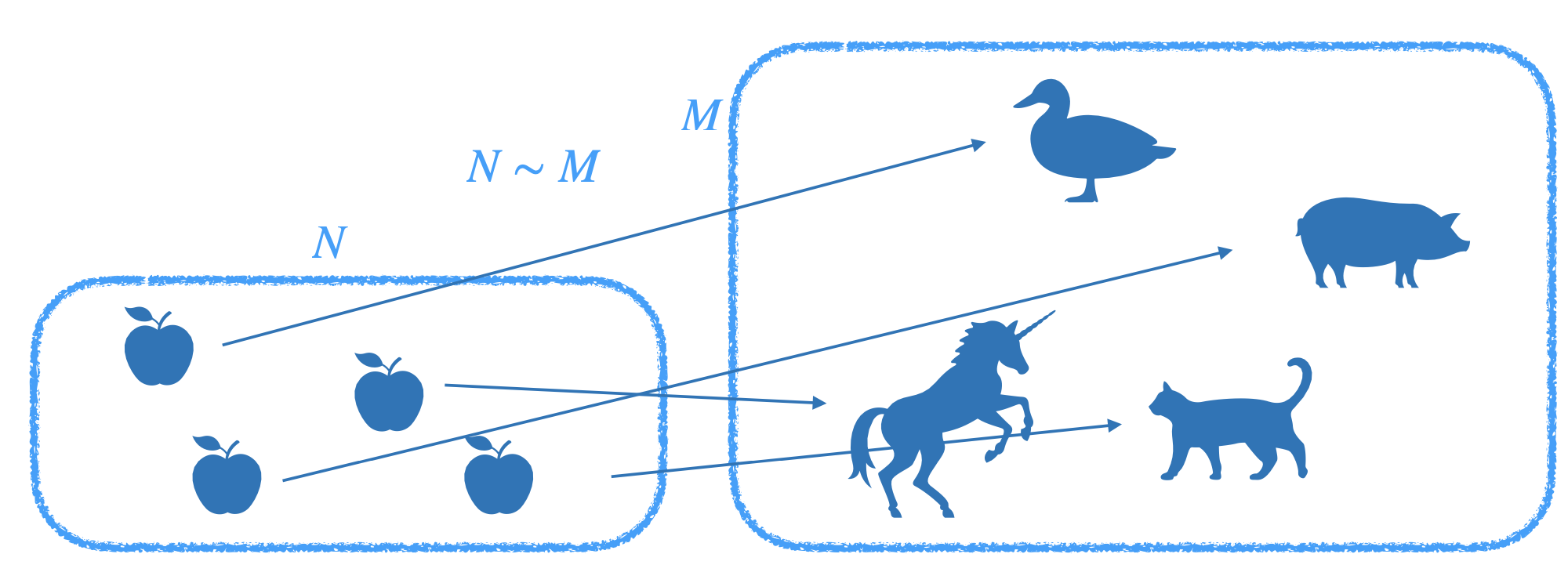
Abb. 9.1: Gleichmächtigkeit von Mengen
Diese Relation ist eine Äquivalenzrelation, also symmetrisch, reflexiv und transitiv. Damit können Äquivalenzklassen gebildet werden, die die Mächtigkeit der Menge angeben. Statt \([4]\) als Bezeichner für die Äquivalenzklasse von vierelementigen Mengen kann dann auch kurz die Zahl \(4\) genutzt werden. Die Addition \(n+k\) entspricht dann der Mächtigkeit der Vereinigungsmenge von \([n]\) und \([k]\), vgl. Abbildung 9.2.

Abb. 9.2: Additionsergebnis als Äquivalenzklasse der Vereinigungsmenge
9.1.1.2 Ganze Zahlen
Da innerhalb der natürlichen Zahlen noch nicht beliebig subtrahiert werden darf, stehen auch keine negativen Zahlen als Ergebnisse zur Verfügung. Um dennoch das Ergebnis bspw. der Aufgabe \(2-7\) »definieren« zu können, bietet sich erneut eine Äquivalenzrelation über die »Differenzengleichheit« an. Konkret lässt sich für \(k,l,m,n\in\mathbb{N}\) sagen: \((k,l)\sim (m,n):\Leftrightarrow k+n=l+m\) Das heißt z. B., dass die Zahlenpaare \((2,7)\), \((0,5)\) und \((4,9)\) in Relation zueinander stehen, weil sie dieselbe »Differenz« haben (obwohl es die Differenz formal noch nicht gibt). Dies ermöglicht nun die Einführung des Bezeichners \(-5\) für die Äquivalenzklasse \([(0,5)]\).
Das Vorgehen ist verträglich mit den bisherigen Regeln in \(\mathbb{N}\), d. h. es führt nicht zu Widersprüchen, wenn etwa das Zahlenpaar \((7,4)\) betrachtet wird mit dem Repräsentanten-Bezeichner \(3\). Die Menge aller Äquivalenzklassen (bzw. deren Kurzbezeichner) ist nun \(\mathbb{Z}\).
Die Addition und Subtraktion zweier Zahlenpaare sind nun definierbar:
\[\begin{align} (k, l) + (m, n) := (k + m, l + n)\\ (k, l) − (m, n) := (k, l) + (n, m) \end{align}\]
Als Alternative bietet sich ein axiomatisches Vorgehen an, also dass die ganzen Zahlen mit der Addition als abelsche Gruppe definiert werden – bedeutsam ist hier insbesondere die Existenz eines Inversen zu jeder Zahl.
Aus all den bisherigen Überlegungen auf der formalen Ebene lassen sich für den Unterricht zentrale Fachinhalte ableiten:
Ganze Zahlen können über Zahlenpaare aus den natürlichen Zahlen oder als »Gegenzahlen« der natürlichen Zahlen entwickelt werden.
- Natürliche Zahlen sind als Teilmenge in die ganzen Zahlen eingebettet.
- Die Subtraktion natürlicher Zahlen \(m-n\) mit \(n > m\) ist nun lösbar.
- Die Rechenregeln werden erweitert, wobei die bekannten weiter gelten.
9.1.2 Semantische Ebene
9.1.2.1 Grundvorstellungen
Die Einführung ganzer Zahlen ist für Schülerinnen und Schüler mit zahlreichen Schwierigkeiten verbunden (vom Hofe & Hattermann, 2014). Diese sind eigentlich auf der empirischen Ebene der stoffdidaktischen Analyse angesiedelt (mehr dazu siehe auch Abschnitt 9.1.4), sollen aber hier wegen ihrer Nähe zu den Grundvorstellungen schon einmal erwähnt werden.
- So bestehen etwa für das Minus-Zeichen vielfältige Interpretationsmöglichkeiten als Vorzeichen (z. B. in der Rechnung \(-5+2\)), als Rechenzeichen (z. B. in der Rechnung \(7-2\)) oder als Inversionszeichen (z. B. bei der Darstellung \(-a\) als Gegenzahl für \(a\)).
- Der in den natürlichen Zahlen vorhandene Kardinalzahlaspekt (dass die Zahl die Mächtigkeit einer Menge angibt), ist in den negativen Zahlen nicht mehr tragfähig (es existiert keine \(-4\)-elementige Menge). Auch der Ordinalzahlaspekt (dass die Zahl eine Position angibt) ist nur eingeschränkt tragfähig (eine \(-4\)-te Position bedarf vielfältiger Zwischeninterpretationen). Der Maßzahlaspekt (z. B. über die Angabe einer Zahl auf dem Zahlenstrahl) dagegen ist auf die ganzen Zahlen erweiterbar.
- Die Ordnungsrelation wird häufig fehlinterpretiert über eine spiegelbildliche Interpretation (z. B. kann fälschlicherweise \(-5>-3\) angenommen werden). Eine Ursache kann hier darin liegen, dass die Ordnungsrelation zuvor über die Mächtigkeit von Mengen hergestellt wurde, was nun nicht mehr möglich ist.
Gegenüber den natürlichen Zahlen sind also im Umgang mit (negativen) ganzen Zahlen einige Grundvorstellungsumbrüche zu absolvieren. Als normativ auszubildende Grundvorstellungen fassen vom Hofe & Hattermann (2014) zusammen:
- Ganze Zahlen als relative Zahlen bezüglich einer fest gewählten Vergleichsmarke: Dies ist etwa bei Etagen-Angaben, Temperaturen oder der Position über/unter dem Wasserspiegel der Fall. Gerade bei Temperaturen kann die Beliebigkeit der Vergleichsmarke (0 °C) gut diskutiert werden, da etwa andere Temperaturskalen (°F, K) eine andere Vergleichsmarke gewählt haben.
- Ganze Zahlen als Gegensätze: Diese Vorstellung wird z. B. sichtbar, wenn über Guthaben und Schulden gesprochen wird. Hat man 5 € Schulden, so ist dies der Gegensatz von 5 € Guthaben. Die Vergleichsmarke (0 €) ist hier nicht beliebig gewählt, sondern natürlicherweise über »weder Guthaben noch Schulden« gegeben. Auch der Betrag einer Zahl kann in dieser Vorstellung besonders gut verstanden werden.
- Ganze Zahlen als Richtungen: Negative Zahlen beschreiben in dieser Vorstellung die entgegengesetzte Richtung der positiven Zahlen. Dies ist z. B. bei der Verwendung von Koordinatensystemen der Fall, oder ganz allgemein bei der Zahlengeraden.
- Ganze Zahlen als Zustände und Zustandsänderungen: In dieser Vorstellung bieten ganze Zahlen nicht nur die Möglichkeit, einen Zustand (wie Guthaben oder Schulden) zu beschreiben, sondern auch den Prozess der Änderung dieser Zustände (Erhalt von Guthaben, Erlass von Schulden, …). Eine solche Vorstellung etwa ist nötig, um die verschiedenen Interpretationen des Minus-Zeichens nachvollziehen zu können.
Als bedeutsamste Repräsentation negativer Zahlen gilt die Zahlengerade. Diese stützt einerseits den Maßzahlaspekt und ermöglicht über die Darstellung von Punkten und Pfeilen (siehe Abbildung 9.3) auch eine Interpretation in den verschiedenen Grundvorstellungen.
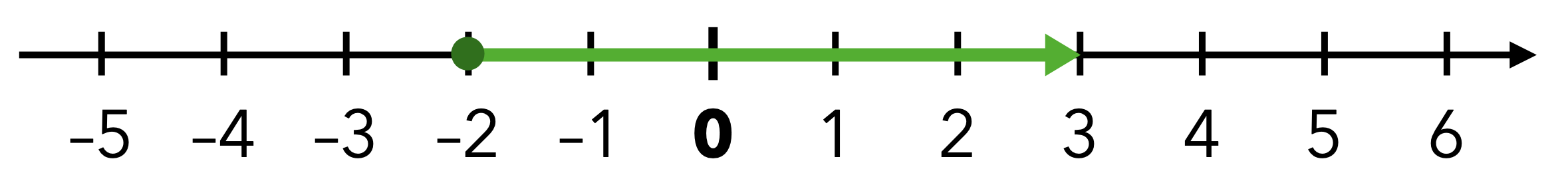
Abb. 9.3: Zahlengerade
Auch Operationen mit ganzen Zahlen sind hierzu nun verständlich behandelbar:
- So kann das Addieren/Subtrahieren als Anlegen von Pfeilen, gerichtetes Weiter-/Zurückzählen oder als Subtraktion/Addition der Gegenzahl aufgefasst werden.
- Das Multiplizieren kann bei der Multiplikation mit einer positiven Zahl als Streckung/Stauchung aufgefasst werden, die Multiplikation mit \(-1\) entspricht der Spiegelung an der Null und die Multiplikation mit einer beliebigen negativen Zahl ist eine Kombination aus beidem.
- Der Größenvergleich ist nun über einen Lagevergleich auf der Zahlengeraden möglich, wobei weiter links liegende Zahlen immer kleiner sind als weiter rechts liegende.
9.1.2.2 Fundamentale Ideen
Hinsichtlich des Katalogs an Tätigkeitsideen (siehe Abschnitt 2.2.1.3) besteht die Möglichkeit, ganze Zahlen als Verallgemeinerung oder Vernetzung aufzufassen. Sinnvoller erscheint mir jedoch, von einer Erweiterung zu sprechen – nicht im Sinne des Erweiterns von Brüchen, sondern der Zahlbereichserweiterung und in dem Zusammenhang auch einer Erweiterung der nötigen Rechenregeln. Auch Freudenthal (1989, S. 27) spricht von der »Idee der Erweiterung unter Aufrechterhaltung gewisser Gesetze«. Auf eine ausführliche Darstellung der Kriterien fundamentaler Ideen wird hier verzichtet – als Ausblick auf das Vertikalkriterium sei nur auf andere Erweiterungssituationen des Mathematikunterrichts verwiesen wie die sonstigen Zahlbereichserweiterungen, die Übertragung der Potenzgesetze auf rationale Exponenten oder eine Herleitung, dass \(a^0 = 1\) und \(0^0\) nicht definiert ist.
Ein typisches Erweiterungsbeispiel im Zusammenhang mit ganzen Zahlen ist die Multiplikation zweier negativer Zahlen. Kann die Multiplikation einer natürlichen Zahl (erster Summand) mit einer negativen Zahl (zweiter Summand) außermathematisch noch als mehrfache Verschuldung aufgefasst und die Vertauschung von erstem und zweitem Summanden über das Kommutativgesetz innermathematisch erklärt werden, bietet die Multiplikation zweier negativer Zahlen keine so naheliegende Interpretation. Abhilfe schafft hier das Permanenzprinzip, nach dem neue Theorien (z. B. das Rechnen mit negativen Zahlen) soweit wie möglich verträglich sein muss mit bisherigen Theorien (z. B. das Rechnen mit positiven Zahlen). Sichtbar gemacht werden kann dieses Prinzip und die Herleitung gewisser Rechenregeln über Permanenzreihen. Abbildung 9.4 stellt dies am Beispiel der Aufgabe \((-3)\cdot (-5)\) dar.
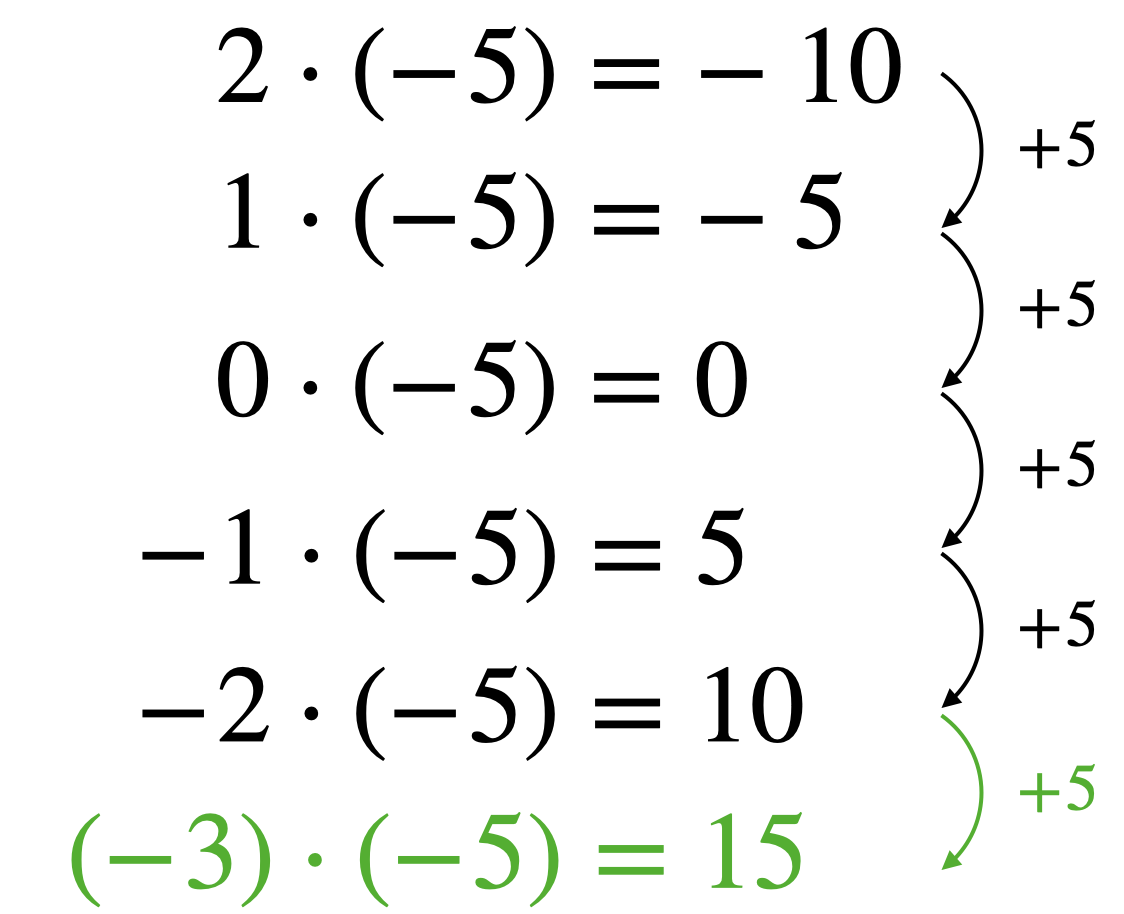
Abb. 9.4: Permanenzreihe zur Multiplikation zweier negativer Zahlen
Zusammenfassend lassen sich auf der semantischen Ebene folgende für den Lernpfad relevanten Zusammenhänge ableiten:
- Ganze Zahlen sollten als relative Zahlen bezüglich einer fest gewählten Vergleichsmarke, als Gegensätze, als Richtungen sowie als Zustände und Zustandsänderungen aufgefasst werden können
- Die Zahlengerade ist eine wesentliche Repräsentation ganzer Zahlen, anhand derer auch die Operationen mit ganzen Zahlen sichtbar gemacht werden können.
- Die Einführung ganzer Zahlen soll über das Permanenzprinzip begleitet werden, bei der Herleitung von Rechenregeln bietet sich die Nutzung von Permanenzreihen an.
9.1.3 Konkrete Ebene
Aus den Überlegungen auf der formalen und semantischen Ebene kann als mathematischer Kern der Betrachtung ganzer Zahlen herausgearbeitet werden, dass mit diesen nun stets subtrahiert werden kann (als Neuheit gegenüber den natürlichen Zahlen) und dass in ihnen spezifische Rechenregeln gelten, die so zuvor nicht bekannt waren. Als Kernfragen formuliert, kann dies heißen (vgl. Leuders et al., 2015, S. 80, 82):
- »Wie kann man rechnen, wenn man mehr wegnimmt, als man hat?«
- »Wie kann man mit negativen Zahlen wiederholt dasselbe rechnen?«
Bei der Wahl eines geeigneten Kontextes besteht die Herausforderung, dass die Zahlen und Rechnungen eine Relevanz im Kontext haben und nicht nur konstruiert sind. In der zunächst naheliegenden Temperaturbetrachtung bestehen einige physikalische Schwierigkeiten, nämlich dass auf der Celsius-Skala Temperaturen stets Zustände und keine Zustandsänderungen beschreiben (letztere werden in Kelvin angeben). Auch die Existenz eines absoluten Nullpunkts (\(-273,\!15\,°\mathrm{C}\)) widerspricht der mathematischen Betrachtung beliebig kleiner negativer Zahlen. Hinzu kommt, dass die Gegensatz-Vorstellung keine praktische Bedeutung hat: \(-2\,°\mathrm{C}\) ist nicht das Gegenteil von \(2\,°\mathrm{C}\).
Wie schon die Beispiele zu den Grundvorstellungen in Abschnitt 9.1.2.1 gezeigt haben, bietet dagegen das Guthaben-Schulden-Modell vielfältige sinnstiftende (also lebensweltbezogene, kontextauthentische und reichhaltige) Anknüpfungspunkte. Eingeführt werden kann dieser Kontext z. B. spielerisch über Guthaben- und Schuldenkarten, wobei Würfel dafür eingesetzt werden können, wie viele Guthaben- oder Schuldenkarten man abgeben muss bzw. erhält. Über die Dokumentation von »Kontoständen und -bewegungen« kann der Prozess festgehalten werden. Weitere Anregungen zu diesem Kontext findet man auch bei Hattermann et al. (2014) sowie Hußmann & Schindler (2014).
Während sich aus dem Kontext heraus Additions- und Subtraktionsaufgaben beschreiben lassen, bei denen die zweite Zahl positiv ist (was einer horizontalen Mathematisierung entspricht), sind derartige Aufgaben mit negativer zweiter Zahl besser über Pfeile auf Zahlengeraden zu veranschaulichen. Dabei kann das Rechenzeichen als Blick- (\(+\) rechts, \(-\) links) und das Vorzeichen der zweiten Zahl als Bewegungsrichtung (\(+\) vorwärts, \(-\) rückwärts) aufgefasst werden. Dieses Vorgehen bietet jedoch keine innermathematische Erklärung, vielmehr ist dies eher eine Art Eselbrücke. Eine vertikale Mathematisierung wird dann insbesondere bei der innermathematischen Erklärung von Multiplikationsaufgaben relevant. Abbildung 9.5 zeigt noch einmal die verschiedenen Mathematisierungsarten.

Abb. 9.5: Horizontale (h) und vertikale (v) Mathematisierungsmöglichkeiten bei ganzen Zahlen
Zusammenfassend lässt sich sagen:
- Über den Kontext von Guthaben-Schulden-Situationen lässt sich das Wesen ganzer Zahlen erarbeiten.
- Als Kernideen sollten deutlich werden, dass man mit ganzen Zahlen beschreiben kann, wie man mehr wegnehmen kann, als man hat, und dass mit ihnen die bekannten Rechengesetze erweitert werden.
- Im Guthaben-Schulden-Kontext lassen sich einige der Rechengesetze veranschaulichen, andere wiederum können über Permanenzreihen erklärt werden.
9.1.4 Empirische Ebene
Neben den bereits in Abschnitt 9.1.2.1 erwähnten typischen Schwierigkeiten mit ganzen Zahln, sollen hier noch einige weitere aufgezählt und ihre Konsequenzen für die Entwicklung eines Lernpfades abgeleitet werden.
- Die Einführung negativer Zahlen ist für Schülerinnen und Schüler mit hohen sprachlichen Hürden verbunden (siehe z. B. Fabian, 2022). Dies betrifft einmal den negativ-Begriff, der in der Alltagssprache i. d. R. mit etwas schlechtem verbunden ist (»negative Stimmung«), aber auch eine positive Bedeutung haben kann (»negativer Corona-Test«), im mathematischen Kontext jedoch bei der »negativen Zahl« eine gänzlich andere Bedeutung hat. Diese Bedeutungsvielfalt sollte daher im Unterricht angesprochen und die mathematische Bedeutung entsprechend abgegrenzt werden. Eine weitere Hürde ist ein komplexer Wortschatzaufbau, abhängig von den verwendeten Kontexten. So muss nicht nur der neue mathematische Inhalt erlernt, sondern es müssen in dem Zusammenhang auch noch die verwendeten Wörter wie »Meeresspiegel«, »Normal-Null«, »Gefrierpunkt«, »Frost« usw. mit ihrer mathematischen Bedeutung hinsichtlich der positiven und negativen Zahlen in Bezug gebracht werden. Dieses Problem lässt sich umgehen, indem die Einführung möglichst nur in einem Kontext erfolgt und dieser nur geringe sprachliche Hürden aufweist.
- Aus den natürlichen Zahlen herrscht die Vorstellung vor, dass Hinzufügen, also (ggf. mehrfaches) Addieren, immer vermehre. Diese »Hinzufügen vemehrt immer«-Vorstellung ist jedoch nicht mehr tragfähig. Ihre Ursache hat die Vorstellung aus einer jahrelangen Betrachtung ausschließlich positiver Zahlen und wird teils auch sprachlich gestützt (z. B. durch »noch mehr Schulden«). Einer entsprechenden Übergeneralisierung muss also durch einen verständnisfördernden Aufbau entgegengewirkt werden, ggf. auch mit einer expliziten Besprechung der Fehlvorstellung.
- Ebenfalls sichtbar wird eine Häufige Vermischung der Rechenregeln, z. B. die fehlerhafte Aussage »minus plus minus ist plus«, die aus einer Übertragung der Merkregel »minus mal minus ist plus« kommen könnte. Eine solche Vermischung kommt inbesondere dann zutage, wenn die Rechenregeln (falsch) auswendig gelernt und nicht mit einer geeigneten Vorstellung in Bezug gebracht werden können. Für die Unterrichtsdurchführung bedeutet das, dass die entsprechenden Repräsentationen (wie Pfeile am Zahlenstrahl) behutsam eingeführt, ausführlich behandelt sowie durch operatives Durcharbeiten verinnerlicht werden sollten. Auch der Verzicht auf Merksätze kann hierbei tatsächlich hilfreich sein, um nicht auf solch ein kalkülhaftes Vorgehen (welches sich dann falsch eingeprägt wird) hinzuwirken.
9.2 Lernpfad
Aus den Überlegungen der stoffdidaktischen Analyse lässt sich nun ein möglicher Lernpfad ableiten, nach dem ganze Zahlen unterrichtet werden können. Abbildung 9.6 stellt diesen übersichtlich dar.
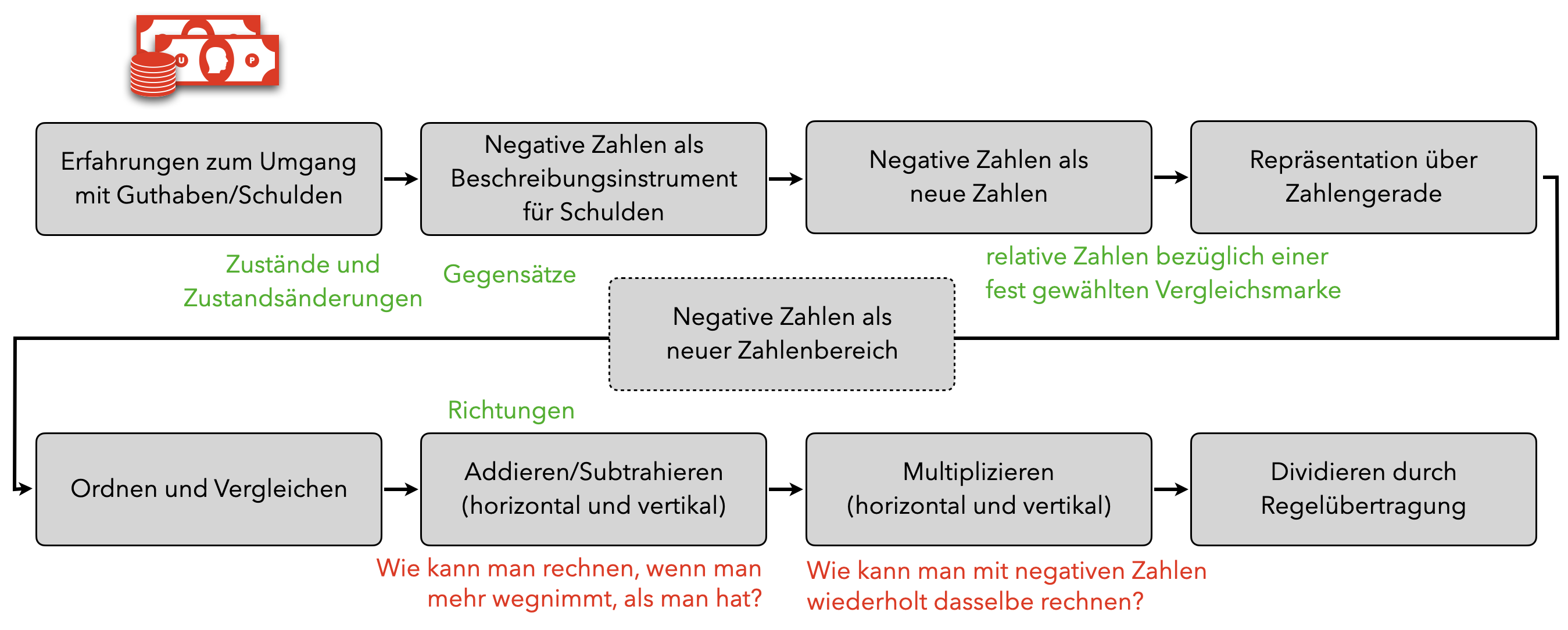
Abb. 9.6: Möglicher Lernpfad zu ganzen Zahlen
Dabei zeigt sich, dass in der oberen Zeile zunächst die Zahlen als Objekte betrachtet werden, wobei schon vielfältige Grundvorstellungen aufgebaut werden können. Der komplette Lernpfad lässt sich dabei am Guthaben-Schulden-Modell durcharbeiten, wobei natürlich in Anwendungsituationen und zur Verinnerlichung auch weitere Kontexte nötig werden.
Die Einführung des Zahlbereichs \(\mathbb{Z}\) ist in der Darstellung gestrichelt dargestellt, da dieser nicht zwingend an der Stelle nötig ist, um anschließend mit ganzen Zahlen rechnen zu können. Hier kann auch die Leistungsfähigkeit der Klasse sowie die Schuform darüber entscheiden, ob und an welcher Stelle der Zahlbereich als Begriff eingeführt werden muss.
Die untere Zeile beschäftigt sich nun mit dem Operieren mit ganzen Zahlen, v. a. an der Repräsentation der Zahlengeraden. Dabei werden nun die Kernfragen (bzw. deren Beantwortung) besonders deutlich und die Richtungsvorstellung erhält eine größere Bedeutung.
Dieser Lernpfad stellt eine Möglichkeit dar, ganze Zahlen zu behandeln und baut auf die obigen Diskussionen zur formalen, semantischen, konkreten und empirischen Ebene auf. Damit allein jedoch ist noch kein Unterricht möglich! Eine konkrete Unterrichtsplanung kann nun erst, auf den Lernpfad aufbauend, begonnen werden. Abhängig von der Klasse und anderen äußeren Bedingungen (»Bedingungsanalyse«) sind nun geeignete Aufgabenstellungen und Arbeitsmittel auszuwählen, methodisch in Lernumgebungen zu integrieren und damit konkrete Stundenplanungen zu entwickeln.