13 Leitidee Strukturen und funktionaler Zusammenhang
Material
Literaturempfehlungen
- Greefrath et al. (2016): Didaktik der Analysis. Aspekte und Grundvorstellungen zentraler Begriffe
- Danckwerts & Vogel (2010): Analysis verständlich unterrichten
- Weigand et al. (2022): Didaktik der Algebra: nach der Vorlage von Hans-Joachim Vollrath
- Tietze et al. (2000a): Mathematikunterricht in der Sekundarstufe II. Band 1: Fachdidaktische Grundfragen, Didaktik der Analysis
13.1 Strukturierung der Leitidee
| Dokument | Bezeichnung der Leitidee |
|---|---|
| Bildungsstandards Primarbereich (2005) | Muster und Strukturen |
| Bildungsstandards Primarbereich (2022) | Muster, Strukturen, funktionaler Zusammenhang31 |
| Bildungsstandards Mittlerer Schulabschluss (2004) | Funktionaler Zusammenhang |
| Bildungsstandards Erster und Mittlerer Schulabschluss (2022) | Strukturen und funktionaler Zusammenhang |
| Rahmenlehrplan Brandenburg, Jahrgangsstufen 1 – 10 | Gleichungen und Funktionen |
| Bildungsstandards Allgemeine Hochschulreife (2012) | Funktionaler Zusammenhang |
| Rahmenlehrplan Brandenburg, Gymnasiale Oberstufe | Funktionaler Zusammenhang |
Abbildung 13.1 zeigt das vom LISUM (o. J.-d) für die Jahrgangsstufen 1 – 10 herausgegebene Konzeptbild zur Leitidee Strukturen und Funktionaler Zusammenhang, ergänzt durch einen didaktischen Kommentar von Kortenkamp & Kuzle (o. J.-b) und Materialien zur Diagnose und Förderung (LISUM, o. J.-c).
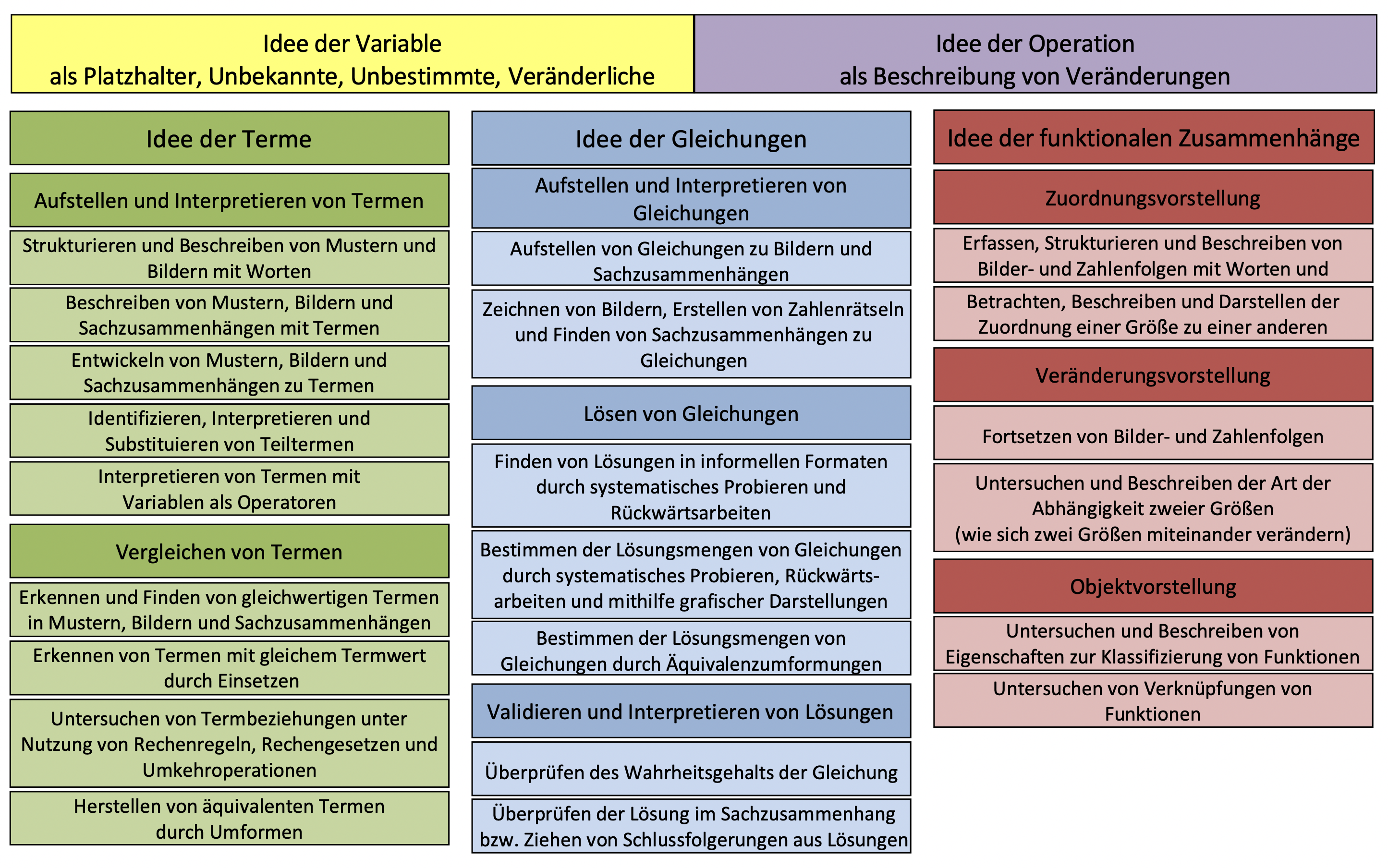
Abb. 13.1: Konzeptbild zur Leitidee Gleichungen und Funktionen (LISUM, o. J.-d)
Daraus sowie mit den Beschreibungen in den Bildungsstandards für die Sekundarstufen (Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, 2012, 20; 2022a, 18 f.) können folgende Lerngegenstände als bedeutsam angesehen werden:
Bedeutsame Lerngegenstände
- Variablen
- Terme
- Wachstumsprozesse
- Maßstäbe
- Darstellungformen funktionaler Zusammenhänge (sprachlich, tabellarisch, grafisch, algebraisch)
- proportionalen und antiproportionalen Zuordnungen, Dreisatz
- lineare und quadratische Gleichungen
- lineare Gleichungssysteme
- Lösbarkeit und der Lösungsvielfalt von linearen und quadratischen Gleichungen sowie linearen Gleichungssystemen
- Merkmale von Funktionen aus Funktionsterm, Graph und Wertetabelle
- lineare Funktionen
- quadratische Funktionen
- Exponentialfunktionen
- Logarithmusfunktion
- Sinusfunktion
- Verknüpfungen und Verkettungen von Funktionen
- Ableitung und Ableitungsfunktion
- Ableitungsregeln
- Monotonie und Extrema
- Bestimmtes Integral
- Hauptsatz der Differenzial- und Integralrechnung
- Stammfunktionen
- Zufallsgrößen und Wahrscheinlichkeitsverteilungen
Im Folgenden werden kurz Grundvorstellungen zum Variablen- und zum Funktionenbegriff vorgestellt, bevor dann näher auf die Analyses der Sekundarstufe II, insbesondere hinsichtlich den Ableitungsbegriffs, eingegangen wird.
13.2 Variablenaspekte
Gemäß der in Kapitel 3 eingeführten Bezeichnungen können zu drei Grundvorstellungen des Variablenbegriffs Aspekte formuliert werden, hier entnommen aus Weigand et al. (2022, 35 f.)
Grundvorstellung zum Aspekt als Unbekannte: »Die Variable ist ein Platzhalter für eine Zahl, deren Wert nicht bekannt ist, aber prinzipiell bestimmt werden kann, etwa durch regelgeleitete Umformungen.«
Diese Vorstellung ist i. d. R. die zuerst vorkommente Vorstellung zum Variablenbegriff in der Schullaufbahn. Betrachtet man etwa die Gleichung \(x+5 = 15\), so ist die Variable \(x\) zunächst unbekannt, kann aber hier bestimmt werden mit \(x = 10\). In der Grundschuldidaktik Mathematik taucht auch der Begriff Platzhalteraspekt auf, der einer Variablen zugeschrieben wird (siehe auch Abbildung 13.1). Dies wird etwa in Aufgaben der Art \(2 + \square = 7\) sichtbar. Im Platzhalteraspekt hat die Variable jedoch noch nicht die Funktion eines eigenständigen mathematischen Objektes – den erhält sie erst im Unbekanntenaspekt. Im dem Sinne befindet man sich hier also gerade im Übergang von der Arithmetik zur Algebra (vgl. Weigand et al., 2022, 39 ff.).
Grundvorstellung zum Aspekt als Unbestimmte bzw. allgemeine Zahl: »Die Variable ist eine allgemeine Zahl, deren Wert nicht gegeben ist bzw. zunächst nicht von Interesse ist.«
Wird etwa die Flächeninhaltsformel eines Rechteckts mit \(A = a\cdot b\) angegeben, so ist bspw. \(a\) eine Variable, deren Größe nicht interessiert (solange keine konkrete Berechnung angestellt wird). Relevant ist nur, dass \(a\) hier für die Länge einer Rechtseckseite steht.
Grundvorstellung zum Aspekt Veränderliche: »Die Variable ist eine Zahl oder Größe, die verschiedene Werte aus einem festgelegten Bereich annehmen kann, also veränderlich ist.«
Dieser Aspekt ist insbesondere bei der Betrachtung von Funktionen relevant. In der Gleichung \(y = 2x+5\) etwa steht die Variable \(x\) für eine Zahl (aus \(\mathbb{R)}\)), die verändert werden kann (woraufhin ihr Einfluss auf \(y\) betrachtet wird.)
Alle drei Aspekte sind notwendig, um mathematische Fragestellungen zu lösen. Betrachtet man etwa die Flächeninhaltsformel \(A = \frac{1}{2}ah\) für ein Dreieck mit Grundseite \(a\) und Höhe \(h\), ermöglichen die Aspekte, folgende Zusammenhänge zu verstehen (vgl. Barzel & Holzäpfel, 2011, S. 4):
- Unbekannte: Wie groß ist \(h\) für \(A= 20\,\mathrm{cm}^2\) und \(a = 5\,\mathrm{cm}\)?
- Unbestimmte: Zur Berechnung des Flächeninhalts muss ich \(h\) einsetzen.
- Veränderliche: Wie ändert sich der Flächeninhalt, wenn ich \(h\) verdopple?
Inwiefern die hier genannten Aspekte einen Einfluss darauf haben, welche mathematischen Handlungen nun mit Variablen möglich sind (wie etwa Einsetzen, Beschreiben eines Zusammenhangs, …), wird bei Weigand et al. (2022, S. 42) dargestellt.32
Hinweise zum Formelsatz im Zusammenhang mit Variablen, was für Sie inbesondere bei der Gestaltung von Arbeitsblättern von Relevanz sein kann, finden sich unter Wikipedia (2022a).
13.3 Funktionsaspekte
Dreh- und Angelpunkt der Leitidee Funktionaler Zusammenhang und damit auch des Stoffgebiets Analysis ist der Funktionsbegriff. Die hier formulieren Funktionsaspekte sind entnommen aus Greefrath et al. (2016, 47 ff.)33:
Grundvorstellung zum Zuordnungsaspekt: »Eine Funktion ordnet jedem Wert einer Größe genau einen Wert einer zweiten Größe zu. Mit dem Mengenbegriff formuliert bedeutet dies: Eine Funktion ordnet jedem Element einer Definitionsmenge genau ein Element einer Zielmenge zu.«
Typische Repräsentationen dieser Vorstellung sind Wertetabellen oder Pfeildiagramme. Über die (nicht-)Eindeutigkeit abgehender und ankommender Pfeile in der Definitions- und Zielmenge kann bspw. operativ an Beispielen diskutiert werden, ob eine Funktion vorliegt oder nicht. Die einführende Definition des formalen Funktionsbegriffs (meist in Klassenstufe 8) erfolgt in der Regel über den Zuordnungsaspekt – was die Gefahr einer einseitigen Betrachtung des Begriffs mit sich bringt. Sie müssen sich als Lehrkraft also zunächst einmal der Aspektvielfalt bewusst sein und diese dann auch bei Ihrer Unterrichtsgestaltung beachten.
Grundvorstellung zum Kovariationsaspekt/Änderungsaspekt: »Mit Funktionen wird erfasst, wie sich Änderungen einer Größe auf eine zweite Größe auswirken bzw. wie die zweite Größe durch die erste beeinflusst wird.«
Ohne den Kovariationsaspekt ist kein inhaltliches Verständnis von Differenzialrechnung möglich, da der Ableitungsbegriff ja gerade die lokale Änderung einer Funktion beschreibt. Aber auch in der Sekundarstufe I spielt dieser Aspekt schon eine bedeutsame Rolle, bspw. bei der Betrachtung proportionaler Zuordnungen als gleichmäßige Zunahme oder wenn unterschiedlich steile lineare Funktionen und das entsprechende Anstiegsdreick behandelt werden.
Grundvorstellung zum Objektaspekt: »Eine Funktion ist ein einziges Objekt, das einen Zusammenhang als Ganzes beschreibt.«
Insbesondere bei der Betrachtung von Funktionsgraphen wird ein solcher Gesamtblick geschult und die Funktion als Objekt aufgefasst. Der Objektaspekt ist u. a. auch bei der Betrachtung des Parametereinflusses von Relevanz, da dort die Funktion als Ganzes manipuliert wird. Algebraisch spielt der Aspekt eine Rolle, wenn Funktionsterme addiert werden oder Funktionen bspw. als Elemente eines Vektorraumes aufgefasst werden.
13.4 Analysis in der Sek. II
13.4.1 Konflikt zur Fachmathematik
Der Analysisunterricht in der Schule unterscheidet sich wesentlich von dem in der Hochschule, womit aus fachlicher wie fachdidaktischer Sicht einige Herausforderungen einhergehen. Neben der grundsätzlichen nicht streng deduktiven Herangehensweise werden i. d. R. zentrale Begriffe der Analysis im Schulunterricht kaum oder nur propädeutisch-anschaulich behandelt. Die betrifft zunächst einmal den Folgen-, Grenzwert- und Stetigkeitsbegriff (Danckwerts & Vogel, 2010, 17 ff.; Greefrath et al., 2016, 23 ff.; Tietze et al., 2000a, 252 ff.). Der Ableitungsbegriff bedarf bspw. des Grenzwertes des Differenzenquotienten. Ein solcher Grenzwert einer Funktion \(f\) an einer Stelle \(a\) existiert, wenn für alle Folgen \((x_n)_{n\in\mathbb{N}}\) mit \(x_n\rightarrow a\) auch die Folge der Funktionswerte konvergiert, also \(f(x_n)\rightarrow f(a)\). Für den Konvergenzbegriff einer Folge ist nun zum anderen die Vollständigkeit der reellen Zahlen von enormer Bedeutung, was ebenfalls in der Schule nicht in einer derartigen Strenge behandelt wird (siehe z. B. Danckwerts & Vogel, 2010, 27 ff.). Mathematisch relevant ist für die Konvergenz einer Folge \((x_n)_{n\in\mathbb{N}}\) gegen \(a\) eben nicht nur, dass die Folgenglieder dem \(a\) beliebig nahe kommen, sondern dass \(a\) im betrachteten Zahlbereich tatsächlich existiert. Ein klassisches Beispiel hierfür ist das Heronverfahren zum Wurzelbestimmen. So liefert die rekursive Folge34 \(x_{n+1} = \frac{1}{2}\left(x_n + \frac{5}{x_n}\right)\) mit bspw. \(x_0 = 1\) ausschließlich Folgenglieder aus \(\mathbb{Q}\), die sich auch beliebig nahe kommen (eine sogenannte Cauchy-Folge), der Grenzwert selbst ist aber \(\sqrt{5}\), was nicht in \(\mathbb{Q}\), sondern nur in \(\mathbb{R}\) liegt.
Ohne derartige zentrale (im fachmathematischen Sinne sauber ausgeprägte) Begriffe Analysisunterricht zu betreiben, bedarf also einer starken Orientierung an den hinter den Begriffen liegenden Grundvorstellungen, damit dennoch ein inhaltlich-anschauliches Verständnis aufgebaut werden kann und der Unterricht nicht zu einem kalkülhaften Vorgehen verkommt. Spezifische Anregungen für einzelne Lerngegenstände bieten die bereits zitierten Quellen.
13.4.2 Beispiel Ableitungsbegriff
Für den Ableitungsbegriff (einer Funktion an einer Stelle) haben sich sowohl historisch als auch in der fachdidaktischen Literatur zwei wesentliche Vorstellungen herausgebildet (Danckwerts & Vogel, 2010, 45 ff.; Greefrath et al., 2016, 147 ff.):
Grundvorstellung zum Aspekt der lokalen Änderungsrate: Die Ableitung einer Funktion an einer Stelle beschreibt, wie stark sich die Funktionswerte in der Umgebung dieser Stelle verändern. Wird sich dieser Änderungsrate graphisch genähert, erfolgt dies i. d. R. durch den Übergang des Anstiegs einer Sekante zu dem einer Tangente35, womit die Ableitung über den Grenzwert des Differenzenquotienten \(\lim\limits_{h\rightarrow 0}\cfrac{f(x_0+h)-f(x_0)}{h}\) quantifiziert werden kann und dem Anstieg der Tangente entspricht.
Diese Sichtweise ermöglicht, den Ableitungbegriff konstruktiv über den Sekanten-Tangenten-Übergang einzuführen und unmittelbar numerisch zu beschreiben. Auch bedienen sich vielfältige Anwendungen (z. B. Momentan- vs. Durchschnittsgeschwindigkeit) dieser Vorstellung.
Grundvorstellung zum Aspekt der lokalen Linearität: Diese Vorstellung betont noch stärker die Differenzierbarkeit als Eigenschaft einer Funktion, nämlich die Möglichkeit, sie lokal durch eine lineare Funktion annähern zu können. Eine typische Repräsentation ist das Heranzoomen an die Funktion, sodass dabei die lokale Linearität besonders deutlich wird. Mathematisch greifbar wird diese Vorstellung darüber, dass sich die Funktion über \(f(x) = f(x_0) + m\cdot x+ r(h)\) beschreiben lässt, wobei der Fehler \(r(h)\) so schnell gegen \(0\) geht, dass sogar \(\lim\limits_{h\rightarrow 0}\cfrac{r(h)}{h}=0\) gilt. \(m\) selbst ist dann die Ableitung und der Anstieg der besten linearen Näherung – was natürlich wieder die Tangente an entsprechender Stelle ist.
Dieses Vorgehen besticht v. a. durch seine mathematische Verallgemeinerbarkeit für die höherdimensionale Analysis. Auch entspricht es dem Bedürfnis, Prozesse linear zu approximieren (vgl. Abschnitt 2.2.2).
References
Die Leitidee dient hier als Hintergrund-Leitidee hinter den anderen, vgl. Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland (2022b, S. 6).↩︎
Die Begrifflichkeiten zu Aspekten und Grundvorstellungen unterscheiden sich dort teils von den hier im Dokument verwendeten.↩︎
Es ist erneut zu beachten, dass dort die Bezeichnung Aspekt in einer anderen Bedeutung als hier im Dokument verwendet wird, siehe dazu eine Diskussion bei Etzold (2021, 72 f.).↩︎
Für eine geometrische Interpretation dieser Formel siehe auch Wikipedia (2021a, Abschn. 2). Hat man diese Interpretation im Hinterkopf, muss man sich nicht einmal die Formel merken.↩︎
Zur Diskussion der Vorstellung, was eine Tangente ist, siehe auch Greefrath et al. (2016, S. 149)↩︎