8 Aufgabengestaltung
Ziele
- Sie kennen Möglichkeiten, Aufgaben je nach ihrer Funktion und den auszubildenden Fähigkeitsaspekten auszuwählen bzw. zu erstellen.
- Sie können Aufgaben aus Schulbüchern für enstpechende Funktionen und Fähigkeitsaspekte anpassen.
- Sie kennen Differenzierungsmöglichkeiten mithilfe von Aufgaben, insbesondere durch geeignete Hilfestellungen.
Material
In der Veranstaltung Einführung in die Mathematikdidaktik lern(t)en Sie zentrale Aufgabentypen kennen, die Ihnen Aussage über die Offenheit von Aufgaben liefern (siehe auch Bruder, o. J., S. 2). Weiterhin wird an dieser Stelle davon ausgegangen, dass Sie Operatoren kennen, die für eine präzise Formulierung von Aufgabenstellungen genutzt werden können (siehe auch Institut für Qualitätsentwicklung im Bildungswesen, 2019; Ministerium für Bildung, Jugend und Sport des Landes Brandenburg, 2015a, S. 11). Dieses Kapitel soll Ihnen darauf aufbauend eine Sammlung unterrichtspraktischer Maßnahmen anbieten, Aufgaben zu gestalten. Explizite Bezüge zu tätigkeitstheoretischen Grundlagen finden Sie am Ende des Kapitels in Abschnitt 8.4.
8.1 Funktionen von Aufgaben
»Eine Aufforderung zum Lern-Handeln im Mathematikunterricht wird als Aufgabe bezeichnet« (Bruder, 2012, S. 19, Hervorhebung im Original). Mit diesem Aufgabenbegriff sind Sie nun als Lehrkraft gefordert, Ihre Schülerinnen und Schüler anzuregen, sich aktiv mit mathematischen Lerngegenständen auseinanderzusetzen. Dabei sollten Sie sich der verschiedenen möglichen Funktionen von Aufgaben bewusst sein, da dies jeweils die Art und Weise, wie Sie Aufgaben formulieren und sie im Unterricht einsetzen, beeinflussen (vgl. Leuders, 2015, S. 439; SINUS Bayern, o. J.). Die hier angebrachten Beispiele beziehen sich auf den Lerngegenstand Prozentrechnung.
Aufgaben können dem Erkunden, Entdecken und Erfinden dienen. Diese in der Regel am Anfang eines Themengebiets stehenden Aufgaben sollten möglich offen formuliert sein und in besonderer Weise Motivation schaffen, sich mit dem Lerngegenstand erstmals auseinanderzusetzen (siehe Abbildung 8.1). An dieser Stelle können auch typische W-Fragen gestellt werden – es ist im Sinne der Offenheit nicht zwingend notwendig, sich an den Operatoren zu orientieren.

Abb. 8.1: Erkundungsaufgabe zur Prozentrechnung (Leuders et al., 2015, S. 223)
Aufgaben zum Sammeln, Sichern und Systematisieren greifen vorherige Ideen auf, mit denen dann eine gewünschte mathematische Struktur herausgearbeitet werden soll (siehe Abbildung 8.2). In derartigen Aufgaben können Schülerinnen und Schüler auch angeleitet werden, sinnvolle Repräsentationen zu nutzen, um Grundvorstellungen auszubilden.

Abb. 8.2: Systematisierungsaufgabe zur Prozentrechnung (Leuders et al., 2015, S. 226)
Üben, Festigen und Wiederholen sind weitere wesentliche Funktionen von Aufgaben im Mathematikunterricht. Hier sollten Sie eine möglichst große Vielfalt an Fähigkeitsaspekten ansprechen (siehe Abschnitt 8.2.1), um sowohl Automatisierungsprozesse als auch den Transfer anzuregen. Sowohl geschlossene als auch teilweise geöffnete Aufgaben bieten sich hier an – auch sind die verschiedenen Anforderungsbereiche anzusprechen, was sich in einer gezielten Auswahl an Operatoren widerspiegeln sollte (siehe Abbildung 8.3).

Abb. 8.3: Übungsaufgaben zur Prozentrechnung (Leuders et al., 2015, S. 232)
Das Vertiefen, Strukturieren und Vernetzen stärkt das Kompetenzerleben der Schülerinnen und Schüler. Die Aufgaben werden wieder offener und können mit anderen Lerngegenständen in Bezug gebracht werden. Auch können Sonder- oder Grenzfälle der bisher betrachteten Aufgaben nun verstärkt eine Rolle spielen (siehe Abbildung 8.4).

Abb. 8.4: Vertiefungsaufgabe zur Prozentrechnung (Leuders et al., 2015, S. 241)
Die bisher genannten Funktionen hängen oftmals eng mit entsprechenden Unterrichtsphasen zusammen. Davon unabhängig können Aufgaben auch die Funktion des Differenzierens haben. Maßnahmen dafür werden in Abschnitt 8.3 näher erläutert.
Weiterhin ist zwischen Lernaufgaben und Leistungsaufgaben zu unterscheiden. Letztere spielen bei der Selbsteinschätzung, Diagnose und Leistungsmessung eine besondere Rolle (siehe Abbildung 8.5). Insbesondere für solche Aufgaben sollten Operatoren genutzt werden, um die gewünschten Komptenzen gezielt überprüfen zu können, Erwartungen an die Schülerinnen und Schüler transparent zu machen und eine Vergleichbarkeit zu sichern.

Abb. 8.5: Selbsteinschätzungsaufgabe zur Prozentrechnung (Leuders et al., 2015, S. 244)
8.2 Produktives Üben
8.2.1 Fähigkeitsaspekte
Nicht selten wird man in Schulbüchern mit sogenannten Aufgabenplantagen konfrontiert, also einer Vielzahl an Aufgaben immer derselben Art. Diese haben in der Regel das (berechtigte) Ziel, dass bestimmte Rechenoperation durch wiederholtes Üben automatisiert durchgeführt werden können. Im Schulalltag besteht jedoch die Gefahr, dass das Üben im Mathematikunterricht dann zum alleinigen Päckchenrechnen verkommt, was der Vielzahl an Fähigkeitsaspekten, die ausgeprägt werden sollen, nicht gerecht wird.
Diese Fähigkeitsaspekte sind nach Leuders (2009, S. 133):
- Kenntnisse, es kann z. B. die Definition eines math. Inhalts mit eigenen Worten wiedergegeben werden.
- Fertigkeiten, es können z. B. bestimmte Rechenoperationen durchgeführt werden.
- Verstehen/Vorstellungen, es kann z. B. an einem Bild der entsprechende math. Inhalt erklärt werden.
- Anwendungsfähigkeit, es können z. B. unbekannte Situationen mithilfe des math. Inhalts gelöst werden.
- (übergreifende) Strategien, es können z. B. Heurismen (vgl. Kuzle, o. J.) mithilfe des math. Inhalts angewandt werden.
- Reflexionsfähigkeit, es kann z. B. beurteilt werden, inwieweit der math. Inhalt in einer Situation relevant ist.
- Einstellungen, es besteht z. B. die Bereitschaft, sich mit dem math. Inhalt auseinanderzusetzen.
Diese Fähigkeitsaspekte sind nicht als Stufen aufzufassen, sondern gleichermaßen und unabhängig voneinander bedeutsam (Leuders, 2009, S. 133).
8.2.2 Aufgaben verändern
Einerseits sollten Sie als Lehrkraft in der Lage sein, zielgerichtet je nach Fähigkeitsaspekt Aufgaben auszuwählen. Andererseits, und das ist dann notwendig, wenn Sie keine guten Aufgaben finden, müssten Sie auch selbst welche entwickeln können – was jedoch sehr zeitaufwendig ist. Ein in der Unterrichtspraxis effektiver Umgang ist das Verändern von existierenden Aufgaben, um diese produktiver zu machen, d. h. vielfältige Fähigkeitsaspekte anzusprechen.
Leuders (2009, 137 ff.) stellt in einer ausführlichen Tabelle (am Beispiel des arithmetischen Mittels) dar, wie man sich ausgehend vom gewünschten Fähigkeitsaspekt (z. B. »Strukturen reflektieren«) und damit zusammenhängenden Aufgabentypen (z. B. »Muster erkennen und erzeugen«) an geeigneten Fragetypen (z. B.»Muster fortsetzen«) orientieren kann, um einen produktiven Umgang mit Aufgaben zu ermöglichen. Mit diesem Hintergrundwissen können Sie Ihren Blick auf existierende Schulbuchaufgaben richten und diese dann zielgerichtet anpassen.
Die soll am Beispiel einer Schulbuchseite zur Prozentrechnung dargestellt werden, siehe Abbildung 8.6.

Abb. 8.6: Schulbuchseite zur Prozentrechnung (Kleine & Ludwig, 2011, S. 65)
Bei Aufgabe 2 könnte ergänzt werden:
Welche Brüche lassen sich besonders leicht, welche schwerer in Dezimalbrüche und Prozent umrechnen? Woran liegt das?
Damit soll die Reflexion darüber angeregt werden, dass das Erweitern und Kürzen, sodass der Nenner 100 ergibt, je nach gegebenem Nenner unterschiedlich schwer sein kann. Hinsichtlich der Tabelle von Leuders (2009, S. 138) kann diese Aufgabe der Situation »Strukturen reflektieren« → »Strukturieren« → »Bewerten« zugeordnet werden. Statt alle Päckchen rechnen zu müssen, könnte nach der obigen Reflexion auch aufgefodert werden:
Wähle eine leichte und eine schwere Teilaufgabe aus und löse sie.
Aufgabe 4 ließe sich ergänzen durch:
Wie ändert sich Lisas Leistung, wenn du weitere Schüsse aufs Tor zielst, die sie alle hält?
Diese Aufgabe betont den Zusammenhang zwischen Grundwert, Prozentwert und Protenzsatz, da jeder weitere Schuss sowohl den Grundwert als auch Prozentwert um 1 erhöht, womit zwar der Prozentsatz zunimmt, aber nicht linear steigt. Damit kann gleichzeitig eine tiefere Beschäftigung mit der dahinterliegenden arithmetischen Struktur angeregt werden. Nach Leuders (2009, S. 137) gehört diese Aufgabe zum Bereich »Probleme lösen« → »Operatives Durcharbeiten« → »Funktionale Abhängigkeit«.
Aufgabe 5 könnte ergänzt werden:
Erfinde eine andere Situation, in der auf dieselbe Art und Weise gerechnet werden kann. Welche deiner Größen entsprechen den »Punkten« und der »Anzahl der Lose« und welche Rolle spielen diese Größen bei der Berechnung?
Hierüber wird eine strukturgleiche Übertragung der gegebenen Situation auf eine neue Situation gefordert. Dies führt dazu, sich tiefer mit dem Zusammenhang aus Rechenoperation und Anwendungskontext auseinanderzusetzen und entspricht bei Leuders (2009, S. 139) der Kategorie »Anwendungen erkunden« → »Anwenden« → »Anwendungen erfinden«.
8.3 Differenzieren
Um differenzierenden Unterricht zu ermöglichen, können Aufgaben entsprechend gestaltet werden. Dies kann mit leichten und schweren Aufgaben erfolgen – es gibt aber noch weitaus mehr Möglichkeiten. Davon sollen hier einige exemplarisch vorgestellt werden, genauere Maßnahmen finden sich in den jeweils zitierten Quellen.
8.3.1 Gestufte Hilfen
Bei komplexen Aufgaben bietet es sich an, den Schülerinnen und Schülern gestufte Hilfen bereitzustellen, damit diese im Lösungsweg individuell unterstützt werden können (siehe auch Zech, 1998, 315 ff.). Auch wenn Motivationshilfen (Die Aufgabe ist nicht so schwer.), Rückmeldungshilfen (Du bist auf einem guten Weg.) oder allgemeine strategische Hilfen (Lies die Aufgabe noch mal durch.) deratige Unterstützungen sind, sollte bei der stoffdidaktisch-orientierten Unterrichtsplanung der Schwerpunkt auf inhaltsorientierten strategischen Hilfen sowie auf inhaltlichen Hilfen im Zusammenhang mit dem Lerngegenstand liegen.
Inhaltsorientierte strategische Hilfen beziehen sich auf typische am Lerngegenstand orientierte Herangehensweisen zur Lösung einer Aufgabe. Mögliche Beispiele sind:
Veranschauliche dir die Situation mit einer Skizze. Stelle eine Gleichung auf. Orientiere dich beim Vorgehen an dem Beispiel, das du bereits gerechnet hast.
Inhaltliche Hilfen beziehen sich direkt auf die mit der Aufgabe verbundenen Begriffe, Regeln und Zusammenhänge. Dies können z. B. sein:
Überlege, was mit dem Flächeninhalt passiert, wenn du die Seitenlängen verdoppelst. Du kannst hier das Kommutativgesetz anwenden.
Zech (1998, S. 315) betont, »nie mehr [zu] helfen als erforderlich«, um eine Aufgabe erfolgreich lösen zu können. Gestufte Hilfen haben demnach die Funktion, trotz ggf. vorhandener Schwierigkeiten Erfolgserlebnisse bei den Schülerinnen und Schülern zu ermöglichen.
8.3.2 Differenzierende Aufgaben
8.3.2.1 Schwierigkeitsbestimmende Merkmale
Ob eine Aufgabe leicht oder schwer ist, wird natürlich stets subjektiv beeinflusst. Dennoch können schwierigkeitsbestimmende Merkmale von Aufgaben identifiziert werden, die bspw. bei der Konstruktion differenzierender Aufgaben hilfreich sind. Nach Drüke-Noe (2018, S. 11) sind diese Merkmale:
- Zugehörigkeit zu einer curricularen Wissensstufe,
- Komplexität und Qualität einer erforderlichen Modellierung,
- Offenheit des Modellierungsprozesses,
- Art des Kontextes,
- Erfordernis, mathematische Argumente zu formulieren,
- Anzahl zu steuernder Denkprozesse,
- Technische Komplexität,
- „Umfang“ eines Verarbeitungsprozesses (u. a. Anzahl der Rechenschritte, Art des Zahlenmaterials),
- Sprachlogische Komplexität.
Abbildung 8.7 zeigt eine mögliche Realisierung zur Generierung unterschiedlich schwerer Aufgaben.

Abb. 8.7: Unterschiedlich schwere Aufgaben zum Prismenvolumen (aus Drüke-Noe, 2018, S. 10)
In der Unterrichtspraxis kann dies nun bedeuten, dass Sie auswählen, welche Schülerinnen und Schüler welche Aufgaben lösen (sogenannte paralleldifferenzierende Aufgaben, vgl. Leuders, 2015, S. 441), Sie können die Auswahl den Lernenden selbst überlassen oder auch eine Stufung im Schwierigkeitsgrad vornehmen, die dann durchlaufen werden soll (gestuft differenzierende Aufgaben).
8.3.2.2 Blütenaufgaben
Eine besondere Form gestufter Aufgaben sind Blütenaufgaben. Diese sind dadurch gekennzeichnet, dass der Offenheitscharakter der Teilaufgaben steigt, wobei alle Teilaufgaben einem gemeinsamen Kontext zuzuordnen sind. Die Schülerinnen und Schüler entscheiden dabei selbst, wie weit sie in der Bearbeitung der Aufgabe vordringen, womit Blütenaufgaben anforderungsgestuft und selbstdifferenzierend sind (vgl. Bruder et al., 2015, 528 f.).
Einen etwas ausführlicheren Hintergrund und einige Beispiele zeigt ein Video von Quarder (2020).
8.3.3 Natürliche Differenzierung
Eine noch offenere und für die Unterrichtsplanung durchaus anspruchsvollere Form ist die natürliche Differenzierung. Nach Krauthausen & Scherer (2010, S. 5 f.) weist eine natürlich differenzierte Lernumgebung folgende Merkmale auf:
Alle Schülerinnen und Schüler arbeiten an einem gemeinsamen Lerngegenstand mit demselben Lernangebot, d. h. allen wird dasselbe Material zur Verfügung gestellt.
Das Material weist eine inhaltliche Ganzheitlichkeit auf, d. h. es ist komplex genug, um sich tiefgründig mit dem Lerngegenstand auseinandersetzen zu können.
Es erfolgt (durch die Lehrkraft) eine fachliche Rahmung, die naturgemäß zu Fragestellungen unterschiedlichen Schwierigkeitsgrades führt. Daraufhin haben die Schülerinnen und Schüler die Wahl, auf welchem Nivau die Problemstellung betrachtet wird – das Material muss hier also verschiedene Niveaus gleichermaßen ermöglichen.
Den Schülerinnen und Schülern ist es freigestellt, welche Wege, Hilfsmittel und Darstellungsweisen genutzt werden, um die Problemstellung zu bearbeiten. Die Lehrkraft hat hier die Veranwortung, die Schülerinnen und Schüler zu befähigen, eine sinnvolle Auswahl zu treffen. Dies kann bspw. durch geeignete Impulse erfolgen, auch ist ggf. eine explizite Heurismenschulung notwendig.
Letztlich ist natürliche Differenzierung durch ein intensives soziales Mit- und Voneinanderlernen geprägt, wofür eine kommunikationsfreundliche Umgebung geschaffen werden muss. Dies betrifft z. B. die Diskussion unterschiedlicher Lösungswege, natürlich entstandene (ggf. abweichende) Fragestellungen oder auch unterschiedliche Auffassungen.
Bisher existieren wenige Aufgaben zur natürlichen Differenzierung für die Sekundarstufe. Ein Beispiel zur Bruchrechnung zeigen Föckler et al. (2018, S. 2).
8.4 Theoretischer Rückblick
Wirft man einen tätigkeitstheoretischen Blick auf Aufgaben im Mathematikunterricht, kann man diese als Aufforderung verstehen, Lernhandlungen durchzuführen (siehe Beginn des Abschnitts 8.1). Entsprechend der im Kapitel 6 dargestellten Überlegungen, bedarf es vor einer Ausführung des Aufgabenlösen einer Zielbildung sowie einer Orientierungsgrundlage.
Die Zielbildung erfolgt in diesem Fall über die selbst gestellte Lernaufgabe (vgl. Bruder, 2023), die man auch als interne Aufgabe20 bezeichnen kann. Damit soll ausgedrückt werden, dass die (von außen) gestellte Aufgabe zunächst von den Schülerinnen und Schülern verarbeitet und mit einer individuellen Zielbildung (als ideell vorweggenommenes Ergebnis der noch durchzuführenden Handlung) in Bezug gebracht wird. Zu beachten ist hierbei, dass die interne Aufgabe »nicht notwendigerweise bezüglich Umfang und Inhalt mit den Erwartungen der Lehrkraft übereinstimmen muss«. Ursachen können hier in fehlenden Kenntnissen, Fähigkeiten und Fertigkeiten liegen, aber auch affektive, motivationale und volitive Gründe können dies beeinflussen (Bruder, 2023).
Hat sich die Schülerin oder Schüler eine interne Aufgabe gestellt, bildet sich (ebenfalls noch vor dem Bearbeiten der Aufgabe) eine Orientierungsgrundlage heraus (vgl. Abschnitt 6.3.2), je nach Qualität als Probierorientierung, Musterorientierung oder Feldorientierung. Diese »ist Voraussetzung für die Bewältigung von aufgabenbasierten Anforderungen, aber zugleich auch ein Ziel individueller Aneignungsprozesse« (Bruder, 2023). Um hochwertige Orientierungsgrundlagen zu ermöglichen und auszubilden, bedarf es also entsprechender Aufgabenstellungen, die nicht ausschließlich eine Probier- oder Musterorientierung forcieren. Eine Maßnahme hierzu ist die Variation der Aufgabentypen und das Öffnen von Aufgaben.
- Wird etwa zur Abbildung 8.8 die Aufgabe »Bestimme den Flächeninhalt des Dreiecks« formuliert, spricht dies v. a. eine Musterorientierung an, da der Aufgabentyp in dieser Form bereits mehrfach geübt wurde.
- Die Aufgabe »Zeichne ein Dreieck mit einem Flächeninhalt von 13 cm².« ermöglicht dagegen alle Orientierungstypen. Die Aufgabe ist sowohl über Versuch und Irrtum lösbar (z. B. mit einem Dynamischen Geometriesystem, das den Flächeninhalt eines Dreicks unmittelbar angeben kann, sobald es gezeichnet ist), als auch mit einer Musterorientierung (wenn man sich an ähnlich durchgeführten Beispielen orientiert) sowie einer Feldorientierung (wenn man sich über den Bezug zur Flächeninhaltsformel darüber im Klaren wird, dass ausschließlich die Grundseite und Höhe des Dreiecks relevant sind – also bspw. auch eine ganze Klasse von Lösungen erzeugt werden kann).
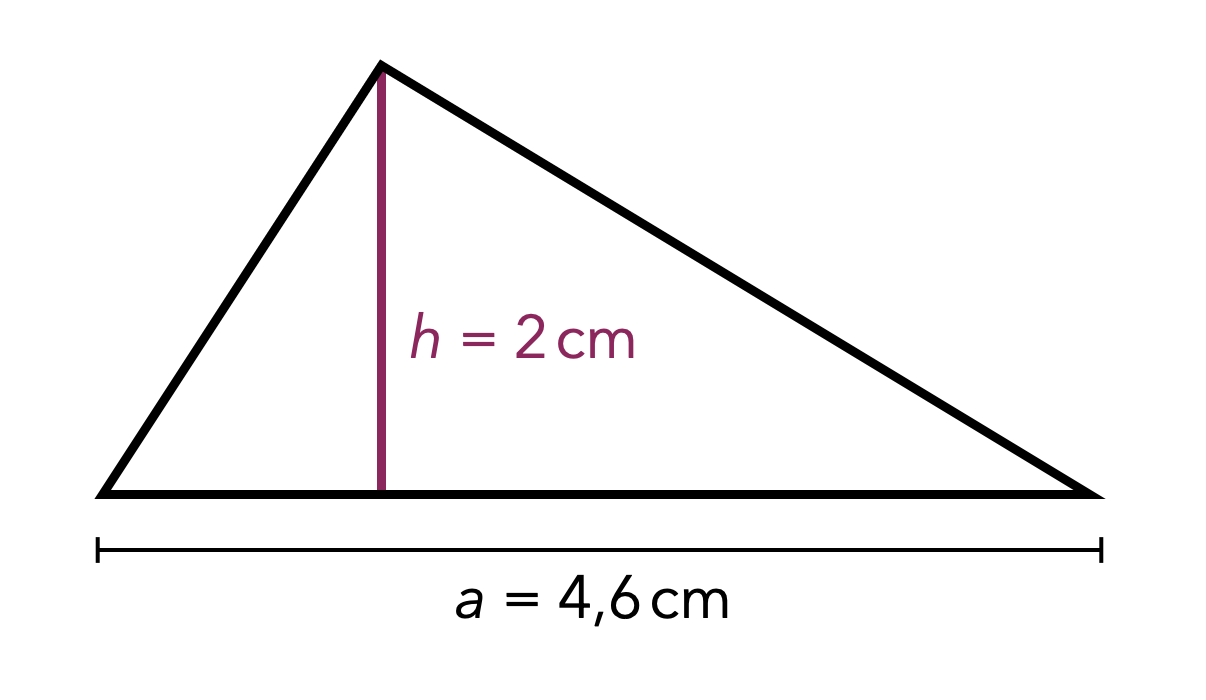
Abb. 8.8: Flächeninhaltsbestimmung mit Musterorientierung
Die Ermöglichung vielfältiger Orientierungsgrundlagen trägt damit auch zur Differenzierung des Unterrichts bei.
References
Bruder verwendete diese Bezeichnung am 2. September 2022 im Rahmen eines Konferenzvortrags auf der Jahrestagung der Gesellschaft für Didaktik der Mathematik in Frankfurt am Main.↩︎