14 Leitidee Daten und Zufall
Material
Literaturempfehlungen
14.1 Strukturierung der Leitidee
| Dokument | Bezeichnung der Leitidee |
|---|---|
| Bildungsstandards Primarbereich (2005) | Daten, Häufigkeit und Wahrscheinlichkeit |
| Bildungsstandards Primarbereich (2022) | Daten und Zufall |
| Bildungsstandards Mittlerer Schulabschluss (2004) | Daten und Zufall |
| Bildungsstandards Erster und Mittlerer Schulabschluss (2022) | Daten und Zufall |
| Rahmenlehrplan Brandenburg, Jahrgangsstufen 1 – 10 | Daten und Zufall |
| Bildungsstandards Allgemeine Hochschulreife (2012) | Daten und Zufall |
| Rahmenlehrplan Brandenburg, Gymnasiale Oberstufe | Daten und Zufall |
Auch für diese Leitidee hat das LISUM (o. J.-b) für die Jahrgangsstufen 1 – 10 ein Konzeptbild herausgegeben (siehe Abbildung 14.1), ergänzt durch einen didaktischen Kommentar von Kortenkamp & Kuzle (o. J.-a) und Materialien zur Diagnose und Förderung (LISUM, o. J.-a).
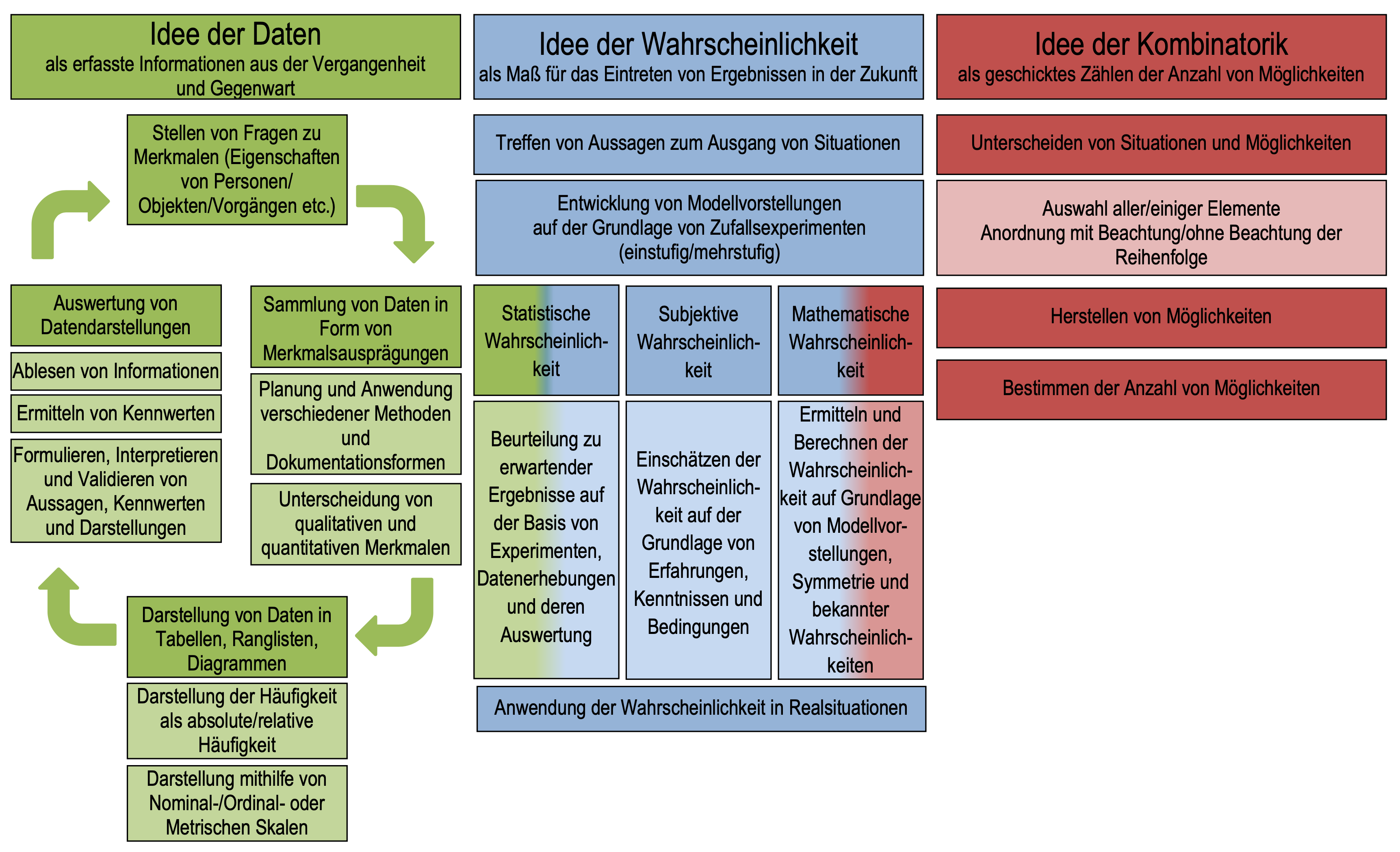
Abb. 14.1: Konzeptbild zur Leitidee Daten und Zufall (LISUM, o. J.-b)
Aus den Beschreibungen in den Bildungsstandards für die Sekundarstufen (Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, 2012, 21; 2022a, 22 f.) lassen sich folgende bedeutsamen Lerngegenstände folgern:
Bedeutsame Lerngegenstände
- statistische Erhebungen und deren Darstellungen
- Simulationen
- statistische Kenngrößen (z. B. Minimum, Maximum, arithmetisches Mittel, Median, Spannweite, Quartile),
- Diagramme (z. B. Säulen- oder Balkendiagramm, Histogramme, Kreisdiagramm, Liniendiagramm, Boxplot)
- Zufallserscheinungen und Wahrscheinlichkeitsaussagen
- Zufallsexperimente, relativen Häufigkeiten und Wahrscheinlichkeiten
- ein- oder mehrstufige Zufallsexperimente
- bedingte Wahrscheinlichkeiten
- Baumdiagramme und Vierfeldertafeln
- stochastische Unabhängigkeit
- diskrete und stetige Zufallsgrößen
- Binomialverteilung
- Normalverteilung
- Hypothesentests
Im Folgenden sollen einige Grundgedanken zur Stochastik, insbesondere im Zusammenhang mit dem Begriff des stochastischen Vorgangs, diskutiert werden. Anschließend erfolgen noch Darstellungen zum Umgang mit bedingten Wahrscheinlichkeiten.
14.2 Stochastische Vorgänge
14.2.1 »Zufallsexperiment«-Kritik
Krüger et al. (2015, 219 f.) argumentieren, dass der häufig verbreitete Begriff des Zufallsexperiments aus fachlicher wie didaktischer Sicht ungeeignet für den Unterricht erscheint. Sie begründen dies u. a. mit der Nichtnotwendigkeit des Begriffs in der Fachmathematik und damit, dass es sich nicht um ein Experiment im naturwissenschaftlichen Sinne der Hypothesenüberprüfung unter kontrollierten Bedingungen handele – die oftmals formulierte Regel der »beliebige[n] Wiederholbarkeit unter gleichen Bedingungen« sei letztlich schon ein Modell mit der Annahme der stochastischen Unabhängigkeit (Krüger et al., 2015, S. 219). Spiele, in denen der Zufall eine Rolle spielt, sind für den Mathematikunterricht höchst relevant – sollten aber nicht als Experimente aufgefasst werden. Stattdessen werden für die Grundschule der Begriff Vorgang mit mehreren möglichen Ergebnissen und für die weiterführenden Schulen der Begriff stochastischer Vorgang vorgeschlagen (Krüger et al., 2015, S. 220)
Für die tatsächliche Unterrichtsausführung ist dies insofern problematisch, da der Begriff Zufallsexperiment i. d. R. Bestandtteil der Lehrpläne ist (siehe z. B. Ministerium für Bildung, Jugend und Sport des Landes Brandenburg, 2015b, 59, 61) und damit unterrichtet werden muss. Sie als Lehrkraft sollten also stets die an der Verwendung des Begriffs vorgebrachte Kritik im Hinterkopf haben und dies sensibel bei Ihrer Unterrichtsgestaltung beachten. Dies kann etwa bedeuten, dass Sie dennoch eine übliche Definition des Begriffs Zufallsexperiment nutzen (siehe Abbildung 14.2), aber im Unterricht die Unterschiede zu echten Experimenten thematisieren und über geeignete Beispiele und Gegenbeispiele den Begriff ausschärfen.

Abb. 14.2: Schulbuchdefinition des Begriffs Zufallsexperiment (Adam & Kleine, 2016, S. 18)
14.2.2 Modellierungsstruktur
Grundsätzlich ist es Aufgabe der Stochastik, reale Prozesse zu modellieren, um diese mit mathematischen Mitteln, also einem theoretischen Modell, greifbar (und bearbeitbar) zu machen. Dazu ist es normalerweise notwendig, die reale Situation erst einmal zu vereinfachen und in ein Realmodell zu überführen (siehe Abbildung 14.3). Dieses Vorgehen ist nicht spezifisch für die Stochastik – jedoch ist der Zwischenschritt des Realmodells hier aufgrund der vielfältigen Modellierungsmöglichkeiten von besonderer Bedeutung. Der Begriff stochastischer Vorgang ist dann »auf der Ebene der Realmodelle angesiedelt«, mit der Verwendung des Begriffs Zufallsexperiment dagegen »verwischt man die Grenzen zwischen Realität und Modellebene« (Krüger et al., 2015, 219 f.).
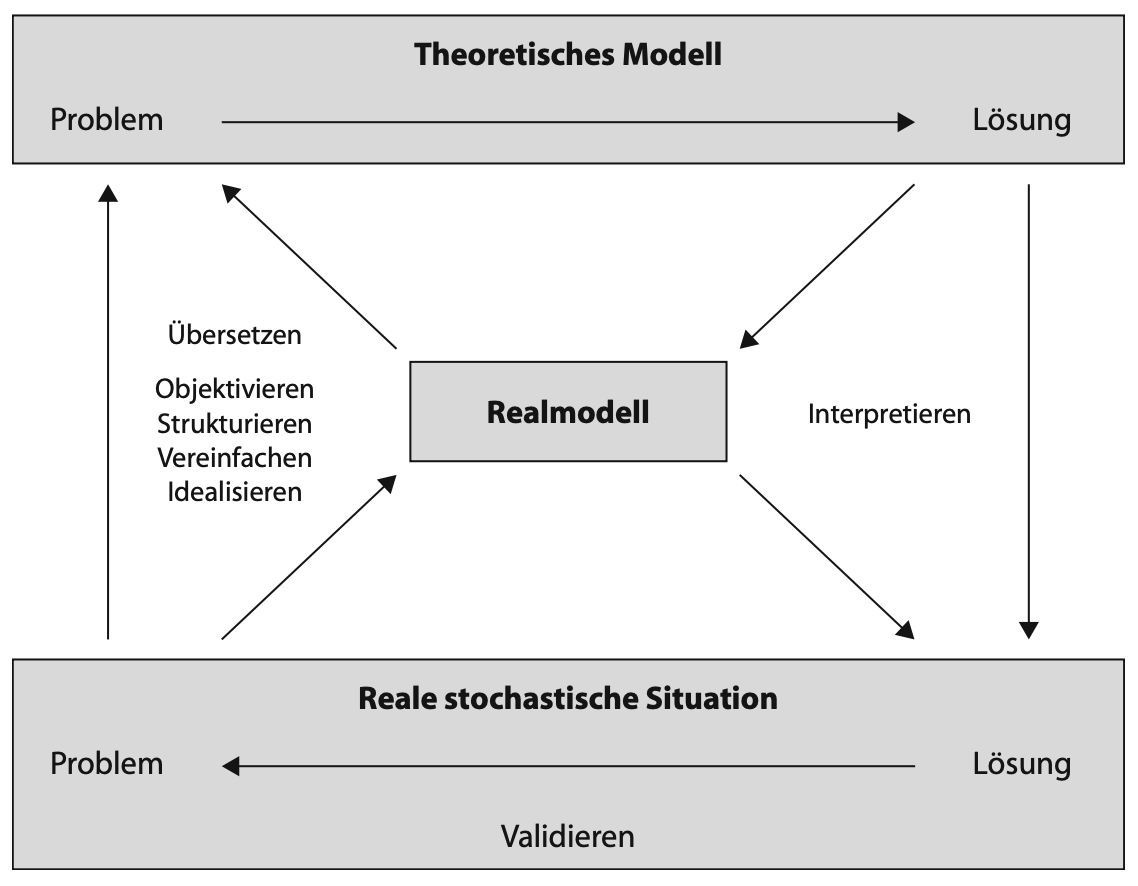
Abb. 14.3: Modellierungsstruktur in der Stochastik (Krüger et al., 2015, S. 13)
Aufbauend auf diese Struktur (die »nicht als expliziter Gegenstand des Stochastikunterrichts aufzufassen« ist, Krüger et al., 2015, S. 13) können Sie Ihre Diskussionen im Unterricht leiten und Schwierigkeiten der Schülerinnen und Schüler besser einordnen, z. B.:
Wenn ein Würfel geworfen wird (reale Situation) und man die Wahrscheinlichkeit für eine Augenzahl angibt (theoretisches Modell), geht man davon aus, dass der Würfel aus sechs identischen Seiten besteht und in sich homogen ist (Realmodell). Mögliche Fragen, die auf eine solche Denkweise hinarbeiten, könnten sein: Welche Annahmen triffst du? Welche Eigenschaften muss der Würfel haben, damit du so rechnen darfst?
Wenn erstmals Zufallsgeräte (übrigens auch ein Begriff auf der Ebene der Realmodelle) genutzt werden, muss eine Untergeneralisierung vermieden werden, es sollten also frühzeitig auch nicht-Laplace-Geräte eingesetzt werden, wie Reißzwecken, Quader, sogenannte Riemer-Würfel (Riemer, 1988) oder auch Würfel-Schweine (Wikipedia, o. J.).
Wenn eine Schülerin oder ein Schüler nicht in der Lage ist, für das Ziehen einer Herz-Karte aus einem Skatblatt die Wahrscheinlichkeit anzugeben, sollten Sie als Lehrkraft herausfinden, auf welcher Ebene Schwierigkeiten bestehen. Wird die reale Situation nicht verstanden (weil z. B. die Spielkartenfarben oder der Begriff Skatblatt unbekannt sind)? Bestehen Schwierigkeiten im Aufstellen eines Realmodells (dass also das Ziehen jeder Karte mit derselben Wahrscheinlichkeit verbunden ist und dafür die Anzahl der relevanten Karten bestimmt werden muss)? Oder sind Defizite in der Theorie verortet (weil etwa nicht die Laplace-Formel für die Berechnung der Wahrscheinlichkeit angewandt werden kann oder gar Schwierigkeiten bei der Division bestehen)?
14.2.3 Prozessbetrachtung
Zur Unterstützung der Schülerinnen und Schüler in der Beschreibung stochastischer Vorgänge schlagen Krüger et al. (2015, 14 f.) die Nutzung einer Prozessbetrachtung vor (siehe Abbildung 14.4).
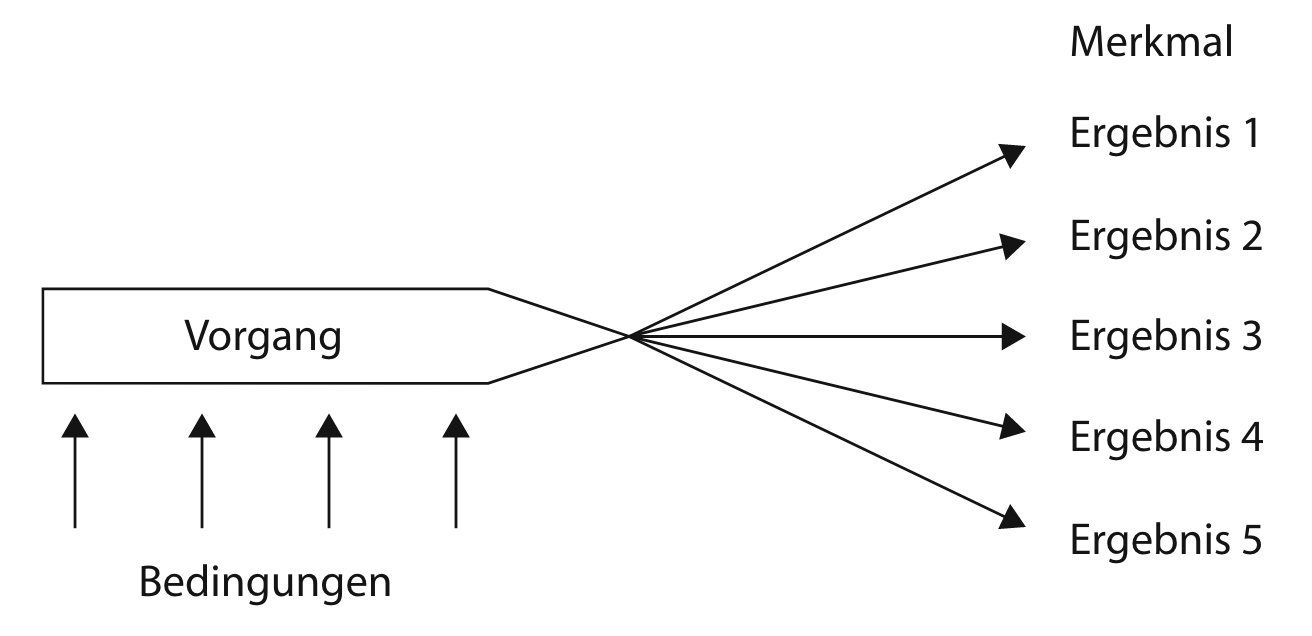
Abb. 14.4: Vorgangsbetrachtung nach Krüger et al. (2015, S. 16)
Es handelt sich hierbei um eine schematische Darstellung, wobei vier wesentliche Fragen relevant sind (Krüger et al., 2015, S. 15):
- »Welcher Vorgang läuft mit welchen Objekten oder Personen ab?«
- »Welches Merkmal interessiert mich? Wie kann ich das Merkmal erfassen?«
- »Welche Ergebnisse sind möglich?«
- »Welche Bedingungen beeinflussen den Vorgang?«
Das Schema kann im tätigkeitstheoretischen Sinne als Lernmodell aufgefasst werden, da es die Struktur des stochastischen Vorgangs darstellt und den Weg zur Struktur sichtbar macht. Ein solches Vorgehen ist dabei sowohl für Fragen der Wahrscheinlichkeitsrechnung als auch für die Beschreibung von Statistiken möglich, womit auch beides als Teildisziplinen der Stochastik sichtbar werden kann. Abbildung 14.5 zeigt exemplarisch zwei derartige Prozessbetrachtungen.
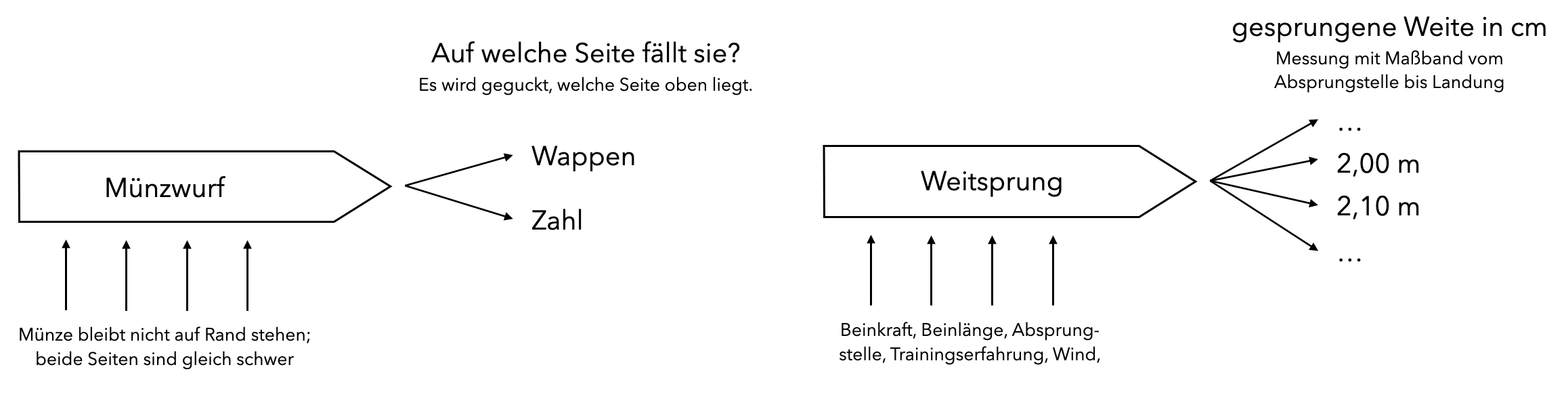
Abb. 14.5: Prozessbetrachtungen für zwei stochastische Vorgänge
14.3 Bedingte Wahrscheinlichkeiten
Bei der Betrachtung von Situationen, in denen bedingte Wahrscheinlichkeiten eine Rolle spielen, haben Schülerinnen und Schüler (und nicht nur die) oftmals die Schwierigkeit, die verschiedenen Bedingungen auseinanderzuhalten, weshalb fehlerhafte Schlüsse gezogen werden (vgl. Binder et al., 2020).
Ist beispielsweise bekannt, dass ein Corona-Test mit 90%-iger Wahrscheinlichkeit eine Person, die an Corona erkrankt ist, auch positiv testet und mit 95%-iger Wahrscheinlichkeit eine Person, die nicht an Corona erkrankt ist, auch negativ testet, so stellt sich die Frage, wie hoch die Wahrscheinlichkeit ist, dass man tatsächlich an Corona erkrankt ist, wenn der Test positiv ausfällt. Um diese Frage zu beantworten, ist es weiterhin noch nötig zu wissen (oder zu schätzen), wie hoch der Anteil tatsöchlich erkrankter Personen in der Gesamtbevölkerung ist. Geht man von einem Anteil von 1% aus, so stellt Abbildung 14.6 eine (nicht maßstäbliche) Vierfeldertafel dieser Situationen dar.
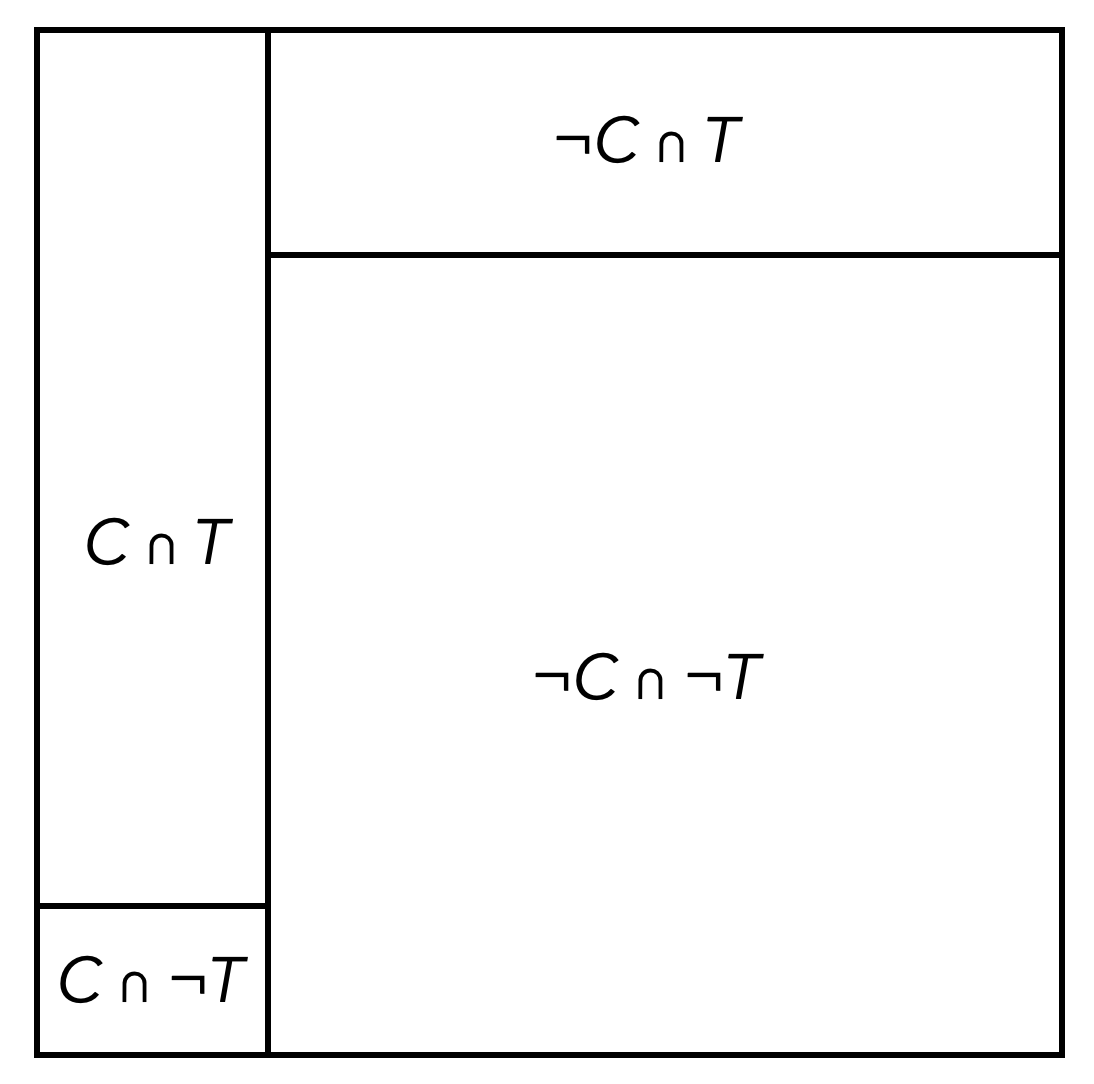
Abb. 14.6: Vierfeldertafel für bedingte Wahrscheinlichkeiten
Es sind demnach bekannt:
\[\begin{align} P(C) &= 0,\!01 \ \mathrm{(Prävalenz)}\\ P_C(T) &= 0,\!95 \ \mathrm{(Sensitivität)}\\ P_{\neg C}(\neg T) &= 0,\!99 \ \mathrm{(Spezifität)} \end{align}\]
Grundsätzlich gilt als Definition für bedingte Wahrscheinlichkeiten: \[P_B(A) = \frac{P(A\cap B)}{P(B)}\]
Nach dem Satz von Bayes und dem Satz von der totalen Wahrscheinlichkeit gilt: \[P_B(A) = \frac{P(A)\cdot P_A(B)}{P(B)} = \frac{P(A)\cdot P_A(B)}{P(A)\cdot P_A(B)+P(\neg A)\cdot P_{\neg A}(B)}\] Hieran zeigt sich schon, dass Schülerinnen und Schüler Schwierigkeiten haben könnten, wenn sie nicht die hinter den Formeln liegenden Vorstellungen entwickeln, welche Wahrscheinlichkeiten jeweils aufeinander Bezug genommen werden. Geeignete Repräsentationen sollen nun helfen, die Zusammenhänge nachvollziehen zu können. Die Vierfeldertafel aus Abbildung 14.6 ist eine solche. Abbildung 14.7 zeigt, wie die Wahrscheinlichkeiten \(P(C)\), \(P_C(T)\) und \(P_T(C)\) darin jeweils als Anteil einer Teilmengenbeziehung aufgefasst werden können.
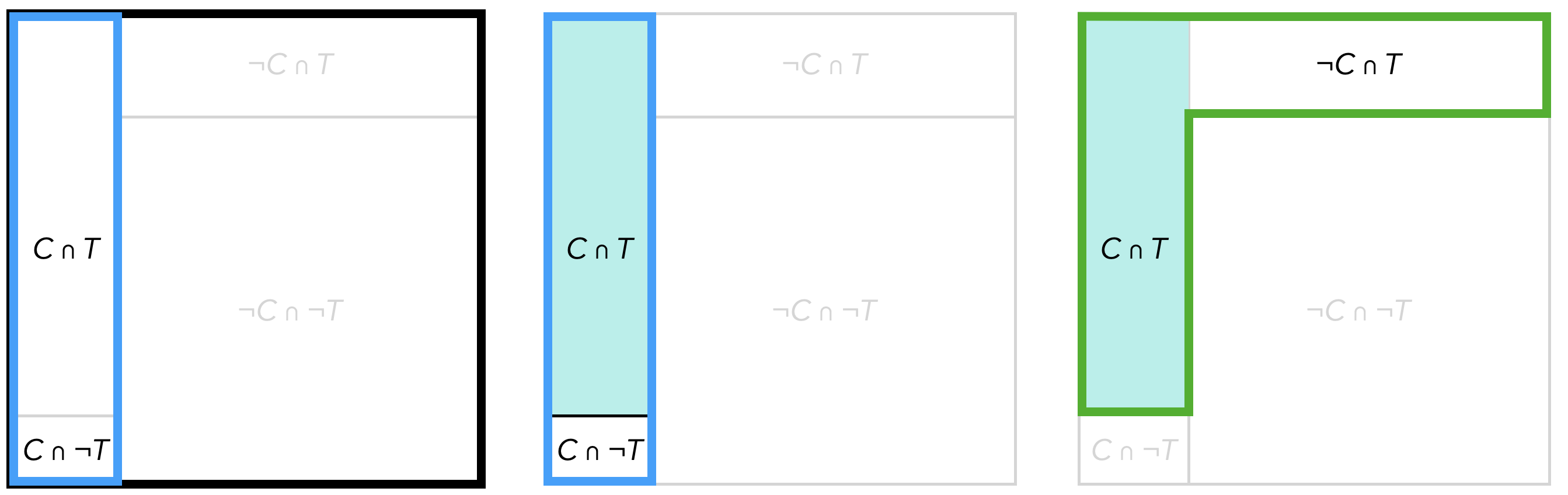
Abb. 14.7: Vierfeldertafeln zur Visualisierung der Wahrscheinlichkeiten \(P(C)\), \(P_C(T)\) und \(P_T(C)\)
Als Repräsentation ebenfalls verbreitet sind sogenannte Doppelbäume, siehe Abbildung 14.8. Auch dort kann nachvollzogen werden, welche Beziehung jeweils betrachtet wird.
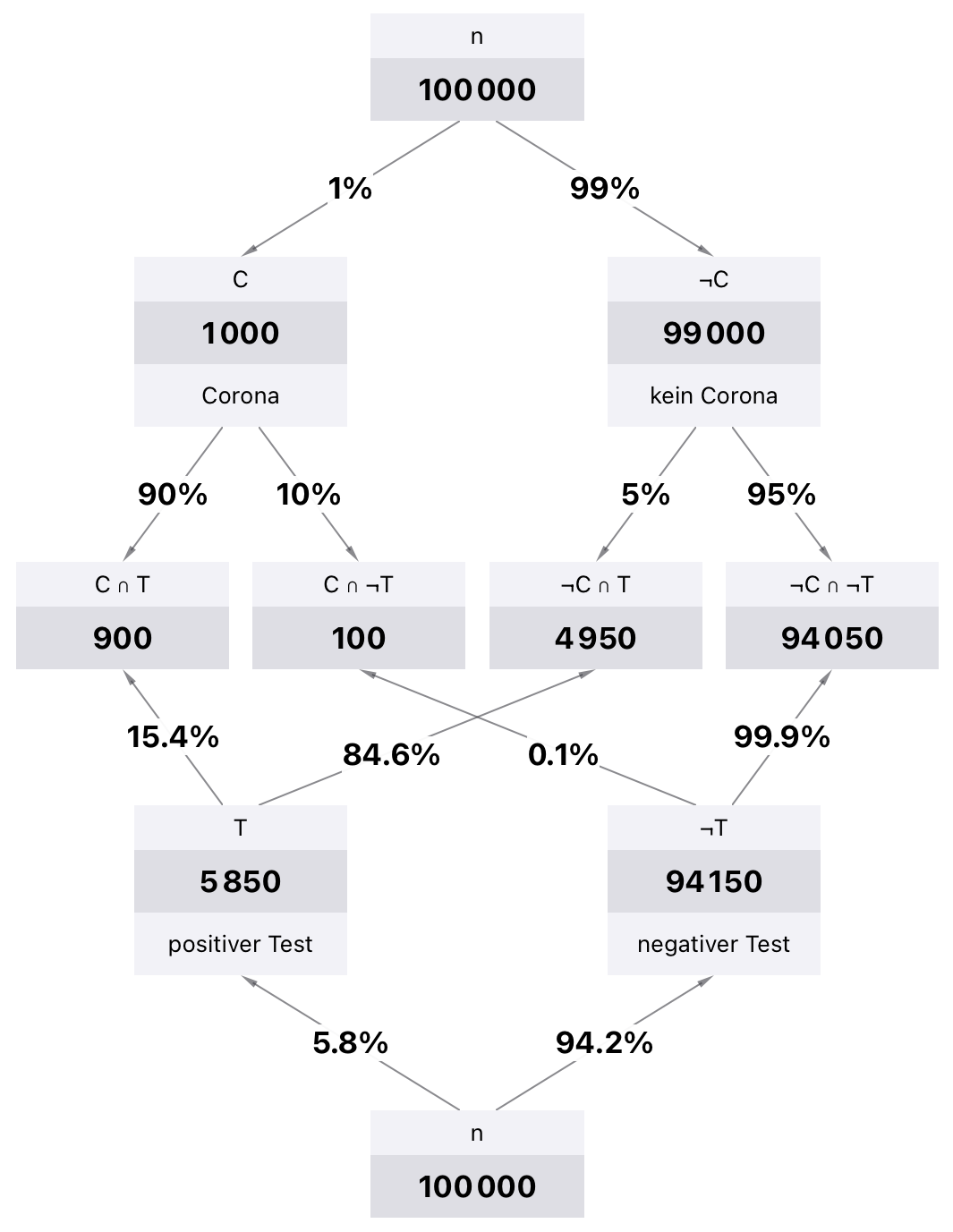
Abb. 14.8: Doppelbaum für bedingte Wahrscheinlichkeiten
Nach Binder et al. (2020) bietet sich ebenfalls ein Häufigkeitsnetz an, siehe Abbildung 14.9. Gegenüber den bisherigen Darstellungen können in diesem auch direkt die Schnittwahrscheinlichkeiten abgelesen werden.
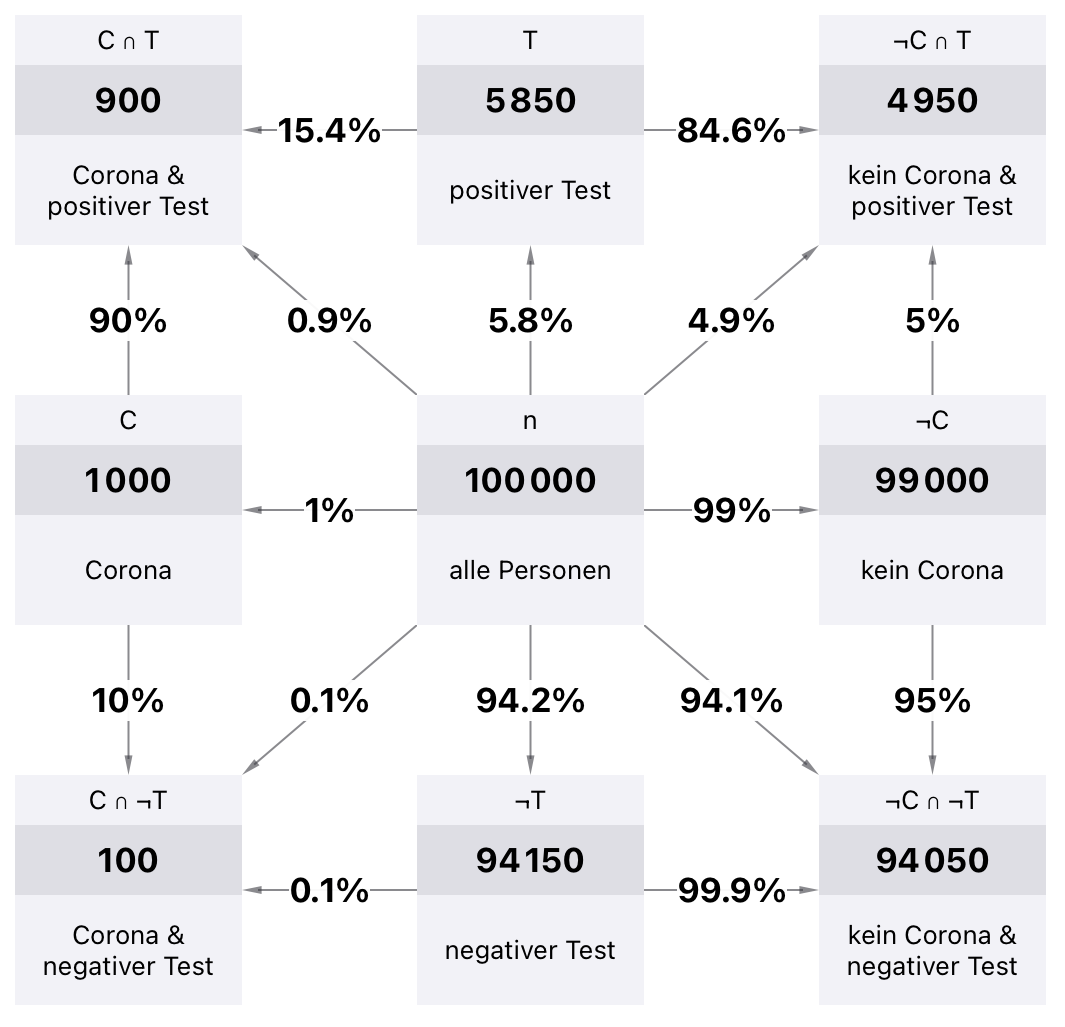
Abb. 14.9: Häufigkeitsnetz für bedingte Wahrscheinlichkeiten
Als weitere Unterstützungsmöglichkeit, so hat es sich auch in empirischen Studien gezeigt (vgl. Binder et al., 2020), bietet es sich an, mit absoluten Häufigkeiten statt Wahrscheinlichkeiten in den Repräsentationen zu arbeiten. Diese bieten Schülerinnen und Schülern eine bessere Zugänglichkeit zur Thematik und über Anteilsbetrachtungen können dann auch die Wahrscheinlichkeiten bestimmt werden.36 Als (fiktive) Anzahl für die Grundgesamtheit bietet sich eine hohe Zehnerpotenz an, da so auch noch kleine Anteile mit sinnvollen (ggf. gerundeten) ganzen Zahlen bestimmt werden können.
References
Mathematisch präzise müsste hier von relativen Häufigkeiten anstatt von Wahrscheinlichkeiten gesprochen werden.↩︎