3 Sinn und Bedeutung

Ziele

• Sie kennen das Konzept der fundamentalen Ideen und greifen auf dieses zurück, wenn sie Sie die Bedeutung einzelner Lerngegenstände für den Mathematikunterricht diskutieren.
• Sie können die Grundvorstellungsidee beschreiben und wissen über deren Bedeutung für den Mathematikunterricht.
• Sie kennen Grundvorstellungen zu einzelnen mathematischen Begriffen.

Material

• Folien zum Kapitel 3 (pdf, Keynote)

3.1 Allgemeine Hinweise

In der Auffassung, dass Lernen als individuelle Aneignung gesellschaftlichen Wissens und Könnens angesehen wird (siehe auch Abschnitt 1.2), erscheint es zweckmäßig, diese Unterscheidung zwischen Individuum und Gesellschaft auch hinsichtlich der Semantik eines Lerngegenstands vorzunehmen.

Im Folgenden wird daher mit der gesellschaftlichen Sicht die Bedeutung eines Lerngegenstands verfolgt. Dabei bietet es sich an, mehrere Perspektiven zu verfolgen. Angelehnt an Feldt-Caesar (2017, 124 f.)⁷ können dies sein:

• fachwissenschaftliche Bedeutung: Hier wird untersucht, inwieweit der jeweilige Lerngegenstand für die Mathematik selbst bedeutsam ist, auch hinsichtlich der Anschlussfähig innerhalb der Fachsystematik. Es bietet sich bei der Diskussion eine Orientierung an fundamentalen Ideen der Mathematik an (siehe Abschnitt 3.2).

• gesellschaftliche Bedeutung: Dabei wurd u. a. die Nützlichkeit und Anwendbarkeit des Lerngegenstands für die Gesellschaft diskutiert, also bspw. welchen Beitrag ein bestimmter Lerngegenstand leistet, gesellschaftliche Probleme zu lösen. Die Mathematik dient hier »als Mittel, um Probleme aus Alltag, Beruf, Berufsausbildung oder Studium zu lösen« (Feldt-Caesar, 2017, S. 125). Daher kann auch die Bedeutung des jeweiligen Lerngegenstands für die Berufs- oder Studienorientierung Bestandteil der Diskussion sein.

• historische und kulturelle Bedeutung: Nicht zuletzt dient Mathematik auch der kulturellen Bildung, weshalb für einzelne Lerngegenstände auch diskutiert werden sollte, welchen Beitrag diese dafür leisten. Hier bietet es sich z. B. an, die historische Entwicklung eines Lerngegenstands nachzuzeichnen, um dessen Bedeutung hervorzuheben.

Dabei ist zu erwähnen, dass Bedeutungen zu Lerngegenständen im permanenten Wandel sind. So kann es bspw. sein, dass die Entwicklung künstlicher Intelligenz dazu führt, dass bestimmte Lerngegenstände an Bedeuteung verlieren (weil sie etwa verstärkt durch derartige Hilfsmittel übernommen werden), andere dagegen an Bedeutung gewinnen (etwa, wenn man verstehen will, wie KI-Systeme funktionieren).

Auf individueller Ebene wird vom Sinn gesprochen, mit dem ein Lerngegenstand bei einzelnen Schülerinnen und Schülern verbunden wird. Eine in der deutschsprachigen Mathematikdidaktik verbreitete Theorie zur Beurteilung der Sinnkonstituierung ist die Orientierung an Grundvorstellungen (siehe Abschnitt 3.3).

3.2 Fundamentale Ideen

3.2.1 Begriffsklärung

Die Entwicklung fundamentaler Ideen beruft sich auf Bruners Annahme, dass »jedes Kind […] auf jeder Entwicklungsstufe jeder Lehrgegenstand in einer intellektuell ehrlichen Form erfolgreich gelehrt werden« kann (vgl. Bruner, 1976, S. 77). Voraussetzung dafür ist, dass die Struktur eines Inhaltsbereichs in einer Art und Weise präsentiert wird, dass sie dem Kind zugänglich wird. Diese hinter den Dingen liegende Struktur hebt sich vom konkreten Inhaltsbereich ab, ist allgemeinerer Natur und kann daher über fundamentale Ideen beschrieben werden.

Ziel der Orientierung des Unterrichtens an fundamentalen Ideen besteht v. a. darin, die (oftmals) isolierten Stoffelemente einzuordnen und in einem größeren Ganzen zu sehen. Im Umkehrschluss heißt dies aber auch, dass die Auswahl des konkreten Stoffes daran orientiert sein muss, wie dieser dazu beitragen kann, den dahinter liegenden mathematischen Kern und die zugehörigen fundamentalen Ideen zu vertreten.

Die dazu seit den 1960er Jahren in Gang gesetzte Forschung führte zu vielfältigen Vorschlägen fundamentaler Ideen der Mathematik – jedoch bisher nicht zu einem allgemeingültigen Katalog. Dieser Vielfalt in den Formulierungen und Kategorisierungen kann begegnet werden, indem fundamentale Ideen über Eigenschaften charakterisiert werden. Schwill (1994) schlägt hierzu vor:

Definition 3.1 (Fundamentale Ideen) Eine fundamentale Idee bzgl. eines Gegenstandsbereichs (Wissenschaft, Teilgebiet) ist ein Denk-, Handlungs-, Beschreibungs- oder Erklärungsschema, das

1. in verschiedenen Gebieten des Bereichs vielfältig anwendbar oder erkennbar ist (Horizontalkriterium),
2. auf jedem intellektuellen Niveau aufgezeigt und vermittelt werden kann (Vertikalkriterium),
3. in der historischen Entwicklung des Bereichs deutlich wahrnehmbar ist und längerfristig relevant bleibt (Zeitkriterium),
4. einen Bezug zu Sprache und Denken des Alltags und der Lebenswelt besitzt (Sinnkriterium).

Fundamentale Ideen haben zwar ihren Ursprung in der Fachstruktur, aber sie »sind nicht Elemente der Wissenschaft an sich, sondern Produkte unseres Verstandes, die wir der Wissenschaft aufprägen. Folglich können sie nur relativ zum Menschen objektiviert werden« (Schubert & Schwill, 2011, S. 62).

Überblick zur historischen Entwicklung fundamentaler Ideen

• von der Bank (2016, 37 ff.): Fundamentale Ideen der Mathematik: Weiterentwicklung einer Theorie zu deren unterrichtspraktischer Nutzung

Für Ihre stoffdidaktische Analyse können fundamentale Ideen insbesondere hilfreich für die Dekonstruktion des Fachwissens und anschließende Rekonstruktion des Schulwissens sein.

Wenn sie also beispielsweise eine stoffdidaktische Analyse zur Flächeninhaltsberechnung durchführen, setzen Sie sich mit der fundamentalen Idee des Messens auseinander. Dabei verstehen Sie Messvorgänge als Vergleiche zu einem Standardmaß (z. B. Kästchen auszählen), erkennen Zerlegungs- und Ergänzungsgleichheit als notwendige Prinzipien zur präziseren Beschreibung, sehen Dreiecke als bedeutsame Basisfiguren für Flächeninhaltsberechnungen an und haben den Blick für die Integralrechnung als verallgemeinerbare Methode zur Flächeninhaltsbestimmung krummliniger Figuren (vgl. Vohns, 2000, 98 ff.). Sie dekonstruieren (zerlegen) damit Ihr eigenes mathematisches Fachwissen.

Nun sind Sie in der Lage, das Wissen zur Flächeninhaltsberechnung für Schülerinnen und Schüler neu aufzubauen, also zu rekonstruieren und (unter Hinzunahme der Betrachtung von Grundvorstellungen und den restlichen Ebenen des Vier-Ebenen-Ansatzes) einen Lernpfad zu entwickeln. Im Zusammenhang mit der Integralrechnung kann dies z. B. heißen, dass Sie parallel zum Bilden von Ober- und Untersummen noch einmal eine krummlinig begrenzte Fläche durch Kästchen auszählen lassen – ggf. mit unterschiedlicher Feinheit und einer Abschätzung nach oben und nach unten. Die fundamentalen Ideen haben für Sie damit auch eine ordnende Funktion des Unterrichtsstoffes.

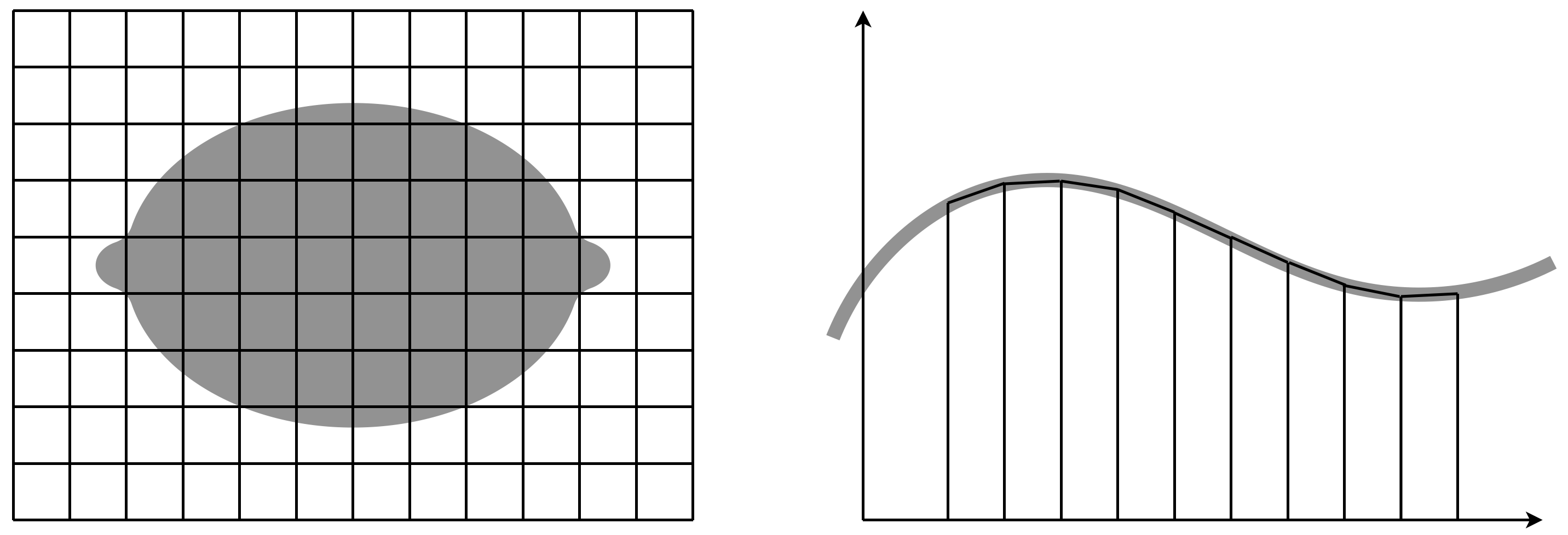
Abb. 3.1: Flächeninhaltsbestimmung

3.2.2 Auswahl fundamentaler Ideen

Das Fehlen eines allgemeingültigen Katalogs sollte nicht davon abhalten, bestehende Auflistungen und Strukturierungen fundamentaler Ideen zu betrachten. von der Bank (2013, S. 103) und Lambert (2012) diskutieren eine Kategorisierung fundamentaler Ideen in drei Bereiche:

• Inhaltsideen beziehen sich auf konkrete Inhaltsbereiche der Mathematik, die die Kriterien fundamentaler Ideen erfüllen können. Nicht ganz zufällig spiegeln diese sich in den Leitideen der Bildungsstandards wider (siehe Abschnitt 2.3).

• Schnittstellenideen haben die Eigenschaft, dass durch sie die »Mathe(matik) wirkt« und »auch für andere Fächer in ihrer je spezifischen Weise relevant sind« (Lambert, 2012). Damit korrelieren sie mit den prozessbezogenen Kompetenzen der Bildungsstandards.

• Tätigkeitsideen beziehen sich insbesondere auf innermathematische Tätigkeiten, die sich über verschiedene Inhaltsbereiche hinweg zeigen. Lambert (2012) betont, dass es diese (über die Bildungsstandards hinaus) ebenfalls zu beachten gilt, wenn man einen reichhaltigen Mathematikunterricht bewirken möchte.

Beispiele derartiger Tätigkeitsideen sind:

• Approximierung
• Optimierung
• Linearität/Linearisierung
• Symmetrie
• Invarianz
• Rekursion
• Vernetzung
• Ordnen
• Strukturierung
• Formalisierung
• Exaktifizierung
• Verallgemeinern
• Idealisieren

Im Rahmen des Projektmoduls Erweitertes Fachwissen für den schulischen Kontext in Mathematik⁸ werden Sie insbesondere Bezüge zwischen Schul- und Hochschulmathematik auf Basis fundamentaler Ideen herstellen, wofür die Inhalts- und Tätigkeitsideen von hoher Relevanz sind.

3.2.3 Beispiel Linearität

Horizontal- und Vertikalkriterium

Linearität ist ein wesentliches Konzept über die gesamte Schullaufbahn hinweg (und darüber hinaus). Dies spiegelt sich in vielfältigen Themenbereichen wider, die sowohl die Breite (Horizontalkriterium) als auch Tiefe (Vertikalkriterium) von Linearität und (später) auch Linearisierung zeigen. Dieser Abschnitt orientiert sich an den Darstellungen von Danckwerts (1988).

• Linearität als Phänomen tritt schon im Geometrieunterricht der Grundschule mit Geraden als essentielle geometrische Objekte auf. In der euklidischen Geometrie sind Geraden neben Punkten die Basisobjekte eines axiomatischen Aufbaus.
• Das Distributivgesetz \(a\cdot (b+c) = a\cdot b + a\cdot c\), das ebenfalls bereits in der Grundschule behandelt wird, beschreibt einen linearen Vorgang und bietet die Grundlage für die halbschriftliche Multiplikation. Über die Schulmathematik hinaus dient es z. B. als eines der Vektorraumaxiome (Skalarmultiplikation).
• Das Bestimmen eines Rechteckflächeninhalts ist ein linearer Vorgang: Ein Rechteck, das doppelt so breit ist, hat (bei gleicher Höhe) einen doppelt so großen Flächeninhalt. Betrachtet man diese Eigenschaft nicht als Phänomen, sondern als Forderung an eine Flächeninhaltsformel, so kann aus den Bedingungen \(A(a_1+a_2,b) = A(a_1,b) + A(a_2,b)\) und \(A(a,b_1+b_2) = A(a,b_1)+A(a,b_2)\) sowie der Stetigkeit in \(\mathbb{R}^+\) die Formel \(A(a,b) = a\cdot b\) abgeleitet werden.
• Lineare Zuordnungen der Art \(f(x+y) = f(x)+f(y)\) werden zu Beginn der Sekundarstufe I als proportionale Zuordnungen behandelt. Dies wird fortgeführt bei linearen Funktionen der Art \(f(x) = mx+n\), in der Fachmathematik als affin-lineare Abbildungen bezeichnet.
• Lineare Gleichungen und Gleichungssysteme sind ebenfalls bedeutsamer Bestandteil des Mathematikunterrichts. Überhaupt baut die gesamte Lineare Algebra auf lineare und affin-lineare Abbildungen auf.
• Die Strahlensätze beschreiben ebenfalls ein lineares Verhalten: Geradenabschnitte in \(c\)-facher Entfernung sind \(c\) mal so lang.

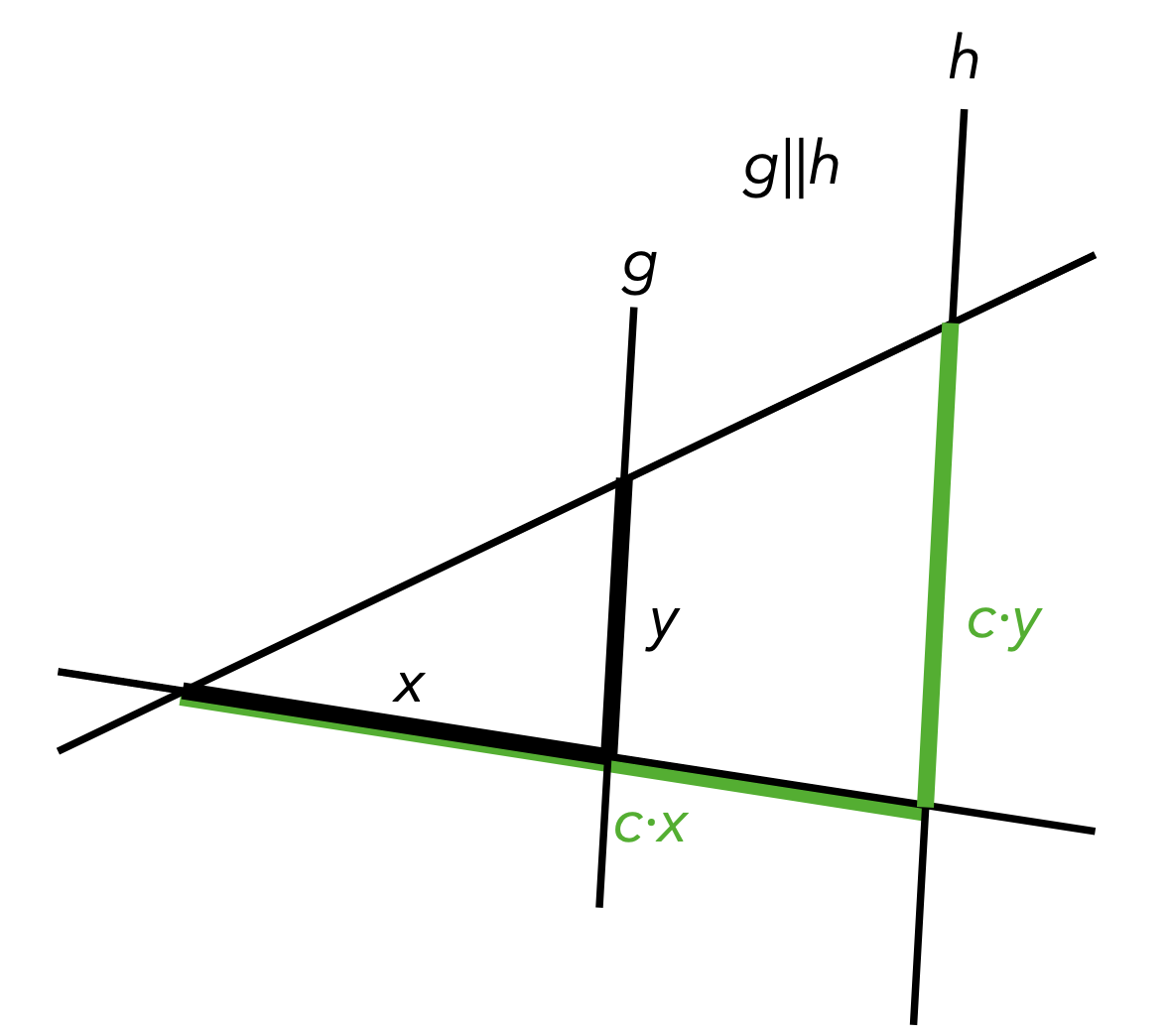
Abb. 3.2: Strahlensatzfigur

• Beim Ableitungsbegriff ist eine wesentliche Vorstellung, dass die Funktion in der Umgebung der zu betrachtenden Stelle linearisiert wird. Insbesondere bei höherdimensionalen Funktionen wird der Linearisierungsansatz weiterverfolgt. Die ebenfalls vorherrschende Tangentenvorstellung ist auf mehr als drei Dimensionen nicht mehr anschaulich übertragbar – der Linearisierungsansatz weist hier aufgrund seiner algebraischen Beschreibung die bessere Verallgemeinerbarkeit auf.
• Eng an den Linearisierungsansatz angelehnt ist die lineare Approximation von Funktionen (z. B. \(\sin(x)\approx x\) für \(x\approx 0\)). Die führt sich in der Hochschulmathematik fort, beispielsweise bei Taylor-Reihen.
• Das Bedürfnis der Linearisierung, insbesondere aus der Physik heraus, zeigt sich auch bei der Nutzung spezifisch skalierter Diagrammachsen, z. B. von Logarithmuspapier. Wegen der Äquivalenz von \(y = c\cdot a^x\) und \(\ln y = (\ln a )\cdot x + \ln c\) lassen sich beliebige Exponentialfunktionen auf Logarithmuspapier als lineare Funktionen darstellen.
• Verschiedene Näherungsverfahren, wie das Newton-Verfahren, bedienen sich ebenfalls der Linearisierung.

An dieser Stelle sei darauf hingewiesen, dass Linearität derart fundamental ist, dass selbst nicht-lineare Zusammenhänge häufig fälschlicherweise als linear angenommen werden. Dies zeigt sich zum Beispiel an den Fehlannahmen \((x+y)^2 \overset{?!}{=} x^2+y^2\), \(\sqrt{x+y} \overset{?!}{=} \sqrt{x}+\sqrt{y}\) oder \(\sin(x+y) \overset{?!}{=} \sin(x)+\sin(y)\). Derartige Fehler können Sie als Lehrkraft besser einordnen (und korrigieren), wenn Sie sich der fundamentalen Idee Linearität (die hier eben nicht gilt) bewusst sind. Insbesondere spricht dies auch für ein Explizitmachen der fundamentalen Idee Ihren Schülerinnen und Schülern gegenüber, so dass Sie derartigen Fehlern nicht nur mit Gegenbeispielen entgegen treten können, sondern auch eine strukturelle Einordnung sichtbar machen können.

Gerade wegen der genannten Fehlannahmen und der für die Schülerinnen und Schüler i. d. R. nicht in Zusammenhang gebrachten Dualität aus geradlinig und additiv und homogen sehen Tietze et al. (2002, S. 39) die Linearität dagegen nicht als eine im Mathematikunterricht etablierte fundamentale Idee, »die die Schüler erkennen und die ihr Denken ordnet und anregt«.

Zeit- und Sinnkriterium

Linearität zeigt sich auch in der historischen Entwicklung der Mathematik als eine prägende Leitlinie, womit sie das Zeitkriterium fundamentaler Ideen erfüllt. In der Linearen Algebra sei beispielsweise das Lösen linearer Gleichungssysteme im 18. Jahrhundert bis hin zum Gauß-Algorithmus im 19. Jahrhundert oder die Darstellung linearer Vorgänge mit Matrizen im 17./18. Jahrhundert erwähnt (vgl. Tietze et al., 2000b, 73 ff.). In der Analysis spiegelt sich die Linearität bzw. Linearisierung in der gesamten Differenzialrechnung wider, von der Interpolation nach der Jahrtausendwende über Taylors Linear perspective von 1715 (vgl. Brückler, 2018, 39,119) bis in die Gegenwart der linearen Modellierung nichtlinearer Zusammenhänge.

Historische Originalausgabe

Taylor (1715): Linear perspective

Auch Alltagssituationen bzw. die Alltagssprache ist von Linearität geprägt. Beispielsweise treten proportionale Zuordnungen unmittelbar beim Einkaufen auf, wenn Waren abgewogen und der Preis bestimmt wird. Auch reale Messvorgänge, wie z. B. die Geschwindigkeitsmessung, beziehen sich in der Regel auf die Messung von (sehr kurzen) Zeitintervallen, in denen ein lineares Verhalten angenommen wird. Das Sinnkriterium zeigt sich aber auch in Begriffen wie lineares Fernsehen oder lineare Erzählungen. Dies ist zwar keine mathematische Linearität im Sinne der Formel \(f(x+y) = f(x) +f(y)\), aber der Begriff findet in einer verwandten Bedeutung in der Alltagssprache Verwendung.

3.2.4 Gegenbeispiele

Zur Verständnisförderung sollen noch ein paar Gegenbeispiele für fundamentale Ideen angebracht werden.

• Das bereits erwähnte Distributivgesetz an sich ist zwar elementar, aber ihm fehlt die Weite, womit es nicht das Horizontalkriterium erfüllt. Die Linearität als dahinterliegende Idee ist dagegen weit genug (vgl. ähnliche Argumentation zum Kommutativgesetz und der dahinterliegenden Idee der Invarianz bei Schubert & Schwill, 2011, S. 63).
• Der Umkehrfunktion fehlt das Sinnkriterium, da dieser Begriff in der Lebenswelt außerhab der Mathematik kaum von Relevanz ist. Dahinter liegt vielmehr die Idee der Reversibilität als »Umkehrbarkeit von Operationen mit Wiederherstellung des Ausgangszustandes« (Schubert & Schwill, 2011, S. 63).

3.3 Grundvorstellungen

3.3.1 Begriffsklärung

Als Sie zu Beginn Ihres Mathematikstudiums die Peano-Axiome zur Definition der natürlichen Zahlen \(\mathbb{N}\) kennengelernt haben, konnten Sie dies wahrscheinlich – trotz der Neuigkeit der formalen Beschreibung – derart mit Ihrer Lebenswelterfahrung in Verbindung bringen, dass natürliche Zahlen abgezählt werden können, also dass damit z. B. die Platzierungen eines Wettrennens durchnummeriert werden können.

Peano-Axiome (Wikipedia, 2021a)

1. \(0\) ist eine natürliche Zahl.
2. Jede natürliche Zahl \(n\) hat eine natürliche Zahl \(n'\) als Nachfolger.
3. \(0\) ist kein Nachfolger einer natürlichen Zahl.
4. Natürliche Zahlen mit gleichem Nachfolger sind gleich.
5. Enthält die Menge \(X\) die \(0\) und mit jeder natürlichen Zahl \(n\) auch deren Nachfolger \(n'\), so bilden die natürlichen Zahlen eine Teilmenge von \(X\).

Dieser Bezug auf eine bekannte Handlung ist wesentlich dafür, dass die Definition und damit der Begriff der natürlichen Zahlen für Sie mit einem Sinn behaftet ist. Innerhalb dieser ordinalen Sichtweise natürlicher Zahlen helfen nun geeignete⁹ Repräsentationen dabei, sich Rechenoperationen vorstellen und sie operativ¹⁰ auszuführen zu können, also bspw. das Addieren als ein Weiterzählen aufzufassen (siehe Abbildung 3.3).

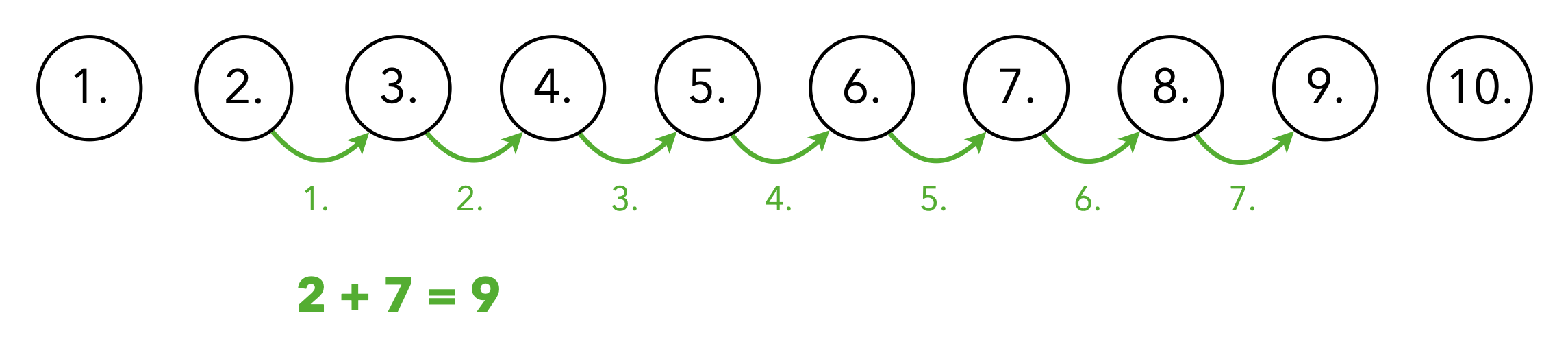
Abb. 3.3: Additionsaufgabe im ordinalen Zahlaspekt

Mit der Fähigkeit der Verknüpfung des mathematischen Begriffs und der Lebenswelt ist also eine Anwendung des Begriffs auf die Wirklichkeit möglich, insbesondere in Modellierungsprozessen. Dabei sind beide Richtungen relevant: Von der Realsituation zur Mathematik und von der Mathematik zur Realität.

Ziel des Mathematikunterrichts sollte es nun sein, für alle relevanten mathematischen Begriffe ein derartiges Verständnis aufzubauen, was auch heißt, verschiedene Vorstellungen zu einem Begriff zu vermitteln. Nach vom Hofe (1995, 97 f., Hervorhebung durch H.E.) ergibt sich daraus eine Orientierung an Grundvorstellungen im Mathematikunterricht:

Definition 3.2 (Grundvorstellungen) Die Grundvorstellungsidee beschreibt Beziehungen zwischen mathematischen Inhalten und dem Phänomen der individuellen Begriffsbildung. In ihren unterschiedlichen Ausprägungen charakterisiert sie mit jeweils unterschiedlichen Schwerpunkten insbesondere drei Aspekte dieses Phänomens:

• Sinnkonstituierung eines Begriffs durch Anknüpfung an bekannte Sach- oder Handlungszusammenhänge bzw. Handlungsvorstellungen,
• Aufbau entsprechender (visueller) Repräsentationen bzw. »Verinnerlichungen«, die operatives Handeln auf der Vorstellungsebene ermöglichen,
• Fähigkeit zur Anwendung eines Begriffs auf die Wirklichkeit durch Erkennen der entsprechenden Struktur in Sachzusammenhängen oder durch Modellieren des Sachproblems mit Hilfe der mathematischen Struktur.

3.3.2 Ausdifferenzierung

Weiterhin unterscheidet vom Hofe (2014) zwischen primären und sekundären Grundvorstellungen, abhängig von der Erfahrungswelt der Handlungen. Während sich primäre Grundvorstellungen auf reale Handlungserfahrungen stützen (z. B. mit Steckwürfeln in der Arithmetik), entstammen sekundäre Grundvorstellungen aus den Handlungen mit bereits im Mathematikunterricht aufgebauten Repräsentationen (z. B. Operationen auf dem Zahlenstrahl).

Entsprechend ihrer Definition werden Grundvorstellungen für Begriffe erarbeitet – hinsichtlich der Stoffelementkategorien (vgl. Abschnitt 2.4) also anscheinend nicht für Zusammenhänge und Verfahren. Jedoch können Grundvorstellungen zu einem Begriff sowohl hinsichtlich des Objekts an sich bestehen, als auch hinsichtlich der Operationen mit diesem Begriff. Das Addieren ist beispielsweise im Ordinalzahlaspekt eine Operation, verbunden mit der Grundvorstellung des Weiterzählens. Insofern können auch Zusammenhänge und Verfahren durchaus mit Grundvorstellungen verknüpft werden, sofern der Fokus auf dem Operieren mit den in ihnen enthaltenen Begriffen liegt.

Die in Definition 3.2 dargestellte Grundvorstellungsidee hat einen normativen Charakter, d. h. es wird davon ausgegangen, dass (aus professioneller Sicht der Mathematikdidaktik) zu mathematischen Begriffen bestimmte Grundvorstellungen identifiziert werden können, die es im Unterricht zu vermitteln gilt. Oder anders gefragt: »Welche Grundvorstellungen sind zur Lösung des Problems aus der Sicht des Lehrenden adäquat?« (vom Hofe, 1995, S. 106). Diese Sichtweise wird durch eine deskriptive Perspektive ergänzt: »Welche individuellen Vorstellungen lassen sich im Lösungsversuch des Schülers erkennen?« (vom Hofe, 1995, S. 107). Diese über empirische Untersuchungen zu ermittelnden Vorstellungen sind das, was sich Schülerinnen und Schüler tatsächlich unter einem Begriff vorstellen, wozu ggf. auch typische Fehlvorstellungen¹¹ gehören können. Kenntnisse darüber sind für Lehrkräfte ungemein wichtig, um Ergebnisse von Schülerinnen und Schülern interpretieren und einordnen zu können und dann ggf. entsprechende Hilfsangebote zu machen. Dies entspricht dann einer konstruktiven Perspektive auf Grundvorstellungen: »Worauf sind etwaige Divergenzen zurückzuführen, und wie lassen sich diese beheben?« (vom Hofe, 1995, S. 107).

Einige Quellen unterscheiden zwischen Aspekten und Grundvorstellungen. Nach Greefrath et al. (2016, S. 17) ist ein »Aspekt eines mathematischen Begriffs […] ein Teilbereich des Begriffs, mit dem dieser fachlich charakterisiert werden kann«, während »eine Grundvorstellung zu einem mathematischen Begriff […] eine inhaltliche Deutung des Begriffs [ist], die diesem Sinn gibt.« Im oben angebrachte Beispiel entspräche die Definition der natürlichen Zahlen über die Peano-Axiome dem Ordinalzahlaspekt, der mit der Grundvorstellung verbunden ist, dass die natürlichen Zahlen mit \(0\) beginnend eine feste Reihenfolge beschreiben. Da jedoch nicht alle Quellen diese Unterscheidung so präzise vornehmen und es auch teils zu Vermischungen kommt, soll diese (auf theoretischer Ebene relevante) Diskussion hier in der Stoffdidaktik-Veranstaltung nicht weiter von Relevanz sein. Für Ihre Unterrichtsgestaltung ist insbesondere relevant, dass sie einen aspektreichen bzw. an vielfältigen Grundvorstellungen orientierten Umgang mit Begriffen anstreben. Auch wenn Sie nicht unmittelbar und sofort jeweils alle Aspekte eines Begriffs im Unterricht ansprechen werden, hilft Ihnen das Wissen über den Aspektreichtum in der Unterrichtsplanung für die Ausbildung eines umfassenden Begriffsverständnisses.

3.3.3 GV und Stoffdidaktik

Im Rahmen dieser Veranstaltung, insbesondere den von Ihnen ausgearbeiteten Seminarthemen, wird der Schwerpunkt auf normative Grundvorstellungen gelegt, was der semantischen Ebene des Vier-Ebenen-Ansatzes zugeordnet werden kann, weil die mathematischen Begriffe hier mit einem Sinn versehen werden. Die deskriptive und konstruktive Perspektive sind dagegen der empirischen Ebene zuzuordnen, da hier individuelle Vorstellungen der Schülerinnen und Schüler von Relevanz sind. Dies betrifft insbesondere auch das Potenzial, (ggf. mathematisch unvollständige) individuelle Vorstellungen aufzugreifen bei der Ausbildung von (normativ erwünschten) Grundvorstellungen.

Das Identifizieren von Grundvorstellungen zu einem Begriff ist, genau wie bei den fundamentalen Ideen, Aufgabe der mathematikdidaktischen Forschung (ein Modell dafür findet man z. B. bei Salle & Clüver, 2021). Als Lehrkraft profitieren Sie von diesen Ergebnissen und nutzen sie für Ihre stoffdidaktische Analyse.

Im Gegensatz zu den fundamentalen Ideen, die ihren Ursprung in der Sachstruktur des mathematischen Inhalts haben, fokussieren die Grundvorstellungen stärker auf den Sinn des fachlichen Begriffs für das Individuum. Grundvorstellungen beziehen sich auf spezifische Begriffe und Operationen mit Begriffen, während fundamentale Ideen größere, themenübergreifende Leitlinien für die Stoffauswahl und -strukturierung bilden.

Für die Unterrichtsplanung und -durchführung ist neben der Frage, welche Grundvorstellungen von Relevanz sind (Spezifizieren im Vier-Ebenen-Ansatz) vor allem interessant, wie diese ausgebildet werden können (Strukturieren im Vier-Ebenen-Ansatz). Letzteres wird u. a. in den nächsten Kapiteln näher beleuchtet.

3.3.4 Beispiele

3.3.4.1 Natürliche Zahlen

Betrachten Sie folgenden (fiktiven) Zeitungsartikel:

Harlequin erneut auf dem 1. Platz

Bei dem traditionellen Pferderennen am 15. Mai hat das Pferd Harlequin erneut gewonnen. Unter den 10 Pferden, die an den Start gingen, belegte es mit 21,3 Sekunden den 1. Platz. Damit war es fast 2 mal so schnell unterwegs wie das letzte Pferd, das ins Ziel kam. Karten für das nächste Rennen können unter 030 23125143 bestellt werden.

In dem Text tauchen Zahlen unter vielen Aspekten auf: Der 1. Platz und 15. Mai sind Ordinalzahlen, also Zahlen, die eine Ordnung beschreiben. Wie oben schon beschrieben, lassen diese sich fachmathematisch über die Peano-Axiome beschreiben und wenn mit ihnen gerechnet, entspricht z. B. das Addieren dem Weiterzählen.

Die 10 Pferde stellen eine Kardinalzahl dar, also die Anzahl der Elemente einer Menge. Addiert man Kardinalzahlen, so müssen Mengen vereinigt werden, z. B. anschaulich, indem man sie zusammen legt.

Die 21,3 Sekunden entsprechen einer Maßzahl, da diese Zahl die Funktion hat, etwas auszumessen (hier die Zeit). Das Addieren in diesem Aspekt entspräche dem Aneinanderlegen, z. B. wenn zwei Längenangaben addiert werden.

Dass es 2 mal so schnell wird, enspricht einem Operatoraspekt, mit dem die Vielfachheit eines Vorganges beschrieben wird. Das Addieren ist hierin eine Hinereinanderausführung eines Vorganges.

Die Telefonnumer 030 23125143 wiederum erfüllt einen Codierungsaspekt. Sie hat im mathematischen Sinne keine Bedeutung, nur die Anordnung der Ziffern ist von Relevanz. Entsprechend kann innerhalb dieses Aspektes auch nicht addiert werden. Weitere Beispiele hierfür wären Postleitzahlen oder Identifikationsnummern.

Hinzu kommt noch der Aspekt der Rechenzahl. Informationen dazu sowie eine genauere Erläuterung der Zahlaspekte und damit verbundenen Operationen findet man z. B. bei Krauthausen (2018, 43 ff.).

3.3.4.2 Bruchzahlen

Nachdem die Schülerinnen und Schüler ihr gesamte Vorschul- und Primarstufenzeit mit Natürlichen Zahlen verbracht haben, treten mit der Einführung von Bruchzahlen Umbrüche in den subjektiven Vorstellungen auf. Zum Beispiel sind folgende (vermeintlichen) Gesetzmäßigkeiten plötzlich nicht mehr gültig:

• Das Produkt zweier Zahlen ist größer als die jeweiligen Faktoren.
• Die Multiplikation kann als wiederholte Addition aufgefasst werden.
• Jede Zahl hat genau einen Repräsentanten.
• Je mehr Stellen eine Zahl hat, desto größer ist sie.

Die Bruchzahlen selbst besitzen nach Padberg & Wartha (2017, 19 ff.) folgende Aspekte:

• Bruch als Anteil eines Ganzen oder mehrerer Ganzer (z. B. \(\frac{2}{3}\) als zwei Drittel einer Pizza oder je ein Drittel von zwei Pizzen),
• Bruch als Maßzahl (z. B. \(\frac{1}{4}\) Liter),
• Bruch als Operator (z. B. \(\frac{1}{5}\) von 250 €),
• Bruch als Verhältnis (z. B. \(\frac{2}{3}\) mit der Bedeutung 2 von 3 Schüler/-innen tragen eine Brille),
• Bruch als Quotient (z. B. \(\frac{3}{5}\) als Ergebnis bzw. andere Schreibweise von \(3:5\)),
• Bruch als Lösung einer linearen Gleichung (z. B. \(\frac{3}{5}\) als Lösung von \(5x = 3\)),
• Bruch als Skalenwert (z. B. \(\frac{3}{2}\) als Mitte zwischen \(1\) und \(2\) auf dem Zahlenstrahl),
• Quasikardinale Auffassung von Brüchen (z. B. \(\frac{3}{5}\) als 3 mal \(\frac{1}{5}\)).

Neben den Grundrechenoperationen führt auch das Vergleichen von Brüchen zu Grundvorstellungsumbrüchen. Hinzu kommen noch besondere Operationen mit Bruchzahlen wie das Erweitern und Kürzen.

Das Multiplizieren von Brüchen kann bspw. als Anteilsbildung (\(\frac{1}{5}\) mal … heißt \(\frac{1}{5}\) von …) oder als Rechteckfläche aufgefasst werden (Padberg & Wartha, 2017, 108 ff), siehe Abbildung 3.4.

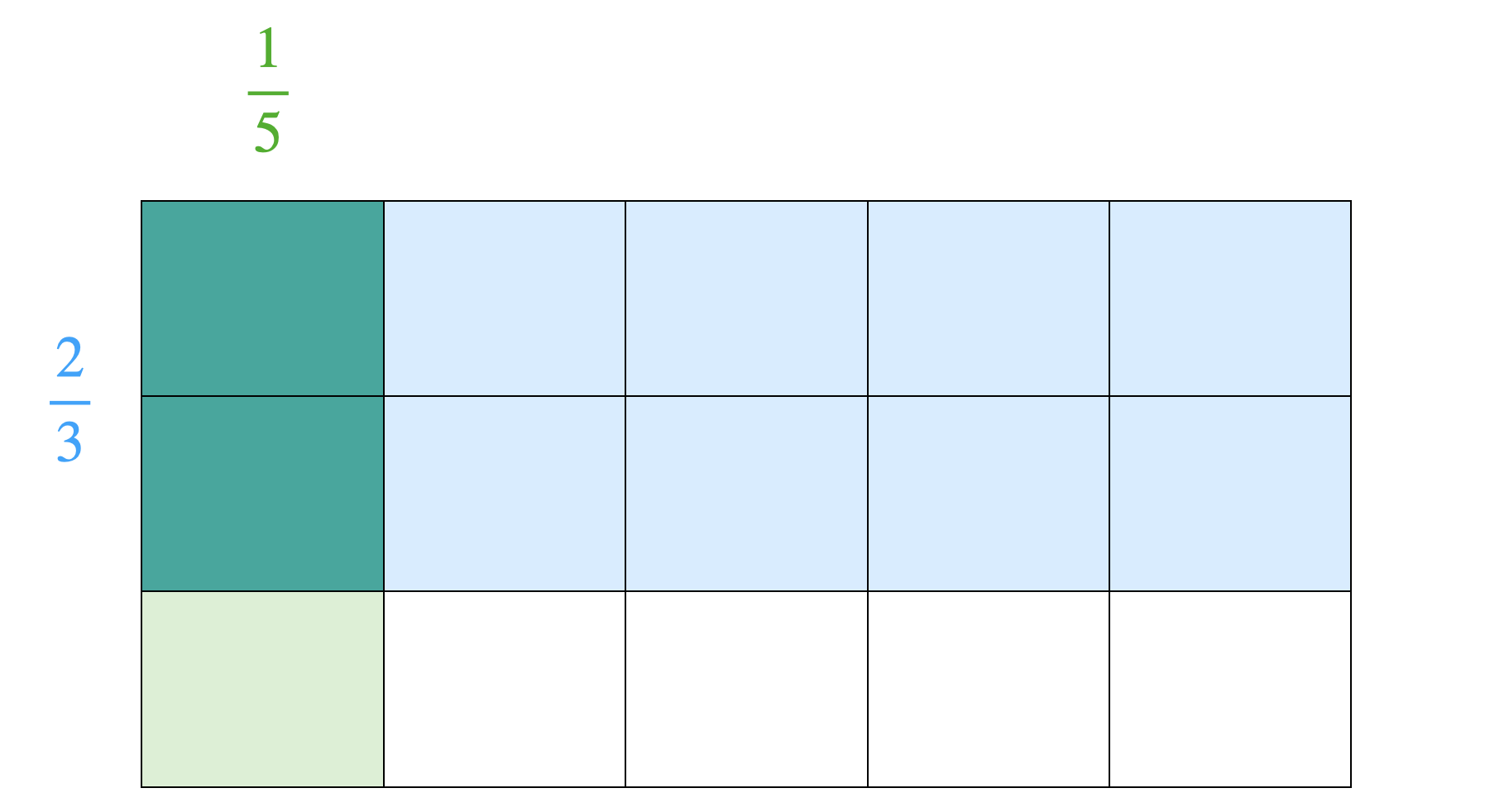
Abb. 3.4: Vorstellung von \(\frac{1}{5} \cdot \frac{2}{3}\) als Rechteckfläche

All dies zeigt, dass Brüche behutsam unterrichtet werden sollten und von einer rein kalkülorientierten Behandlung unbedingt abgesehen werden muss, da diese den nachhaltigen Lernerfolg deutlich mindert.

3.3.4.3 Negative Zahlen

Aufbauend auf die in Abschnitt 2.5 erfolgte Diskussion zur formalen Ebene von negativen Zahlen, soll zu diesen nun die Grundvorstellungsidee auf der semantischen Ebene diskutiert werden.

Die Einführung negativer Zahlen ist für Schülerinnen und Schüler mit zahlreichen Schwierigkeiten verbunden (vom Hofe & Hattermann, 2014). Diese sind eigentlich auf der empirischen Ebene der stoffdidaktischen Analyse angesiedelt, sollen aber hier wegen ihrer Nähe zu den Grundvorstellungen schon einmal erwähnt werden.

• So bestehen etwa für das Minus-Zeichen vielfältige Interpretationsmöglichkeiten als Vorzeichen (z. B. in der Rechnung \(-5+2\)), als Rechenzeichen (z. B. in der Rechnung \(7-2\)) oder als Inversionszeichen (z. B. bei der Darstellung \(-a\) als Gegenzahl für \(a\)).
• Der in den natürlichen Zahlen vorhandene Kardinalzahlaspekt (dass die Zahl die Mächtigkeit einer Menge angibt), ist in den negativen Zahlen nicht mehr tragfähig (es existiert keine \(-4\)-elementige Menge). Auch der Ordinalzahlaspekt (dass die Zahl eine Position angibt) ist nur eingeschränkt tragfähig (eine \(-4\)-te Position bedarf vielfältiger Zwischeninterpretationen). Der Maßzahlaspekt (z. B. über die Angabe einer Zahl auf dem Zahlenstrahl) dagegen ist auf die negativen Zahlen erweiterbar.
• Die Ordnungsrelation wird häufig fehlinterpretiert über eine spiegelbildliche Interpretation (z. B. kann fälschlicherweise \(-5>-3\) angenommen werden). Eine Ursache kann hier darin liegen, dass die Ordnungsrelation zuvor über die Mächtigkeit von Mengen hergestellt wurde, was nun nicht mehr möglich ist.

Gegenüber den natürlichen Zahlen sind also im Umgang mit negativen Zahlen einige Grundvorstellungsumbrüche zu absolvieren. Als normativ auszubildende Grundvorstellungen fassen vom Hofe & Hattermann (2014) für rationale Zahlen (als Obermenge positiver und negativer Zahlen) zusammen:

• Rationale Zahlen als relative Zahlen bezüglich einer fest gewählten Vergleichsmarke: Dies ist etwa bei Etagen-Angaben, Temperaturen oder der Position über/unter dem Wasserspiegel der Fall. Gerade bei Temperaturen kann die Beliebigkeit der Vergleichsmarke (0 °C) gut diskutiert werden, da etwa andere Temperaturskalen (°F, K) eine andere Vergleichsmarke gewählt haben.
• Rationale Zahlen als Gegensätze: Diese Vorstellung wird z. B. sichtbar, wenn über Guthaben und Schulden gesprochen wird. Hat man 5 € Schulden, so ist dies der Gegensatz von 5 € Guthaben. Die Vergleichsmarke (0 €) ist hier nicht beliebig gewählt, sondern natürlicherweise über »weder Guthaben noch Schulden« gegeben. Auch der Betrag einer Zahl kann in dieser Vorstellung besonders gut verstanden werden.
• Rationale Zahlen als Richtungen: Negative Zahlen beschreiben in dieser Vorstellung die entgegengesetzte Richtung der positiven Zahlen. Dies ist z. B. bei der Verwendung von Koordinatensystemen der Fall, oder ganz allgemein bei der Zahlengeraden.
• Rationale Zahlen als Zustände und Zustandsänderungen: In dieser Vorstellung bieten rationale Zahlen nicht nur die Möglichkeit, einen Zustand (wie Guthaben oder Schulden) zu beschreiben, sondern auch den Prozess der Änderung dieser Zustände (Erhalt von Guthaben, Erlass von Schulden, …). Eine solche Vorstellung etwa ist nötig, um die verschiedenen Interpretationen des Minus-Zeichens nachvollziehen zu können.

Als bedeutsamste Repräsentation negativer Zahlen gilt die Zahlengerade. Diese stützt einerseits den Maßzahlaspekt und ermöglicht über die Darstellung von Punkten und Pfeilen (siehe Abbildung 3.5) auch eine Interpretation in den verschiedenen Grundvorstellungen.

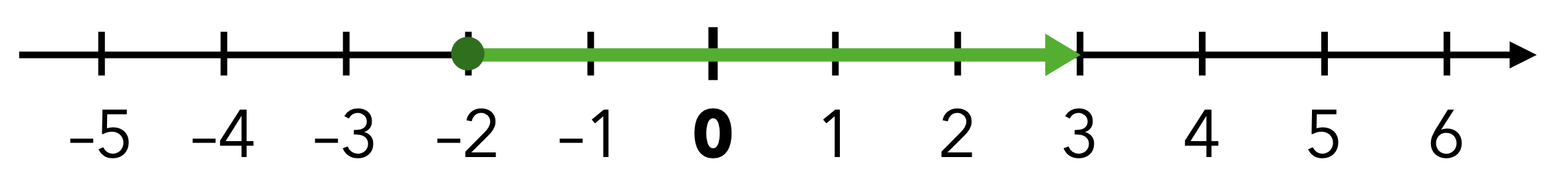
Abb. 3.5: Zahlengerade

Auch Operationen mit negativen Zahlen sind hierzu nun verständlich behandelbar:

• So kann das Addieren/Subtrahieren als Anlegen von Pfeilen, gerichtetes Weiter-/Zurückzählen oder als Subtraktion/Addition der Gegenzahl aufgefasst werden.
• Das Multiplizieren kann bei der Multiplikation mit einer positiven Zahl als Streckung/Stauchung aufgefasst werden, die Multiplikation mit \(-1\) entspricht der Spiegelung an der Null und die Multiplikation mit einer beliebigen negativen Zahl ist eine Kombination aus beidem.
• Der Größenvergleich ist nun über einen Lagevergleich auf der Zahlengeraden möglich, wobei weiter links liegende Zahlen immer kleiner sind als weiter rechts liegende.

Zusammenfassend lassen sich auf der semantischen Ebene folgende für den Lernpfad relevanten Aussagen ableiten:

• Rationale Zahlen sollten als relative Zahlen bezüglich einer fest gewählten Vergleichsmarke, als Gegensätze, als Richtungen sowie als Zustände und Zustandsänderungen aufgefasst werden können.
• Die Zahlengerade ist eine wesentliche Repräsentation rationaler Zahlen, anhand derer auch die Operationen mit rationalen Zahlen sichtbar gemacht werden können.

References

Brückler, F. M. (2018). Geschichte der Mathematik kompakt: Das Wichtigste aus Analysis, Wahrscheinlichkeitstheorie, angewandter Mathematik, Topologie und Mengenlehre. Springer Spektrum. https://doi.org/10.1007/978-3-662-55574-3

Bruder, R., Feldt-Caesar, N., Pallack, A., Pinkernell, G., & Wynands, A. (2015). Mathematisches Grundwissen und Grundkönnen in der Sekundarstufe II. In W. Blum, S. Vogel, C. Drüke-Noe, & A. Roppelt (Hrsg.), Bildungsstandards aktuell: Mathematik in der Sekundarstufe II (S. 108–124). Schroedel.

Bruner, J. S. (1976). Die Bedeutung der Struktur im Lernprozeß. In A. Holtmann (Hrsg.), Das sozialwissenschaftliche Curriculum in der Schule: Neue Formen und Inhalte (S. 77–90). VS Verlag für Sozialwissenschaften. https://doi.org/10.1007/978-3-322-85275-5

Danckwerts, R. (1988). Linearität als organisierendes Element zentraler Inhalte der Schulmathematik. Didaktik der Mathematik, 16(2), 149–160.

Feldt-Caesar, N. (2017). Konzeptualisierung und Diagnose von mathematischem Grundwissen und Grundkönnen. Springer Fachmedien Wiesbaden. https://doi.org/10.1007/978-3-658-17373-9

Greefrath, G., Oldenburg, R., Siller, H.-S., Ulm, V., & Weigand, H.-G. (2016). Didaktik der Analysis. Aspekte und Grundvorstellungen zentraler Begriffe (F. Padberg & A. Büchter, Hrsg.; 4. Aufl.). Springer Spektrum. https://doi.org/10.1007/978-3-662-48877-5

Krauthausen, G. (2018). Einführung in die Mathematikdidaktik (F. Padberg & A. Büchter, Hrsg.; Mathematik Primarstufe und Sekundarstufe I + II). Springer Spektrum. https://doi.org/10.1007/978-3-662-54692-5

Lambert, A. (2012). Gedanken zum aktuellen Kompetenzbegriff für den (Mathematik-)unterricht [Vortrag]. Eingangsstatement zur Podiumsdiskussion im Rahmen des 3. Fachdidaktischen Kolloquiums an der Universität des Saarlandes, Saarbrücken. https://www.uni-saarland.de/fileadmin/upload/einrichtung/zfl/PDF_Fachdidaktik/PDF_Kolloquium_FD/Kompetenzbegriff_für_den_Mathematikunterricht_Statement_mit_Folien.pdf

Padberg, F., & Wartha, S. (2017). Didaktik der Bruchrechnung (5. Aufl.). Springer Spektrum. https://doi.org/10.1007/978-3-662-52969-0

Salle, A., & Clüver, T. (2021). Herleitung von Grundvorstellungen als normative Leitlinien – Beschreibung eines theoriebasierten Verfahrensrahmens. Journal für Mathematik-Didaktik. https://doi.org/10.1007/s13138-021-00184-5

Schecker, H., Wilhelm, T., Hopf, M., & Duit, R. (Hrsg.). (2018). Schülervorstellungen und Physikunterricht: Ein Lehrbuch für Studium, Referendariat und Unterrichtspraxis. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-57270-2

Schubert, S., & Schwill, A. (2011). Didaktik der Informatik (2. Aufl). Spektrum, Akad. Verl. https://doi.org/10.1007/978-3-8274-2653-6

Schwill, A. (1994). Fundamentale Ideen in Mathematik und Informatik. Herbsttagung des Arbeitskreises Mathematikunterricht und Informatik, Wolfenbüttel. http://www.informatikdidaktik.de/didaktik/Forschung/Wolfenbuettel94.pdf

Taylor, B. (1715). Linear perspective. printed for R. Knaplock at the Bishop’s-Head in St. Paul’s Church-Yard. https://nl.sub.uni-goettingen.de/id/0590700700

Tietze, U.-P., Klika, M., & Wolpers, H. (Hrsg.). (2000b). Mathematikunterricht in der Sekundarstufe II. Band 2: Didaktik der Analytischen Geometrie und Linearen Algebra. Vieweg+Teubner Verlag. https://doi.org/10.1007/978-3-322-86479-6

Tietze, U.-P., Klika, M., & Wolpers, H. (Hrsg.). (2002). Mathematikunterricht in der Sekundarstufe II. Band 3: Didaktik der Stochastik. Vieweg+Teubner Verlag. https://doi.org/10.1007/978-3-322-83144-6

Vohns, A. (2000). Das Messen als fundamentale Idee [1. Staatsexamensarbeit, Universität-Gesamthochschule Siegen]. https://wwwu.aau.at/avohns/pdf/messen.pdf

vom Hofe, R. (1995). Grundvorstellungen mathematischer Inhalte. Spektrum Akademischer Verlag.

vom Hofe, R. (2014). Primäre und sekundäre Grundvorstellungen. In J. Roth & J. Ames (Hrsg.), Beiträge zum Mathematikunterricht 2014, 48. Jahrestagung der Gesellschaft für Didaktik der Mathematik vom 10.03.2014 bis 14.03.2014 in Koblenz. WTM. https://doi.org/10.17877/DE290R-8808

vom Hofe, R., & Hattermann, M. (2014). Zugänge zu negativen Zahlen. mathematik lehren, 2–7.

von der Bank, M.-C. (2013). Fundamentale Ideen, insbesondere Optimierung. In A. Filler & M. Ludwig (Hrsg.), Wege zur Begriffsbildung für den Geometrieunterricht. Ziele und Visionen 2020. Vorträge auf der 29. Herbsttagung des Arbeitskreises Geometrie in der Gesellschaft für Didaktik der Mathematik vom 14. bis 16. September 2012 in Saarbrücken (S. 83–124). Franzbecker. https://www.math.uni-sb.de/service/lehramt/AKGeometrie/AKGeometrie2012.pdf

von der Bank, M.-C. (2016). Fundamentale Ideen der Mathematik: Weiterentwicklung einer Theorie zu deren unterrichtspraktischer Nutzung [Dissertation, Universität des Saarlandes]. https://doi.org/10.22028/D291-26673

Wikipedia. (2021a). Peano-Axiome — Wikipedia, die freie Enzyklopädie. https://de.wikipedia.org/w/index.php?title=Peano-Axiome&oldid=216675163

---

7. Dargestellt sind bei Feldt-Caesar (2017, 124 f.) Zielperspektiven zur Auswahl von Lerngegenständen zur Ausbildung von Mindesstandards, aufbauend auf Arbeiten von Bruder et al. (2015). Die Grundgedanken wurdn hier übernommen und hinsichtlich der Bedeutung von Lerngegenständen angereichert.↩︎

8. siehe Modulbeschreibung zum Modul MAT-LS-7 bei PULS↩︎

9. Geeignet heißt in diesem Fall, dass sich die Kernaussage des Begriffs in der Repräsentation wiederfindet. Im Ordinalzahlaspekt ist dies v. a. die Reihung von Zahlen. Was dabei (noch) nicht relevant ist, ist zum Beispiel die exakte Messbarkeit, wie man sie etwa auf dem Zahlenstrahl repräsentiert.↩︎

10. Operativ heißt hier zum Beispiel, dass Sie zu einer Aufgabe wie \(2+7\) Nachbaraufgaben (\(2+8\)), Umkehraufgaben (\(7-2\)), Platzhalteraufgaben (\(2+\boxed{\phantom{5}}=7\)) usw. aufstellen und lösen können.↩︎

11. Mit Fehlvorstellungen sind hier individuelle Vorstellungen der Schülerinnen und Schüler gemeint, die mathematisch nicht tragfähig und daher aus fachlicher Perspektive fehlerhaft sind. So ist etwa die Vorstellung, dass Multiplizieren immer vergrößert, in den Natürlichen Zahlen tragfähig (und damit eine Grundvorstellung), in den Bruchzahlen jedoch nicht mehr tragfähig und wird dort dann zur Fehlvorstellung. Neben Fehlvorstellungen können weitere individuelle Vorstellungen Alltagsvorstellungen, Präkonzepte o. ä. sein (siehe auch Schecker et al., 2018, 11 f.).↩︎